Pour reporter l'angle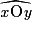 
:
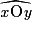:- On trace une demi-droite [O'x').
- Sur
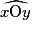, pointe sèche en O, on trace un arc de cercle qui coupe [Ox) en I et [Oy) en J. On reporte cet arc de cercle, pointe sèche en O' : il coupe [O'x') en I'.
 |
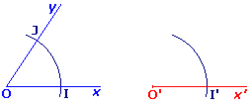- Avec un écartement IJ, pointe sèche en I', on trace un deuxième arc de cercle qui coupe le premier en J'.
- On joint O' à J' : on obtient [O'y'). On a :
 |
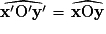
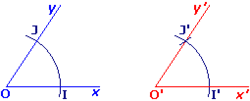Exercice n°1
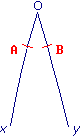
On veut reporter un angle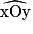 
.
. |
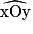Numérote les étapes de 1 à 4.
Remettez les étiquettes dans l'ordre en les glissant dans les zones prévues à cet effet.
Avec un écartement égal à AB, pointe sèche en A', on trace un deuxième arc qui coupe le premier en B'.
On reporte [Ox) : on obtient [O'x').
On joint O' à B' : c'est [O'y').
Sur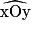 
, pointe sèche en O, on trace un arc de cercle qui coupe [Ox) en A et [Oy) en B. On reporte ce premier arc : il coupe [O'x') en A'.
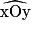, pointe sèche en O, on trace un arc de cercle qui coupe [Ox) en A et [Oy) en B. On reporte ce premier arc : il coupe [O'x') en A'. imcAnswer1?
imcAnswer2?
imcAnswer3?
imcAnswer4?
• Il faut commencer par reporter l'un des côtés de l'angle.
• On trace ensuite un arc de cercle qui permet de reporter son « ouverture ».
Exercice n°2
Imprime et utilise ton compas pour répondre.
 |
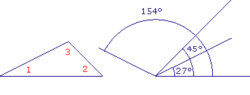L'angle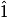 
mesure :
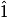mesure : Cochez la bonne réponse.
| ||
| ||
|
Exercice n°3
Coche la bonne réponse.
a. Pour reproduire un angle droit, il suffit de savoir construire une droite perpendiculaire à une autre.
Cochez la bonne réponse.
| ||
|
 |
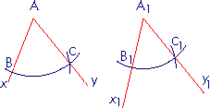b.
A-t-on correctement reproduit l'angle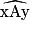 
en A1 ?
Imprime et vérifie à l'aide d'un compas avant de répondre.
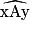en A1 ?Imprime et vérifie à l'aide d'un compas avant de répondre.
Cochez la bonne réponse.
| ||
|
a. Deux droites perpendiculaires forment un angle droit.
b. Pour reproduire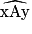 
au compas :
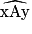au compas :- on trace la demi-droite [A1 x1) ;
- avec un écartement de compas égal à AB, pointe en A1, on trace un premier arc de cercle qui coupe [A1 x1) en B1 ;
- avec un écartement de compas égal à BC, pointe en B1, on trace un second arc de cercle qui coupe le premier en C1 ;
- on joint A1 et C1, l'angle obtenu est alors égal à
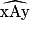. Ce qui n'est pas le cas ici.
