Lorsqu'une expression comporte plusieurs opérations, comme par exemple 2 + 4 × 4, on peut se demander s'il s'agit d'une somme ou d'un produit.
Méthode :
Pour savoir si une expression est une somme ou un produit, on regarde la dernière opération à effectuer en respectant les règles de priorités.
Règle de priorités :
On commence toujours par les calculs entre parenthèses, puis les puissances, les multiplications (ou les divisions) et on termine par les additions (ou soustractions).
Exemples :
Méthode :
Pour savoir si une expression est une somme ou un produit, on regarde la dernière opération à effectuer en respectant les règles de priorités.
Règle de priorités :
On commence toujours par les calculs entre parenthèses, puis les puissances, les multiplications (ou les divisions) et on termine par les additions (ou soustractions).
Exemples :
- 2 + 3 + 4 × 4 = 2 + 3 + 16 = 5 + 16
- La multiplication est prioritaire sur l'addition donc on calcule d'abord 4 × 4. Il reste donc la somme à faire. C'est une somme.
- ( 2 + 3 × 4) × (5 - 2) = (2 + 12) × (3) = 14 × 3
- Les parenthèses sont prioritaires ; quand on calcule l'intérieure de la première, la multiplication y est prioritaire. Ensuite l'addition à l'intérieure de la parenthèse est prioritaire sur la multiplication. Au final, il reste un produit.
Remarque :
Si l'addition est une somme, la soustraction est aussi considérée comme une somme (celle d'un nombre positif et un nombre négatif). Idem pour la division qui est considérée comme un produit (d'un nombre par l'inverse d'un autre).
Si l'addition est une somme, la soustraction est aussi considérée comme une somme (celle d'un nombre positif et un nombre négatif). Idem pour la division qui est considérée comme un produit (d'un nombre par l'inverse d'un autre).
- 2 × 4 − 25/5 = 8 − 5
- 2 × 4 et 25/5 sont prioritaires, il reste donc 8 - 5 qui est la dernière opération menée, il s'agit d'une soustraction donc d'une somme.
Exercice n°1
"une somme" ou "un produit" ? Complète les phrases.
L'expression : 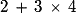 est .
est .
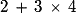 est .
est .L'expression (2 × 3 − 2 ) × 5 + 1 est .
L'expression 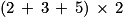 est .
est .
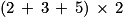 est .
est .Exercice n°2
Remplace les espaces vides par le signe mathématique approprié afin d'obtenir ce qui est demandé. (Il y a peut-être plusieurs solutions.)
L'expression : 2 × 4 5 × 6 est une somme.
L'expression : 2 × 5 3 est un produit.
2 × 4 + 5 × 6 = 8 + 30
La dernière opération à effectuer est une addition, l'expression est donc une somme.
2 × 4 − 5 × 6 = 8 − 30
La dernière opération à effectuer est une soustraction, l'expression est donc une somme.
La dernière opération à effectuer est une addition, l'expression est donc une somme.
2 × 4 − 5 × 6 = 8 − 30
La dernière opération à effectuer est une soustraction, l'expression est donc une somme.
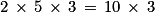
La dernière opération à effectuer est une multiplication, l'expression est donc un produit.
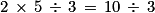
La dernière opération à effectuer est une division, l'expression est donc un produit.
Exercice n°3
Place les parenthèses au bon endroit afin d'obtenir ce qui est demandé. Attention : il ne faut placer qu'un seul couple de parenthèses.
L'expression : 2 + 3 × 5 est un produit.
L'expression : 2 + 3 × 5 est une somme.
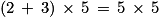 .
.La dernière opération à effectuer est une multiplication, donc l'expression est un produit.
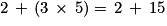 .
.La dernière opération à effectuer est une addition, donc l'expression est une somme.

