Propriété générale
Quels que soient les points A, B et C, on a : AB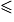 
AC + BC.
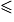AC + BC.• Situation 1 : AB = AC + BC
Le point C appartient alors au segment [AB].
Le point C appartient alors au segment [AB].
 |
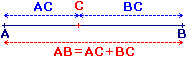• Situation 2 : AB < AC + BC
Le point C est alors en dehors du segment [AB].
Le point C est alors en dehors du segment [AB].
Conditions d'existence d'un triangle
Si a, b et c sont les longueurs des côtés d'un triangle, alors :
a < b + c
b < a + c
c < a + b
a < b + c
b < a + c
c < a + b
 |
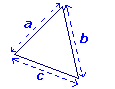• Étant donnés trois nombres a, b et c, on ne peut construire un triangle dont les côtés ont pour mesures ces nombres que si a, b, c vérifient les inégalités ci-dessus.
• Ainsi, si a = 15, b = 5 et c = 8, la construction du triangle est impossible car 15 > 5 + 8.
Exercice n°1
On veut construire trois points A, B et C définis par la mesure des longueurs AB, AC et BC.
Associe à chaque cas le commentaire qui convient.
Associe à chaque cas le commentaire qui convient.
Faites glisser les étiquettes dans les zones prévues à cet effet.
A, B et C sont alignés.
ABC est un triangle.
c'est impossible
1. AB = 2 ; AC = 4 ; BC = 7.
→ Réponse :
→ Réponse :
imcAnswer1?
. 2. AB = 12,5 ; AC = 4,9 ; BC = 7,8.
→ Réponse :
→ Réponse :
imcAnswer2?
. 3. AB = 4,9 ; AC = 3,6 ; BC = 1,3.
→ Réponse :
→ Réponse :
imcAnswer3?
. 1. 2 + 4 = 6
Comme BC = 7,8 alors BC > AB + AC.
La construction est impossible.
Comme BC = 7,8 alors BC > AB + AC.
La construction est impossible.
2. 4,9 + 7,8 = 12,7
Comme AB = 12,5, alors AB < AC + BC.
Comme AB = 12,5, alors AB < AC + BC.
3. 3,6 + 1,3 = 4,9
A, C et B sont alignés dans cet ordre.
A, C et B sont alignés dans cet ordre.
Exercice n°2
Soit les points A, B, C et D tels que :
CD = 4,2 ; AC = 1,7 ; AB = 8,5 ; AD = 5,9 ; BC = 10,2.
CD = 4,2 ; AC = 1,7 ; AB = 8,5 ; AD = 5,9 ; BC = 10,2.
Complète.
Écrivez les réponses dans les zones colorées.
1. Sur [BC] se trouve le point .
2. Sur [AD] se trouve le point .
3. A, B, C, D sont donc .
1. 10,2 = 8,5 + 1,7
BC = BA + AC, donc A est entre B et C.
BC = BA + AC, donc A est entre B et C.
2. 5,9 = 1,7 + 4,2
AD = AC + CD, donc C est entre A et D.
AD = AC + CD, donc C est entre A et D.
3. B appartient à (AC) et D appartient à (AC).
Exercice n°3
Coche les réponses exactes.
1. Si l'on choisit trois dimensions au hasard, on peut construire un triangle :
Cochez la bonne réponse.
| ||
| ||
|
2. On peut construire un triangle de côtés :
Cochez la bonne réponse.
| ||
| ||
|
On ne peut construire un triangle que si chacun de ses côtés a une mesure inférieure à la somme des mesures des deux autres côtés.
Exercice n°4
A, B et C sont trois points distincts.
Calcule la longueur manquante.
Calcule la longueur manquante.
Écrivez les réponses dans les zones colorées.
a. A, B et C sont alignés dans cet ordre ; AB = 3 cm ; BC = 7 cm ; AC = cm.
b. A, B et C sont alignés dans cet ordre ; AC = 8 cm ; BC = 5 cm ; AB = cm.
c. B, C et A sont alignés dans cet ordre ; AC = 8 cm ; BC = 5 cm ; AB = cm.
d. C, A et B sont alignés dans cet ordre ; AB = 4 cm ; BC = 9 cm ; CA = cm.
Tu peux faire des dessins si tu as des difficultés à imaginer la figure.
a. AC = 3 + 7 = 10 (cm).
b. AB = AC − BC = 8 − 5 = 3 (cm).
c. AB = 8 + 5 = 13 (cm).
d. CA = CB − AB = 9 − 4 = 5 (cm).
Exercice n°5
Dans chacun des cas suivants, est-il possible de construire un triangle ayant pour longueur de ses côtés les dimensions données ?
Coche la bonne réponse.
Coche la bonne réponse.
a. Dimensions du triangle : 3 cm ; 2 cm ; 4 cm.
Cochez la bonne réponse.
| ||
|
b. Dimensions du triangle : 7 cm ; 10 cm ; 8 cm.
Cochez la bonne réponse.
| ||
|
c. Dimensions du triangle : 1,5 cm ; 3,5 cm ; 6 cm.
Cochez la bonne réponse.
| ||
|
d. Dimensions du triangle : 12 cm ; 23 cm ; 10 cm.
Cochez la bonne réponse.
| ||
|
a. Oui car :
3 − 2 < 4 < 3 + 2
4 − 2 < 3 < 4 + 2
4 − 3 < 2 < 4 + 3
3 − 2 < 4 < 3 + 2
4 − 2 < 3 < 4 + 2
4 − 3 < 2 < 4 + 3
b. Oui car :
8 − 7 < 10 < 8 + 7
10 − 8 < 7 < 10 + 8
10 − 7 < 8 < 10 + 7
8 − 7 < 10 < 8 + 7
10 − 8 < 7 < 10 + 8
10 − 7 < 8 < 10 + 7
c. Impossible car :
3,5 − 1,5 = 2
3,5 + 1,5 = 5
Or 6 n'est pas compris entre 2 et 5.
3,5 − 1,5 = 2
3,5 + 1,5 = 5
Or 6 n'est pas compris entre 2 et 5.
d. Impossible car :
12 + 10 = 22
12 − 10 = 2
Or 23 n'est pas compris entre 2 et 22.
12 + 10 = 22
12 − 10 = 2
Or 23 n'est pas compris entre 2 et 22.
Exercice n°6
On te donne les dimensions de deux des côtés d'un triangle.
Entre quelles valeurs doit être compris le troisième côté du triangle ?
Entre quelles valeurs doit être compris le troisième côté du triangle ?
Écrivez les réponses dans les zones colorées.
a. 2,5 cm ; 2 cm ; 3e côté entre cm et cm.
b. 8 cm ; 3 cm ; 3e côté entre cm et cm.
c. 5 cm ; 7,3 cm ; 3e côté entre cm et cm.
a. 2,5 − 2 < 3e côté < 2,5 + 2
D'où 0,5 < 3e côté < 4,5.
D'où 0,5 < 3e côté < 4,5.
b. 8 − 3 < 3e côté < 8 + 3
D'où 5 < 3e côté < 11.
D'où 5 < 3e côté < 11.
c. 7,3 − 5 < 3e côté < 7,3 + 5
D'où 2,3 < 3e côté < 12,3.
D'où 2,3 < 3e côté < 12,3.
