Nouveau message
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2016, exercice 4
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2016, exercice 4
Signaler une erreur
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2016, exercice 4
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2016, exercice 4
Imprimer
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2016, exercice 4
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2016, exercice 4
Énoncé
5 points
Lors des soldes, un commerçant décide d'appliquer une réduction de 30 % sur l'ensemble des articles de son magasin.
1.
L'un des articles coûte 54 € avant la réduction. Calculer son prix après la réduction.
Quel est le coefficient multiplicateur associé à une réduction de 30 % ?
2.
Le commerçant utilise la feuille de calcul ci-dessous pour calculer les prix des articles soldés.
 |
a)
Pour calculer la réduction, quelle formule a-t-il pu saisir dans la cellule B2 avant de l'étirer sur la ligne 2 ?
Comment calcule-t-on le montant de la réduction de 30 % à partir du prix avant réduction ?
b)
Pour obtenir le prix soldé, quelle formule peut-il saisir dans la cellule B3 avant de l'étirer sur la ligne 3 ?
Comment calcule-t-on le prix soldé à partir du montant avant réduction et de la réduction ?
3.
Le prix soldé d'un article est 42,00 €. Quel était son prix initial ?
Notez x le prix initial de l'article dont le prix soldé est 42,00 € et résolvez une équation simple.
Corrigé
1. Le coefficient multiplicateur associé à une réduction de 30 % est :
1 −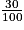
= 1 − 0,3 = 0,7.
Le prix d'un article coûtant 54 € avant la réduction de 30 % est donc 0,7 × 54 = 37,80 € après réduction.
1 −
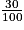= 1 − 0,3 = 0,7.Le prix d'un article coûtant 54 € avant la réduction de 30 % est donc 0,7 × 54 = 37,80 € après réduction.
2.
a) Pour calculer le montant de la réduction de 30 % à partir du prix avant réduction, on multiplie ce prix par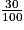 
= 0,3.
Pour calculer la réduction, la formule saisie dans la cellule B2, qui est étirée ensuite sur la ligne 2, est donc : « = 0,3*B1 ».
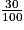= 0,3.Pour calculer la réduction, la formule saisie dans la cellule B2, qui est étirée ensuite sur la ligne 2, est donc : « = 0,3*B1 ».
b) Le prix soldé est la différence entre le prix avant réduction et le montant de la réduction.
Pour calculer le prix soldé, la formule saisie dans la cellule B3, qui est étirée ensuite sur la ligne 3, est donc : « =B1 − B2 ».
Pour calculer le prix soldé, la formule saisie dans la cellule B3, qui est étirée ensuite sur la ligne 3, est donc : « =B1 − B2 ».
Remarque : le prix soldé étant égal au prix avant réduction multiplié par 0,7, on peut aussi saisir dans la cellule B3 la formule : « = 0,7*B1 ».
3. Notons x le prix initial de l'article dont le prix soldé est 42,00 €.
En fonction de x, le prix de l'article après la réduction de 30 % est 0,7 × x = 0,7x.
On a donc 0,7x = 42, puis x =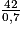
= 60 €.
Le prix initial d'un article dont le prix soldé est 42,00 € est 60,00 €.
En fonction de x, le prix de l'article après la réduction de 30 % est 0,7 × x = 0,7x.
On a donc 0,7x = 42, puis x =
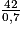= 60 €.Le prix initial d'un article dont le prix soldé est 42,00 € est 60,00 €.
Corrigé
1. Le coefficient multiplicateur associé à une réduction de 30 % est :
1 −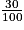 = 1 − 0,3 = 0,7.
Le prix d'un article coûtant 54 € avant la réduction de 30 % est donc 0,7 × 54 = 37,80 € après réduction.
1 −
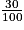= 1 − 0,3 = 0,7.Le prix d'un article coûtant 54 € avant la réduction de 30 % est donc 0,7 × 54 = 37,80 € après réduction.
2.
a) Pour calculer le montant de la réduction de 30 % à partir du prix avant réduction, on multiplie ce prix par 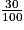= 0,3.
Pour calculer la réduction, la formule saisie dans la cellule B2, qui est étirée ensuite sur la ligne 2, est donc : « = 0,3*B1 ».
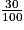= 0,3.Pour calculer la réduction, la formule saisie dans la cellule B2, qui est étirée ensuite sur la ligne 2, est donc : « = 0,3*B1 ».
b) Le prix soldé est la différence entre le prix avant réduction et le montant de la réduction.
Pour calculer le prix soldé, la formule saisie dans la cellule B3, qui est étirée ensuite sur la ligne 3, est donc : « =B1 − B2 ».
Pour calculer le prix soldé, la formule saisie dans la cellule B3, qui est étirée ensuite sur la ligne 3, est donc : « =B1 − B2 ».
Remarque : le prix soldé étant égal au prix avant réduction multiplié par 0,7, on peut aussi saisir dans la cellule B3 la formule : « = 0,7*B1 ».
3. Notons x le prix initial de l'article dont le prix soldé est 42,00 €.
En fonction de x, le prix de l'article après la réduction de 30 % est 0,7 × x = 0,7x.
On a donc 0,7x = 42, puis x =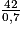 = 60 €.
Le prix initial d'un article dont le prix soldé est 42,00 € est 60,00 €.
En fonction de x, le prix de l'article après la réduction de 30 % est 0,7 × x = 0,7x.
On a donc 0,7x = 42, puis x =
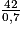= 60 €.Le prix initial d'un article dont le prix soldé est 42,00 € est 60,00 €.
Nouveau message
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2016, exercice 4
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2016, exercice 4
Signaler une erreur
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2016, exercice 4
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2016, exercice 4
Imprimer
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2016, exercice 4
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2016, exercice 4
