Énoncé
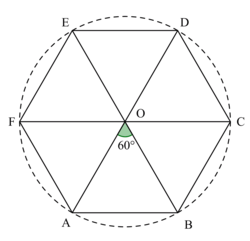
ABCDEF est un hexagone régulier de centre O. C'est-à-dire que :
- AB = BC = CD = DE = EF = FA ;
- OA = OB = OC = OD = OE = OF ;
 =
= 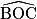 =
= 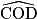 =
= 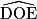 =
= 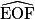 =
=  =
= 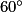 .
.
 |
1.
Quelle est l'image du point B par la translation définie par les points O et C ?
Vous devez trouver le point X tel que OCXA soit un parallélogramme.
2.
Quelle est l'image du point A par la translation définie par les points C et D ?
Vous devez trouver le point Y tel que CDYA soit un parallélogramme.
3.
Quelle est l'image du point C par la rotation de centre O, d'angle 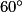 dans le sens des aiguilles d'une montre ?
dans le sens des aiguilles d'une montre ?
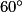 dans le sens des aiguilles d'une montre ?
dans le sens des aiguilles d'une montre ?Faites attention au sens de la rotation.
4.
Quelle est l'image du triangle OCD par la rotation de centre O, d'angle 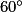 dans le sens des aiguilles d'une montre ?
dans le sens des aiguilles d'une montre ?
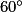 dans le sens des aiguilles d'une montre ?
dans le sens des aiguilles d'une montre ?Déterminez aussi l'image du point D par la rotation de centre O, d'angle 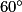 dans le sens des aiguilles d'une montre.
dans le sens des aiguilles d'une montre.
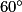 dans le sens des aiguilles d'une montre.
dans le sens des aiguilles d'une montre.5.
Quelle est l'image du point E par la rotation de centre O, d'angle 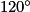 dans le sens inverse des aiguilles d'une montre ?
dans le sens inverse des aiguilles d'une montre ?
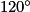 dans le sens inverse des aiguilles d'une montre ?
dans le sens inverse des aiguilles d'une montre ?Faites attention au sens de la rotation.
6.
Quelle est l'image du triangle EFO par la rotation de centre O, d'angle 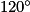 dans le sens inverse des aiguilles d'une montre ?
dans le sens inverse des aiguilles d'une montre ?
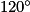 dans le sens inverse des aiguilles d'une montre ?
dans le sens inverse des aiguilles d'une montre ?Déterminez aussi l'image du point F par la rotation de centre O, d'angle 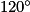 dans le sens inverse des aiguilles d'une montre.
dans le sens inverse des aiguilles d'une montre.
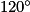 dans le sens inverse des aiguilles d'une montre.
dans le sens inverse des aiguilles d'une montre.Corrigé
1.
L'image du point A par la translation définie par les points O et C est le point X tel que le quadrilatère OCXA soit un parallélogramme.
OA = CB et OC = AB donc le quadrilatère OCBA est un parallélogramme.
L'image du point A par la translation définie par les points O et C est donc le point B.
OA = CB et OC = AB donc le quadrilatère OCBA est un parallélogramme.
L'image du point A par la translation définie par les points O et C est donc le point B.
2.
L'image du point A par la translation définie par les points C et D est le point X tel que le quadrilatère CDXA soit un parallélogramme.
CD = AF et AC = FD car ABCO et DEFO sont des losanges de mêmes dimensions et superposables, donc le quadrilatère CDFA est un parallélogramme.
L'image du point A par la translation définie par les points C et D est donc le point F.
CD = AF et AC = FD car ABCO et DEFO sont des losanges de mêmes dimensions et superposables, donc le quadrilatère CDFA est un parallélogramme.
L'image du point A par la translation définie par les points C et D est donc le point F.
3.
On a 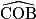 =
= 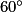 .
.
L'image du point C par la rotation de centre O, d'angle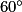 dans le sens des aiguilles d'une montre est donc le point B.
dans le sens des aiguilles d'une montre est donc le point B.
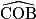 =
= 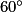 .
.L'image du point C par la rotation de centre O, d'angle
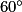 dans le sens des aiguilles d'une montre est donc le point B.
dans le sens des aiguilles d'une montre est donc le point B.4.
De même, on a 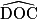 =
= 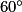 .
.
L'image du point D par la rotation de centre O, d'angle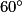 dans le sens des aiguilles d'une montre est donc le point C.
dans le sens des aiguilles d'une montre est donc le point C.
L'image du point O par cette rotation étant le point O, l'image du triangle OCD par cette rotation est le triangle OBC.
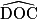 =
= 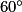 .
.L'image du point D par la rotation de centre O, d'angle
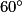 dans le sens des aiguilles d'une montre est donc le point C.
dans le sens des aiguilles d'une montre est donc le point C.L'image du point O par cette rotation étant le point O, l'image du triangle OCD par cette rotation est le triangle OBC.
5.
On a  =
= 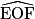 +
+  =
= 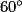 +
+ 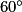 =
= 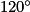 .
.
L'image du point E par la rotation de centre O, d'angle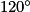 dans le sens inverse des aiguilles d'une montre est donc le point A.
dans le sens inverse des aiguilles d'une montre est donc le point A.
 =
= 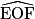 +
+  =
= 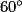 +
+ 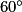 =
= 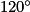 .
.L'image du point E par la rotation de centre O, d'angle
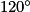 dans le sens inverse des aiguilles d'une montre est donc le point A.
dans le sens inverse des aiguilles d'une montre est donc le point A.6.
De même, on a  =
=  +
+  =
= 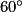 +
+ 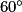 =
= 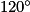 .
.
L'image du point F par la rotation de centre O, d'angle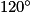 dans le sens inverse des aiguilles d'une montre est donc le point B.
dans le sens inverse des aiguilles d'une montre est donc le point B.
L'image du point O par cette rotation étant le point O, l'image du triangle EFO par cette rotation est le triangle ABO.
 =
=  +
+  =
= 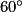 +
+ 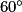 =
= 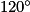 .
.L'image du point F par la rotation de centre O, d'angle
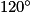 dans le sens inverse des aiguilles d'une montre est donc le point B.
dans le sens inverse des aiguilles d'une montre est donc le point B.L'image du point O par cette rotation étant le point O, l'image du triangle EFO par cette rotation est le triangle ABO.

