Signaler une erreur
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2015, exercice 7
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2015, exercice 7
Imprimer
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2015, exercice 7
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2015, exercice 7
Énoncé
4 points
Ce panneau routier indique une descente dont la pente est de 10 %.
 |
Cela signifie que pour un déplacement horizontal de 100 mètres, le dénivelé est de 10 mètres.
Le schéma ci-dessous n'est pas à l'échelle.
Le schéma ci-dessous n'est pas à l'échelle.
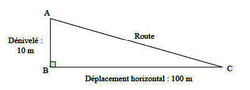 |
1. Déterminer la mesure de l'angle 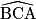 que fait la route avec l'horizontale. Arrondir la réponse au degré.
que fait la route avec l'horizontale. Arrondir la réponse au degré.
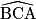 que fait la route avec l'horizontale. Arrondir la réponse au degré.
que fait la route avec l'horizontale. Arrondir la réponse au degré.Utilisez une relation trigonométrique dans le triangle ABC rectangle en B. Vous devez trouver un angle compris entre 5 et 10°.
2. Dans certains pays, il arrive parfois que la pente d'une route ne soit pas donnée par un pourcentage, mais par une indication telle que « 1 : 5 », ce qui veut alors dire que pour un déplacement horizontal de 5 mètres, le dénivelé est de 1 mètre.
Lequel des deux panneaux ci-dessous indique la pente la plus forte ?
Lequel des deux panneaux ci-dessous indique la pente la plus forte ?
 |
Pour les descentes représentées par les deux panneaux, déterminez le pourcentage de pente le plus élevé.
Corrigé
1.
Dans le triangle ABC rectangle en B, on a :
tan (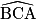 ) =
) = 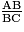 =
= 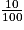 = 0,1.
= 0,1.
En utilisant la calculatrice (en mode degré) :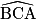 = tan−1(0,1)
= tan−1(0,1) 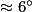 au degré près.
au degré près.
tan (
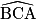 ) =
) = 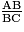 =
= 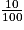 = 0,1.
= 0,1.En utilisant la calculatrice (en mode degré) :
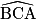 = tan−1(0,1)
= tan−1(0,1) 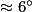 au degré près.
au degré près.2.
Pour le panneau A, la pente est de 15 % et, pour le panneau B, la pente est de 100 × 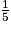 = 20 %.
= 20 %.
C'est donc le panneau B qui indique la pente la plus forte.
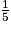 = 20 %.
= 20 %. C'est donc le panneau B qui indique la pente la plus forte.
Corrigé
1.
Dans le triangle ABC rectangle en B, on a :
tan (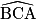 ) =
) = 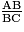 =
= 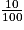 = 0,1.
= 0,1.
En utilisant la calculatrice (en mode degré) :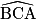 = tan−1(0,1)
= tan−1(0,1) 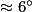 au degré près.
au degré près.
tan (
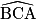 ) =
) = 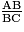 =
= 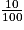 = 0,1.
= 0,1.En utilisant la calculatrice (en mode degré) :
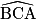 = tan−1(0,1)
= tan−1(0,1) 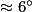 au degré près.
au degré près.2.
Pour le panneau A, la pente est de 15 % et, pour le panneau B, la pente est de 100 × 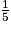 = 20 %.
= 20 %.
C'est donc le panneau B qui indique la pente la plus forte.
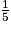 = 20 %.
= 20 %. C'est donc le panneau B qui indique la pente la plus forte.
Signaler une erreur
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2015, exercice 7
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2015, exercice 7
Imprimer
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2015, exercice 7
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2015, exercice 7

