Signaler une erreur
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2015, exercice 3
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2015, exercice 3
Imprimer
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2015, exercice 3
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2015, exercice 3
Énoncé
4 points
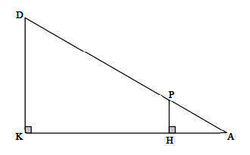
Dans la figure ci-après, qui n'est pas à l'échelle :
- les points D, P et A sont alignés ;
- les points K, H et A sont alignés ;
- DA = 60 cm ;
- DK = 11 cm ;
- DP = 45 cm.
 |
1.
Calculer KA au millième près.
Appliquez le théorème de Pythagore dans le triangle DKA rectangle en K.
2.
Calculer HP.
Montrez que les droites (DK) et (HP) sont parallèles et appliquez le théorème de Thalès dans le triangle DKA.
Corrigé
1.
Dans le triangle DKA rectangle en K, d'après le théorème de Pythagore, on a :
DA2 = KD2 + KA2 donc KA2 = DA2 − KD2 = 602 − 112 = 3 600 − 121 = 3 479.
KA > 0 donc KA =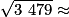 59,0 au millimètres près.
59,0 au millimètres près.
DA2 = KD2 + KA2 donc KA2 = DA2 − KD2 = 602 − 112 = 3 600 − 121 = 3 479.
KA > 0 donc KA =
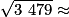 59,0 au millimètres près.
59,0 au millimètres près. Remarque :
L'écriture 59,0 signifie que le résultat est arrondi au dixième près de centimètres (c'est-à-dire au millimètre près). Même si c'est le même résultat, l'écriture 59 signifierait que le résultat est arrondi à l'unité près.
L'écriture 59,0 signifie que le résultat est arrondi au dixième près de centimètres (c'est-à-dire au millimètre près). Même si c'est le même résultat, l'écriture 59 signifierait que le résultat est arrondi à l'unité près.
2.
Montrons que les droites (DK) et (HP) sont parallèles.
Les droites (DK) et (HP) sont perpendiculaires à la même droite (KH) donc elles sont parallèles entre elles.
En effet, si deux droites sont perpendiculaires à une même droite, alors elles sont parallèles entres elles.
Les droites (DK) et (HP) sont perpendiculaires à la même droite (KH) donc elles sont parallèles entre elles.
En effet, si deux droites sont perpendiculaires à une même droite, alors elles sont parallèles entres elles.
Dans le triangle DKA, les points D, P et A d'une part, et les points K, H et A d'autre part sont alignés.
Les droites (DK) et (HP) sont parallèles donc, d'après le théorème de Thalès :
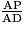 =
= 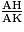 =
= 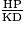 et en particulier
et en particulier 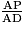 =
= 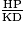 .
.
On a donc AP × KD = HP × AD, puis 15 × 11 = 60 × HP, car AP = DA − DP = 60 − 45 = 15 cm, et 60 × HP = 165.
Finalement, HP =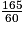 = 2,75 cm.
= 2,75 cm.
Les droites (DK) et (HP) sont parallèles donc, d'après le théorème de Thalès :
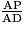 =
= 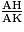 =
= 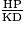 et en particulier
et en particulier 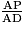 =
= 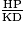 .
. On a donc AP × KD = HP × AD, puis 15 × 11 = 60 × HP, car AP = DA − DP = 60 − 45 = 15 cm, et 60 × HP = 165.
Finalement, HP =
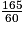 = 2,75 cm.
= 2,75 cm.Corrigé
1.
Dans le triangle DKA rectangle en K, d'après le théorème de Pythagore, on a :
DA2 = KD2 + KA2 donc KA2 = DA2 − KD2 = 602 − 112 = 3 600 − 121 = 3 479.
KA > 0 donc KA =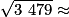 59,0 au millimètres près.
59,0 au millimètres près.
DA2 = KD2 + KA2 donc KA2 = DA2 − KD2 = 602 − 112 = 3 600 − 121 = 3 479.
KA > 0 donc KA =
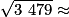 59,0 au millimètres près.
59,0 au millimètres près. Remarque :
L'écriture 59,0 signifie que le résultat est arrondi au dixième près de centimètres (c'est-à-dire au millimètre près). Même si c'est le même résultat, l'écriture 59 signifierait que le résultat est arrondi à l'unité près.
L'écriture 59,0 signifie que le résultat est arrondi au dixième près de centimètres (c'est-à-dire au millimètre près). Même si c'est le même résultat, l'écriture 59 signifierait que le résultat est arrondi à l'unité près.
2.
Montrons que les droites (DK) et (HP) sont parallèles.
Les droites (DK) et (HP) sont perpendiculaires à la même droite (KH) donc elles sont parallèles entre elles.
En effet, si deux droites sont perpendiculaires à une même droite, alors elles sont parallèles entres elles.
Les droites (DK) et (HP) sont perpendiculaires à la même droite (KH) donc elles sont parallèles entre elles.
En effet, si deux droites sont perpendiculaires à une même droite, alors elles sont parallèles entres elles.
Dans le triangle DKA, les points D, P et A d'une part, et les points K, H et A d'autre part sont alignés.
Les droites (DK) et (HP) sont parallèles donc, d'après le théorème de Thalès :
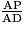 =
= 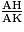 =
= 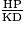 et en particulier
et en particulier 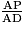 =
= 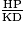 .
.
On a donc AP × KD = HP × AD, puis 15 × 11 = 60 × HP, car AP = DA − DP = 60 − 45 = 15 cm, et 60 × HP = 165.
Finalement, HP =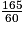 = 2,75 cm.
= 2,75 cm.
Les droites (DK) et (HP) sont parallèles donc, d'après le théorème de Thalès :
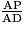 =
= 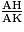 =
= 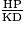 et en particulier
et en particulier 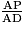 =
= 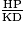 .
. On a donc AP × KD = HP × AD, puis 15 × 11 = 60 × HP, car AP = DA − DP = 60 − 45 = 15 cm, et 60 × HP = 165.
Finalement, HP =
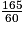 = 2,75 cm.
= 2,75 cm.
Signaler une erreur
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2015, exercice 3
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2015, exercice 3
Imprimer
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2015, exercice 3
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2015, exercice 3

