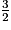Si on connaît deux côtés d'un triangle rectangle, on peut calculer la mesure des trois angles.
Soit ABC un triangle rectangle en A.
On donne : [AB] = 7 et [AC] = 5.
On veut calculer la mesure des angles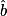 et
et 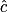 .
.
Ici, on connaît [AC], le côté opposé à l'angle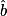 et [AB], le côté adjacent à l'angle
et [AB], le côté adjacent à l'angle 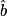 .
.
On va donc utiliser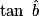 pour calculer
pour calculer 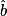 .
.
On donne : [AB] = 7 et [AC] = 5.
On veut calculer la mesure des angles
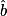 et
et 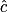 .
.Ici, on connaît [AC], le côté opposé à l'angle
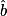 et [AB], le côté adjacent à l'angle
et [AB], le côté adjacent à l'angle 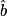 .
.On va donc utiliser
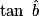 pour calculer
pour calculer 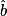 .
. |
• Calcul de  :
:
On a :![\mathbf{\tan~\hat{\textit{b}}~=~\frac{[AC]}{[AB]}~=~\frac{5}{7}}](https://static1.assistancescolaire.com/3/images/3mtr07_m8.png) .
.
On obtient la valeur de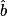 en utilisant la fonction inv tan de la calculatrice.
en utilisant la fonction inv tan de la calculatrice.
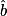 = 35° (à un degré près par défaut).
= 35° (à un degré près par défaut).
 :
:On a :
![\mathbf{\tan~\hat{\textit{b}}~=~\frac{[AC]}{[AB]}~=~\frac{5}{7}}](https://static1.assistancescolaire.com/3/images/3mtr07_m8.png) .
.On obtient la valeur de
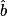 en utilisant la fonction inv tan de la calculatrice.
en utilisant la fonction inv tan de la calculatrice. = 35° (à un degré près par défaut).
= 35° (à un degré près par défaut).• Calcul de 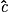 :
:
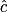 = 90° – 35° car la somme des angles d'un triangle est 180°.
= 90° – 35° car la somme des angles d'un triangle est 180°.
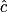 = 55°
= 55°
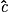 :
: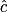 = 90° – 35° car la somme des angles d'un triangle est 180°.
= 90° – 35° car la somme des angles d'un triangle est 180°.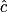 = 55°
= 55°Exercice n°1
ABC est un triangle rectangle en A. Coche la réponse qui convient.
1. On connaît AB et AC ; pour calculer 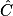 , on utilise son cosinus.
, on utilise son cosinus.
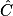 , on utilise son cosinus.
, on utilise son cosinus. Cochez la bonne réponse.
| ||
|
2. On connaît AB et BC ; pour calculer 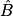 , on utilise son cosinus.
, on utilise son cosinus.
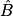 , on utilise son cosinus.
, on utilise son cosinus. Cochez la bonne réponse.
| ||
|
3. On connaît AC et BC ; pour calculer 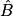 , on utilise son cosinus.
, on utilise son cosinus.
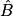 , on utilise son cosinus.
, on utilise son cosinus. Cochez la bonne réponse.
| ||
|
1. On ne peut pas utiliser le cosinus de 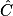 car on ne connaît pas l'hypoténuse.
car on ne connaît pas l'hypoténuse.
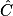 car on ne connaît pas l'hypoténuse.
car on ne connaît pas l'hypoténuse.Exercice n°2
Soit un triangle MNP rectangle en M.
On donne : MN = 6 et NP = 10.
On veut calculer la mesure de l'angle.
On donne : MN = 6 et NP = 10.
On veut calculer la mesure de l'angle.
Complète le raisonnement.
Écrivez les réponses dans les zones colorées.
1. On connaît la longueur MN du côté à l'angle 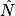 et la longueur NP de l'.
et la longueur NP de l'.
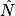 et la longueur NP de l'.
et la longueur NP de l'. 2. On va donc utiliser de l'angle 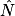 .
.
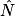 =
= 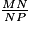 ; d'où
; d'où 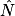 = ° (arrondi à l'unité).
= ° (arrondi à l'unité).
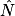 .
.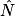 =
= 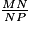 ; d'où
; d'où 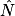 = ° (arrondi à l'unité).
= ° (arrondi à l'unité). 1. On connaît le côté adjacent à l'angle 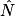 et l'hypoténuse. Il faut donc utiliser le cosinus de l'angle
et l'hypoténuse. Il faut donc utiliser le cosinus de l'angle 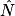 .
.
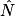 et l'hypoténuse. Il faut donc utiliser le cosinus de l'angle
et l'hypoténuse. Il faut donc utiliser le cosinus de l'angle 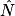 .
. 2. cos 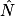 =
= 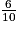 = 0,6.
= 0,6.
Vérifie que ta calculatrice est en mode DEG et tape 0,6 INV COS =.
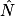 =
= 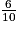 = 0,6.
= 0,6.Vérifie que ta calculatrice est en mode DEG et tape 0,6 INV COS =.
Exercice n°3
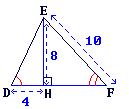 |
DH = 4
EH = 8
EF = 10
EH = 8
EF = 10
Donne une valeur arrondie au dixième des angles suivants.
Écrivez les réponses dans les zones colorées.
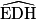 = °.
= °.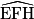 = °.
= °.Dans le triangle rectangle EDH, tu connais EH et DH.
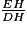 = tan
= tan 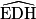 d'où tan
d'où tan 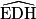 =
= 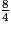 = 2.
= 2.
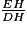 = tan
= tan 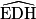 d'où tan
d'où tan 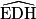 =
= 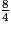 = 2.
= 2. Dans le triangle rectangle EFH, tu connais EH et EF.
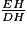 = sin
= sin 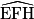 d'où sin
d'où sin 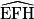 =
= 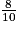 = 0,8.
= 0,8.
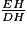 = sin
= sin 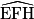 d'où sin
d'où sin 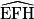 =
= 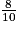 = 0,8.
= 0,8.Exercice n°4
Complète les réponses suivantes (l'unité de longueur est le cm).
Écrivez les réponses dans les zones colorées.
a. ABC est un triangle rectangle en B tel que AC = 3 et BC = 2.
Alors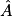
 ° (arrondi au degré).
° (arrondi au degré).
Alors
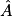
 ° (arrondi au degré).
° (arrondi au degré). b. ABC est un triangle rectangle en B tel que AC = 3 et AB = 2.
Alors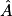
 ° (arrondi au degré).
° (arrondi au degré).
Alors
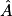
 ° (arrondi au degré).
° (arrondi au degré). c. ABC est un triangle rectangle en B tel que AB = 2 et BC = 3.
Alors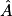
 ° (arrondi au degré).
° (arrondi au degré).
Alors
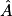
 ° (arrondi au degré).
° (arrondi au degré). a. On connaît AC et BC ; pour calculer, on utilise 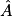 :
:
sin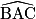 =
= 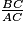 =
= 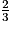
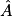 :
:sin
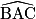 =
= 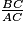 =
= 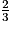
b. On connaît AC et AB ; pour calculer, on utilise 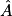 :
:
cos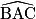 =
= 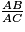 =
= 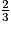
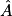 :
:cos
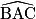 =
= 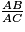 =
= 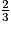
c. On connaît AB et BC ; pour calculer, on utilise 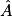 :
:
tan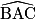 =
= 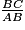 =
= 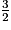
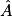 :
:tan
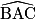 =
= 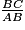 =
=