Signaler une erreur
Mathématiques - Travailler sur des sujets corrigés
Sujet 0, épreuve commune, exercice 2, 2019
Mathématiques - Travailler sur des sujets corrigés
Sujet 0, épreuve commune, exercice 2, 2019
Imprimer
Mathématiques - Travailler sur des sujets corrigés
Sujet 0, épreuve commune, exercice 2, 2019
Mathématiques - Travailler sur des sujets corrigés
Sujet 0, épreuve commune, exercice 2, 2019
Exercice 2 (5 points)
Une entreprise de menuiserie réalise des découpes dans des plaques rectangulaires de bois.
Dans le repère orthonormé d'unité 30 cm ci-dessous, on modélise la forme de la découpe dans la plaque rectangulaire par la courbe Cf représentative de la fonction f définie sur l'intervalle [− 1 ;2] par
f(x) = (−x + 2)ex.
Dans le repère orthonormé d'unité 30 cm ci-dessous, on modélise la forme de la découpe dans la plaque rectangulaire par la courbe Cf représentative de la fonction f définie sur l'intervalle [− 1 ;2] par
f(x) = (−x + 2)ex.
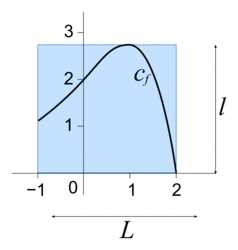 |
Le bord supérieur de la plaque rectangulaire est tangent à la courbe Cf. On nomme L la longueur de la plaque rectangulaire et l sa largeur.
1.
On note f' la fonction dérivée de f.
a. Montrer que pour tout réel x de l'intervalle [−1 ; 2], f'(x) = (−x + 1)ex.
b. En déduire le tableau de variations de la fonction f sur [−1 ; 2].
2. La longueur L de la plaque rectangulaire est 90 cm. Trouver sa largeur l exacte en cm.
Corrigé
Exercice 2 :
La fonction exponentielle est dérivable sur  et sa fonction dérivée est elle-même.
et sa fonction dérivée est elle-même.
Lorsqu'une fonction f est de la forme u× v, avec u et v deux fonctions dérivables sur un intervalle I, alors f est dérivable sur I et :
f' = u' × v + v' × u.
Le sens de variation d'une fonction f est lié au signe de la fonction dérivée f'.
f' est positive sur I si et seulement si f est croissante sur I.
f' est négative sur si I et seulement si f est décroissante sur I.
 et sa fonction dérivée est elle-même.
et sa fonction dérivée est elle-même.Lorsqu'une fonction f est de la forme u× v, avec u et v deux fonctions dérivables sur un intervalle I, alors f est dérivable sur I et :
f' = u' × v + v' × u.
Le sens de variation d'une fonction f est lié au signe de la fonction dérivée f'.
f' est positive sur I si et seulement si f est croissante sur I.
f' est négative sur si I et seulement si f est décroissante sur I.
1.
a. f est dérivable sur [−1 ; 2] en tant que produit d'une fonction affine et de la fonction exponentielle.
Pour tout x de [−1 ; 2],f '(x) = (−1) × ex + ex × (−x + 2)
L'expression est une somme de deux termes ayant un facteur commun, ex. On factorise donc par ex :
f'(x) = ex[(−1) + (−x + 2)]
f'(x) = ex(−x + 1)
Pour tout x de [−1 ; 2],f '(x) = (−1) × ex + ex × (−x + 2)
L'expression est une somme de deux termes ayant un facteur commun, ex. On factorise donc par ex :
f'(x) = ex[(−1) + (−x + 2)]
f'(x) = ex(−x + 1)
b. Pour tout x de [−1 ; 2], ex > 0.
−x + 1 = 0 si et seulement si x = 1. Et −x + 1 est du style −mx + p avec m = −1 < 0 donc :
−x + 1 = 0 si et seulement si x = 1. Et −x + 1 est du style −mx + p avec m = −1 < 0 donc :
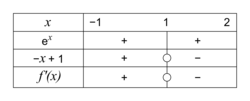 |
Ainsi f strictement croissante sur [−1 ; 1] et strictement décroissante sur [1 ; 2].
De plus :
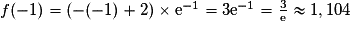
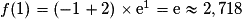
f(2) = (−2 + 2) × e2 = 0.
Voici le tableau de variations de la fonction f :
De plus :
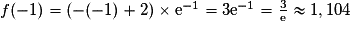
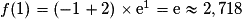
f(2) = (−2 + 2) × e2 = 0.
Voici le tableau de variations de la fonction f :
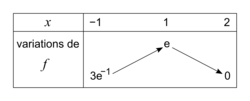 |
2. Une unité représente 30 cm. Or f(1) = e donc la largeur l de la plaque rectangulaire est 30 × e cm (soit environ 81,55 cm).
En effet, comme f est dérivable sur [−1 ; 2] et f' s'annule en changeant de signe en x = 1, alors f admet un maximum atteint lorsque x = 1 et qui vaut f(1), soit e.
En effet, comme f est dérivable sur [−1 ; 2] et f' s'annule en changeant de signe en x = 1, alors f admet un maximum atteint lorsque x = 1 et qui vaut f(1), soit e.
Corrigé
Exercice 2 :
La fonction exponentielle est dérivable sur  et sa fonction dérivée est elle-même.
et sa fonction dérivée est elle-même.
Lorsqu'une fonction f est de la forme u× v, avec u et v deux fonctions dérivables sur un intervalle I, alors f est dérivable sur I et :
f' = u' × v + v' × u.
Le sens de variation d'une fonction f est lié au signe de la fonction dérivée f'.
f' est positive sur I si et seulement si f est croissante sur I.
f' est négative sur si I et seulement si f est décroissante sur I.
 et sa fonction dérivée est elle-même.
et sa fonction dérivée est elle-même.Lorsqu'une fonction f est de la forme u× v, avec u et v deux fonctions dérivables sur un intervalle I, alors f est dérivable sur I et :
f' = u' × v + v' × u.
Le sens de variation d'une fonction f est lié au signe de la fonction dérivée f'.
f' est positive sur I si et seulement si f est croissante sur I.
f' est négative sur si I et seulement si f est décroissante sur I.
1.
a. f est dérivable sur [−1 ; 2] en tant que produit d'une fonction affine et de la fonction exponentielle.
Pour tout x de [−1 ; 2],f '(x) = (−1) × ex + ex × (−x + 2)
L'expression est une somme de deux termes ayant un facteur commun, ex. On factorise donc par ex :
f'(x) = ex[(−1) + (−x + 2)]
f'(x) = ex(−x + 1)
Pour tout x de [−1 ; 2],f '(x) = (−1) × ex + ex × (−x + 2)
L'expression est une somme de deux termes ayant un facteur commun, ex. On factorise donc par ex :
f'(x) = ex[(−1) + (−x + 2)]
f'(x) = ex(−x + 1)
b. Pour tout x de [−1 ; 2], ex > 0.
−x + 1 = 0 si et seulement si x = 1. Et −x + 1 est du style −mx + p avec m = −1 < 0 donc :
−x + 1 = 0 si et seulement si x = 1. Et −x + 1 est du style −mx + p avec m = −1 < 0 donc :
 |
Ainsi f strictement croissante sur [−1 ; 1] et strictement décroissante sur [1 ; 2].
De plus :
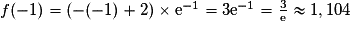
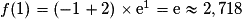
f(2) = (−2 + 2) × e2 = 0.
Voici le tableau de variations de la fonction f :
De plus :
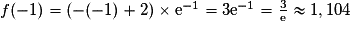
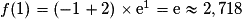
f(2) = (−2 + 2) × e2 = 0.
Voici le tableau de variations de la fonction f :
 |
2. Une unité représente 30 cm. Or f(1) = e donc la largeur l de la plaque rectangulaire est 30 × e cm (soit environ 81,55 cm).
En effet, comme f est dérivable sur [−1 ; 2] et f' s'annule en changeant de signe en x = 1, alors f admet un maximum atteint lorsque x = 1 et qui vaut f(1), soit e.
En effet, comme f est dérivable sur [−1 ; 2] et f' s'annule en changeant de signe en x = 1, alors f admet un maximum atteint lorsque x = 1 et qui vaut f(1), soit e.
Signaler une erreur
Mathématiques - Travailler sur des sujets corrigés
Sujet 0, épreuve commune, exercice 2, 2019
Mathématiques - Travailler sur des sujets corrigés
Sujet 0, épreuve commune, exercice 2, 2019
Imprimer
Mathématiques - Travailler sur des sujets corrigés
Sujet 0, épreuve commune, exercice 2, 2019
Mathématiques - Travailler sur des sujets corrigés
Sujet 0, épreuve commune, exercice 2, 2019

