Sujet zéro, épreuve commune, sujet 3, des instruments, des notes et des gammes, 2020
Énoncé
Les instruments de musique produisent des sons auxquels l'oreille humaine associe certaines caractéristiques : hauteur, timbre et intensité. La répartition des notes dans une gamme a été retenue pour qu'elles sonnent de manière harmonieuse les unes par rapport aux autres. La recherche de cette harmonie a conduit à différents types de gammes, des gammes dites de Pythagore aux gammes tempérées.
Le sujet est composé de deux parties largement indépendantes.
Partie 1 : Des instruments et des notes
Les cordes d'un piano vibrent lorsqu'elles sont frappées par de petits marteaux actionnés par les touches du clavier. Les sons produits par le piano résultent de ces vibrations.
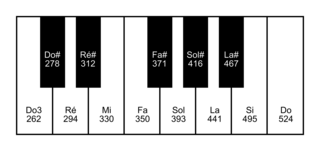 |
1. Calculer la fréquence associée au La4 situé une octave au-dessus du La3.
Lorsqu'on passe d'une octave à la suivante, le rapport de leur fréquence est égal à 2.
2. On s'intéresse aux sons produits par ce piano. Un système d'acquisition informatisé permet l'enregistrement et la visualisation des signaux associés à ces sons.
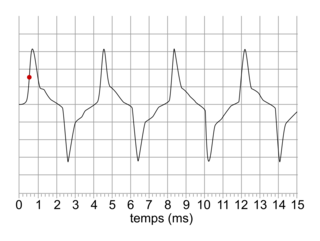
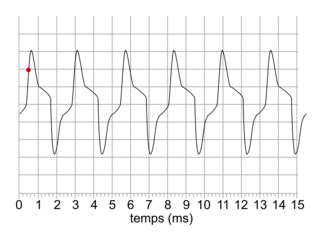
Document 2. Signaux enregistrés correspondant à des notes de musique jouées par un piano.
|
|
2. 1. Justifier que les figures 1 et 2 correspondent à deux notes différentes.
Deux mêmes notes ont la même fréquence.
2. 2. Identifier les notes correspondant aux figures 1 et 2.
Pour identifier les notes, il faut déterminer leur fréquence et donc leur période. Pour une meilleure précision, il vaut mieux mesurer plusieurs périodes.
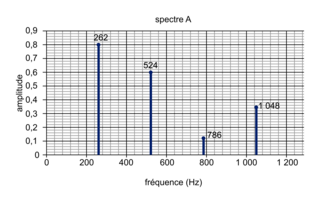
3. L'analyse spectrale permet, après une acquisition informatisée et un traitement numérique, de révéler la « signature acoustique » d'un son en faisant apparaître l'amplitude de ses différentes composantes en fréquence.
 |
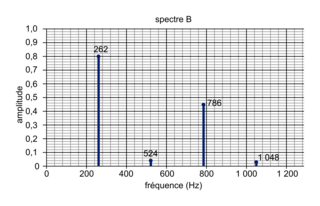 |
Figure 3.
Spectres de sons produits par deux instruments de musique (fréquence de chaque composante indiquée en hertz)
Spectres de sons produits par deux instruments de musique (fréquence de chaque composante indiquée en hertz)
3. 1. Ces deux sons ont-ils la même hauteur ? L'oreille humaine peut-elle les différencier ?
La hauteur d'un son correspond à la fréquence de son fondamental.
3. 2. Le spectre a correspond à l'un des sons produit par un piano étudiés dans la question 2. Associer ce spectre à l'un des deux signaux du document 2.
La fréquence du fondamental d'un son correspond à la fréquence de la note produite. Utiliser les questions précédentes pour associer le spectre au signal du document 2.
Partie 2 : Des notes et des gammes
La théorie musicale étant fondée sur des rapports de fréquences, on décide de simplifier les calculs en attribuant la valeur 1 (sans unité) à une fréquence choisie comme référence. Celle-ci correspond à une note de référence (par exemple 262 Hz pour le Do3). On retrouve ensuite les fréquences réelles en multipliant les valeurs calculées par la fréquence de la note de référence.
La construction des gammes dites de Pythagore est basée sur le cycle des quintes : on part de la fréquence de valeur f0 = 1. On construit une nouvelle fréquence, la quinte, en multipliant f0 par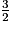 . On réitère ce processus pour obtenir la quinte de la quinte, et ainsi de suite. À certaines étapes, le fait de multiplier par
. On réitère ce processus pour obtenir la quinte de la quinte, et ainsi de suite. À certaines étapes, le fait de multiplier par 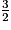 une fréquence comprise entre 1 et 2 peut donner une fréquence supérieure ou égale à 2. On se propose de démontrer que, si on divise par 2 la valeur obtenue, on la ramène dans l'octave.
une fréquence comprise entre 1 et 2 peut donner une fréquence supérieure ou égale à 2. On se propose de démontrer que, si on divise par 2 la valeur obtenue, on la ramène dans l'octave.
La construction des gammes dites de Pythagore est basée sur le cycle des quintes : on part de la fréquence de valeur f0 = 1. On construit une nouvelle fréquence, la quinte, en multipliant f0 par
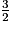 . On réitère ce processus pour obtenir la quinte de la quinte, et ainsi de suite. À certaines étapes, le fait de multiplier par
. On réitère ce processus pour obtenir la quinte de la quinte, et ainsi de suite. À certaines étapes, le fait de multiplier par 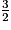 une fréquence comprise entre 1 et 2 peut donner une fréquence supérieure ou égale à 2. On se propose de démontrer que, si on divise par 2 la valeur obtenue, on la ramène dans l'octave.
une fréquence comprise entre 1 et 2 peut donner une fréquence supérieure ou égale à 2. On se propose de démontrer que, si on divise par 2 la valeur obtenue, on la ramène dans l'octave.4.
On suppose que 1 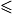 f < 2 et on raisonne par disjonction de cas :
f < 2 et on raisonne par disjonction de cas :
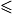 f < 2 et on raisonne par disjonction de cas :
f < 2 et on raisonne par disjonction de cas :• premier cas : 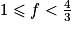 . Montrer que
. Montrer que 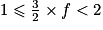 ;
;
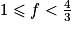 . Montrer que
. Montrer que 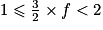 ;
;• deuxième cas : 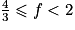 . Montrer que
. Montrer que 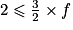 et
et 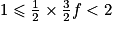 .
.
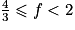 . Montrer que
. Montrer que 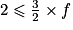 et
et 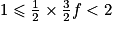 .
.Utiliser chaque inégalité donnée, en transposant des coefficients on obtiendra les inégalités à démontrer.
5. L'algorithme suivant permet de calculer les fréquences des notes successivement obtenues par ce processus jusqu'à ce qu'on retombe sur la fréquence initiale.
f ← 1
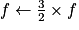
n ← 1
Tant que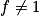 faire
faire
n ← n + 1
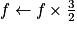
Si f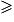 2 alors
2 alors 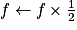
Fin Si
Fin Tant que
Recopier et compléter le tableau ci-dessous en donnant les valeurs des 12 premières quintes obtenues par cet algorithme. Les résultats seront donnés d'abord sous forme exacte comme quotients d'une puissance de 2 par une puissance de 3, puis par leurs valeurs décimales approchées au centième obtenues à l'aide de la calculatrice.
f ← 1
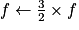
n ← 1
Tant que
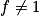 faire
fairen ← n + 1
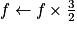
Si f
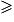 2 alors
2 alors 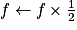
Fin Si
Fin Tant que
Recopier et compléter le tableau ci-dessous en donnant les valeurs des 12 premières quintes obtenues par cet algorithme. Les résultats seront donnés d'abord sous forme exacte comme quotients d'une puissance de 2 par une puissance de 3, puis par leurs valeurs décimales approchées au centième obtenues à l'aide de la calculatrice.
| Numéro de la note | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Fréquence (fraction irréductible) | 1 | 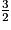 | | | | 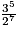 | 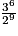 | 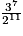 | | 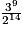 | 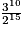 | 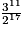 | 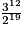 |
| Fréquence (valeur approchée à 10−2 près) | 1 | 1,5 | | | | 1,9 | 1,42 | 1,07 | | 1,20 | 1,80 | 1,35 | 1,01 |
Chaque note suivante a une fréquence dont la valeur est calculée par l'algorithme donné.
6. L'algorithme termine-t-il pour une valeur de n inférieure ou égale à 12 ?
Analyser la condition dans le « tant que » puis la comparer au tableau de valeurs calculées précédemment.
7.
Chacune des fréquences calculées est obtenue à partir de 1 par multiplications successives par 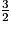 et parfois par
et parfois par 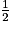 . Elles peuvent donc toutes s'écrire sous la forme
. Elles peuvent donc toutes s'écrire sous la forme 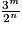 où m et n sont des entiers naturels non nuls.
où m et n sont des entiers naturels non nuls.
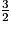 et parfois par
et parfois par 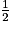 . Elles peuvent donc toutes s'écrire sous la forme
. Elles peuvent donc toutes s'écrire sous la forme 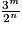 où m et n sont des entiers naturels non nuls.
où m et n sont des entiers naturels non nuls.7. 1. Démontrer que l'égalité 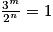 est impossible.
est impossible.
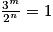 est impossible.
est impossible.Pour résoudre l'équation, faire un produit en croix et procéder par un raisonnement par l'absurde.
7. 2. Que peut-on en déduire pour l'algorithme proposé ci-dessus ?
Analyser de nouveau la condition de la boucle « tant que » avec la réponse à la question précédente.
8. D'après ce qui précède, le cycle des quintes ne « reboucle » jamais exactement sur la note de départ. En s'appuyant sur le tableau de la question 4, justifier le choix de 12 notes dans une gamme construite selon ce principe.
Analyser la valeur de la fréquence pour la douzième note.
Corrigé
1. La fréquence associée au La4 qui est à l'octave au-dessus du La3 a donc une valeur deux fois plus grande. Soit, en Hz : f = 2 × 441 = 882.
2. 1. Comme la période est l'inverse de la fréquence et que les périodes des deux signaux sont différentes, alors les deux notes jouées sont différentes.
2. 2. Sur le signal de la figure 1, on peut mesurer 3 périodes :
3T= 11,5 div. Or 1 div représente 1 ms donc 3T = 11,5 ms = 11,5 × 10−3 s,
soit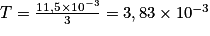 (en s).
(en s).
Comme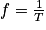 , on obtient
, on obtient 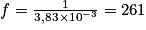 (en Hz). Il s'agit du Do3.
(en Hz). Il s'agit du Do3.
De même, pour le signal de la figure 2, on mesure 4 périodes :
4T = 10,2 div. Or 1 div représente 1 ms donc 4T = 10,2 × 10−3 s,
soit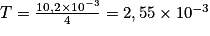 (en s).
(en s).
Comme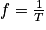 , on obtient
, on obtient 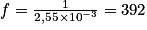 (en Hz). Il s'agit du Sol3.
(en Hz). Il s'agit du Sol3.
3T= 11,5 div. Or 1 div représente 1 ms donc 3T = 11,5 ms = 11,5 × 10−3 s,
soit
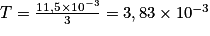 (en s).
(en s).Comme
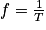 , on obtient
, on obtient 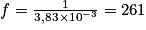 (en Hz). Il s'agit du Do3.
(en Hz). Il s'agit du Do3.De même, pour le signal de la figure 2, on mesure 4 périodes :
4T = 10,2 div. Or 1 div représente 1 ms donc 4T = 10,2 × 10−3 s,
soit
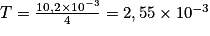 (en s).
(en s).Comme
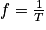 , on obtient
, on obtient 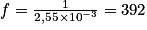 (en Hz). Il s'agit du Sol3.
(en Hz). Il s'agit du Sol3.3. 1. La fréquence du fondamental pour le spectre a et pour le spectre b vaut 262 Hz. La hauteur étant la même. La répartition des autres harmoniques diffère d'un spectre à l'autre : le timbre est différent. L'oreille humaine pourra donc les différencier par rapport à leur timbre.
3. 2. La fréquence du fondamental est de 262 Hz : elle correspond au Do3. D'après la question précédente, le signal correspondant au Do3 est le signal de la figure 1 sur le document 2.
4. Dans le premier cas, on a 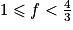 .
.
On multiplie tous les membres par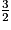 , on obtient :
, on obtient : 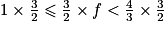 ,
,
soit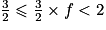 , et comme
, et comme 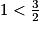 , on obtient
, on obtient 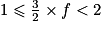 .
.
Dans le deuxième cas, on a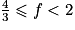 .
.
On multiplie tous les membres par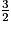 , on obtient :
, on obtient : 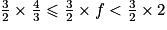 ,
,
soit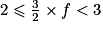 . En multipliant tous les membres par
. En multipliant tous les membres par 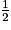 :
: 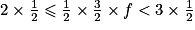 ,
,
on obtient :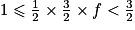 et
et 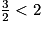 donc :
donc : 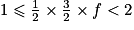 .
.
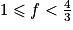 .
.On multiplie tous les membres par
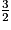 , on obtient :
, on obtient : 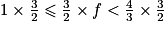 ,
,soit
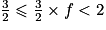 , et comme
, et comme 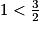 , on obtient
, on obtient 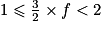 .
.Dans le deuxième cas, on a
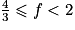 .
.On multiplie tous les membres par
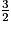 , on obtient :
, on obtient : 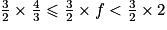 ,
,soit
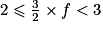 . En multipliant tous les membres par
. En multipliant tous les membres par 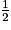 :
: 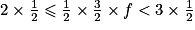 ,
,on obtient :
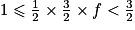 et
et 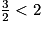 donc :
donc : 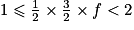 .
.5. L'algorithme multiplie la fréquence par 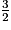 .
.
Si la fréquence devient supérieure à 2 alors la fréquence est multipliée par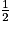 .
.
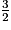 .
.Si la fréquence devient supérieure à 2 alors la fréquence est multipliée par
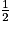 .
.| Numéro de la note | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Fréquence (fraction irréductible) | 1 | 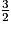 | 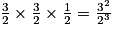 | 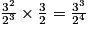 | 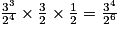 | 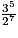 | 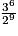 | 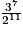 | 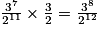 | 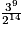 | 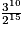 | 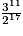 | 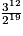 |
| Fréquence (valeur approchée à 10−2 près) | 1 | 1,5 | 1,13 | 1,69 | 1,27 | 1,9 | 1,42 | 1,07 | 1,60 | 1,20 | 1,80 | 1,35 | 1,01 |
6. La boucle « tant que » de l'algorithme termine si la condition f = 1 est remplie. Or, d'après le tableau précédent, la fréquence n'est jamais égale à 1. Donc l'algorithme ne termine pas pour les notes numérotées de 0 à 12.
7. 1. Résoudre 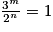 revient à résoudre 3m = 2n. Or toutes les puissances de 3 sont des entiers impairs et toutes les puissances de 2 sont des entiers pairs, pour n non nul. Il est donc impossible de trouver deux entiers m et n qui satisfassent l'équation : l'équation proposée est impossible.
revient à résoudre 3m = 2n. Or toutes les puissances de 3 sont des entiers impairs et toutes les puissances de 2 sont des entiers pairs, pour n non nul. Il est donc impossible de trouver deux entiers m et n qui satisfassent l'équation : l'équation proposée est impossible.
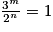 revient à résoudre 3m = 2n. Or toutes les puissances de 3 sont des entiers impairs et toutes les puissances de 2 sont des entiers pairs, pour n non nul. Il est donc impossible de trouver deux entiers m et n qui satisfassent l'équation : l'équation proposée est impossible.
revient à résoudre 3m = 2n. Or toutes les puissances de 3 sont des entiers impairs et toutes les puissances de 2 sont des entiers pairs, pour n non nul. Il est donc impossible de trouver deux entiers m et n qui satisfassent l'équation : l'équation proposée est impossible.7. 2. Comme l'algorithme proposé multiplie la fréquence par 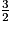 et/ou par
et/ou par 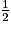 , donc par
, donc par 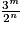 , et que le rapport
, et que le rapport 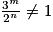 , on peut conclure que l'algorithme ne s'arrête pas puisque la condition d'arrêt n'est jamais atteinte.
, on peut conclure que l'algorithme ne s'arrête pas puisque la condition d'arrêt n'est jamais atteinte.
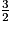 et/ou par
et/ou par 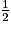 , donc par
, donc par 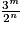 , et que le rapport
, et que le rapport 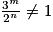 , on peut conclure que l'algorithme ne s'arrête pas puisque la condition d'arrêt n'est jamais atteinte.
, on peut conclure que l'algorithme ne s'arrête pas puisque la condition d'arrêt n'est jamais atteinte.8. Le cycle des quintes ne reboucle jamais exactement sur la note de départ, car 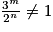 . En revanche, on peut observer que la fréquence de la note numéro 12 est égale à 1,01 qui est proche de 1. On peut ainsi considérer que la note numéro 12 a une fréquence qui revient quasiment à la fréquence de départ. Les notes du numéro 0 au numéro 12 forment ainsi une suite finie répartie dans une octave.
. En revanche, on peut observer que la fréquence de la note numéro 12 est égale à 1,01 qui est proche de 1. On peut ainsi considérer que la note numéro 12 a une fréquence qui revient quasiment à la fréquence de départ. Les notes du numéro 0 au numéro 12 forment ainsi une suite finie répartie dans une octave.
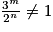 . En revanche, on peut observer que la fréquence de la note numéro 12 est égale à 1,01 qui est proche de 1. On peut ainsi considérer que la note numéro 12 a une fréquence qui revient quasiment à la fréquence de départ. Les notes du numéro 0 au numéro 12 forment ainsi une suite finie répartie dans une octave.
. En revanche, on peut observer que la fréquence de la note numéro 12 est égale à 1,01 qui est proche de 1. On peut ainsi considérer que la note numéro 12 a une fréquence qui revient quasiment à la fréquence de départ. Les notes du numéro 0 au numéro 12 forment ainsi une suite finie répartie dans une octave.