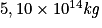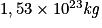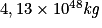Au xixe siècle, les scientifiques se demandaient comment le soleil brillait et quelles étaient les sources des énormes quantités d'énergie nécessaires à la vie sur Terre. Ce n'est qu'au milieu du xxe siècle, avec la découverte des réactions de fission et de fusion nucléaire, qu'on a pu répondre précisément à ces questions.
I. Quelles sont les réactions de fusion qui se produisent dans les étoiles ?
• Une étoile naît de la contraction d'un nuage composé essentiellement d'hydrogène. Sous l'effet de la contraction, le cœur de l'étoile atteint des valeurs de pression et de température extrêmes. En effet, l'étoile convertit son énergie gravitationnelle en énergie thermique. La température au centre du Soleil peut atteindre 15 millions de degrés. Les noyaux sont dissociés de leurs électrons : la matière est un gaz ionisé. On parle d'état plasma. Ainsi les noyaux libres donnent lieu lors de chocs entre eux à des réactions de fusion nucléaire en libérant de l'énergie.
• La très grande température qui règne dans les étoiles permet de surmonter la répulsion électrostatique entre deux noyaux d'hydrogène. Ainsi, dans une première étape, deux protons 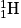 (noyaux d'hydrogène dépossédés de leur électron) interagissent pour former un noyau de deutérium
(noyaux d'hydrogène dépossédés de leur électron) interagissent pour former un noyau de deutérium 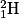 . On note qu'un proton s'est transformé en neutron et qu'il y a libération d'un positron
. On note qu'un proton s'est transformé en neutron et qu'il y a libération d'un positron 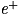 (particule identique à un électron, mais de charge contraire) et d'un neutrino ν (particule neutre de masse très faible) :
(particule identique à un électron, mais de charge contraire) et d'un neutrino ν (particule neutre de masse très faible) :
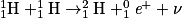
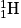 (noyaux d'hydrogène dépossédés de leur électron) interagissent pour former un noyau de deutérium
(noyaux d'hydrogène dépossédés de leur électron) interagissent pour former un noyau de deutérium 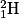 . On note qu'un proton s'est transformé en neutron et qu'il y a libération d'un positron
. On note qu'un proton s'est transformé en neutron et qu'il y a libération d'un positron 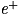 (particule identique à un électron, mais de charge contraire) et d'un neutrino ν (particule neutre de masse très faible) :
(particule identique à un électron, mais de charge contraire) et d'un neutrino ν (particule neutre de masse très faible) :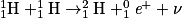
• Dans une deuxième étape, le noyau de deutérium fusionne avec un proton pour former un noyau d'hélium 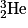 et un photon γ (correspondant à une radiation) :
et un photon γ (correspondant à une radiation) :
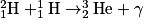
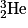 et un photon γ (correspondant à une radiation) :
et un photon γ (correspondant à une radiation) :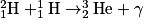
• Dans une troisième étape, deux noyaux d'hélium 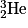 fusionnent pour former un noyau d'hélium
fusionnent pour former un noyau d'hélium 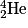 et deux protons :
et deux protons :
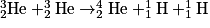
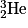 fusionnent pour former un noyau d'hélium
fusionnent pour former un noyau d'hélium 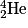 et deux protons :
et deux protons :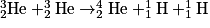
• Le bilan de ce cycle appelé cycle proton-proton est : 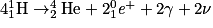
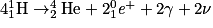
• Ces réactions produisent une énorme quantité d'énergie qui donne naissance à une pression au cœur qui va s'opposer à la force de gravitation et arrête la contraction de l'étoile. C'est la fin de la naissance de l'étoile. Elle va ensuite vivre sur ses réserves.
• Lorsque la concentration en hélium atteint une valeur seuil, la pression au cœur diminue et l'étoile se contracte : la température et la pression augmentent de nouveau. De nouvelles réactions de fusion sont alors possibles pour obtenir des noyaux plus lourds comme le béryllium : 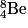 , le carbone
, le carbone 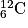 , le néon
, le néon 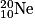 , l'oxygène
, l'oxygène 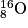 ou le silicium
ou le silicium 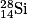 .
.
Exercice n°1
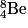 , le carbone
, le carbone 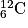 , le néon
, le néon 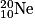 , l'oxygène
, l'oxygène 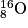 ou le silicium
ou le silicium 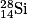 .
.Exercice n°1
II. Quelle quantité d'énergie est fournie par le Soleil ?
• Le Soleil rayonne une grande quantité d'énergie. Or l'affirmation de Lavoisier « Rien ne se perd, rien ne se crée, tout se transforme » s'applique aussi ici. Lors de la réaction bilan précédente, la masse du noyau d'hélium produit est légèrement inférieure à la somme des masses des quatre protons. On dit que la réaction nucléaire s'accompagne d'une perte de masse. Or Einstein montra avec sa célèbre formule, 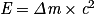 , que l'énergie est proportionnelle à la perte de masse. c est la vitesse de la lumière dans le vide.
, que l'énergie est proportionnelle à la perte de masse. c est la vitesse de la lumière dans le vide.
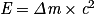 , que l'énergie est proportionnelle à la perte de masse. c est la vitesse de la lumière dans le vide.
, que l'énergie est proportionnelle à la perte de masse. c est la vitesse de la lumière dans le vide.• La luminosité solaire nominale vaut 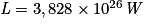 . On calcule que l'énergie solaire fournie en une seconde est donc :
. On calcule que l'énergie solaire fournie en une seconde est donc :
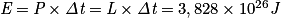
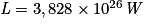 . On calcule que l'énergie solaire fournie en une seconde est donc :
. On calcule que l'énergie solaire fournie en une seconde est donc :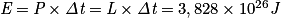
• Avec la relation d'Einstein, on peut déterminer la perte de masse par seconde dans le Soleil :
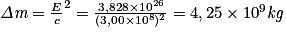
soit une perte de masse de plus de 4 millions de tonnes par seconde.
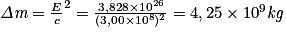
soit une perte de masse de plus de 4 millions de tonnes par seconde.
• Dans le Soleil, la perte de masse correspond à une libération d'énergie considérable. Le Soleil transforme sa masse en énergie qui va le faire briller pendant encore 5 milliards d'années environ. Cette énergie correspond au rayonnement électromagnétique.
Exercice n°2
Exercice n°2
III. Comment détermine-t-on la longueur d'onde du rayonnement émis par une étoile ?
• On dit que le Soleil, comme toutes les étoiles, peut être classé dans la catégorie des corps noirs. Un corps noir est un corps idéal qui absorbe toute l'énergie électromagnétique qu'il reçoit : il ne la réfléchit pas ni ne la transmet.
• On remarque qu'un tel corps est un modèle irréaliste puisque sa température augmenterait indéfiniment. Un corps noir réémet donc une partie de l'énergie qu'il absorbe, sous forme de rayonnement électromagnétique.
• De plus, ce rayonnement possède un spectre de couleurs qui nous permet de déterminer la température de l'étoile. Si on chauffe le filament d'une lampe progressivement à une température T1, puis T2 et enfin T3 avec T1 < T2 < T3. On analyse la lumière et on obtient les spectres continus suivants :
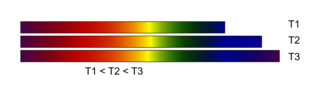 |
• Les spectres nous montrent que pour les températures faibles, le corps chaud est rouge. Si la température augmente, le vert se superpose au rouge pour donner du jaune, comme le Soleil. Si la température augmente encore, le spectre contient du bleu, on voit l'objet blanc.
• Un corps chaud émet un spectre d'émission continu dont la composition dépend de la température. La loi de Wien permet de déterminer la température de surface d'une étoile. Elle exprime le fait que la longueur d'onde maximale émise par le corps noir est inversement proportionnelle à sa température de surface :
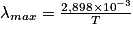
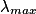 est la longueur d'onde maximale en mètre. T est la température de surface en Kelvin.
est la longueur d'onde maximale en mètre. T est la température de surface en Kelvin.
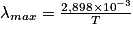
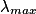 est la longueur d'onde maximale en mètre. T est la température de surface en Kelvin.
est la longueur d'onde maximale en mètre. T est la température de surface en Kelvin.• Si on appelle 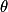 la température en degré Celsius, alors on a la conversion suivante :
la température en degré Celsius, alors on a la conversion suivante :
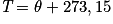
Plus la température est chaude et plus la longueur d'onde maximale est petite. On dit que la lumière émise par la source s'enrichit de petites longueurs d'onde.
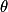 la température en degré Celsius, alors on a la conversion suivante :
la température en degré Celsius, alors on a la conversion suivante : 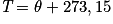
Plus la température est chaude et plus la longueur d'onde maximale est petite. On dit que la lumière émise par la source s'enrichit de petites longueurs d'onde.
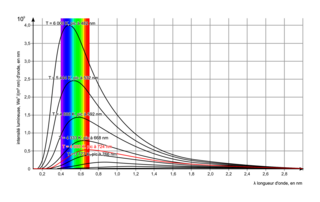 |
• On voit que pour une température de 6 000 K, la longueur d'onde maximale d'émission est :
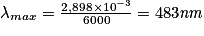
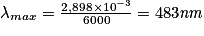
• Pour une température de 4 000 K, la longueur d'onde maximale d'émission est :
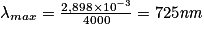
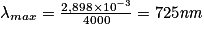
• Ainsi, un corps noir à 9 000 K apparaîtra bleuté alors qu'un corps noir à 5 000 K apparaîtra orangé, car la longueur d'onde maximale émise sera plus grande.
Exercice n°3
Exercice n°3
IV. Quelle est la température de surface de l'étoile ?
• D'après la relation précédente, les étoiles les plus « froides » sont rouges. Leur température de surface est de l'ordre de 2 000 K. Les étoiles blanches, comme Sirius, ont des températures de l'ordre de 11 000 K alors que les étoiles bleues comme Rigel peuvent atteindre 20 000 K. Ces dernières émettent surtout dans les ultra-violets. Par conséquent, une étoile apparaissant rouge dans le ciel sera plus froide qu'une étoile apparaissant bleue.
• Attention toutefois, la couleur apparente d'une étoile ne va pas exactement correspondre à la température de sa longueur d'onde maximale émise donnée par la loi de Wien. En effet, la couleur perçue va intégrer également de l'énergie rayonnée. Ainsi, on peut donner la température de surface d'une étoile qui nous renseigne sur la couleur.
• Vérifions la température de surface du Soleil. D'après le spectre ci-dessous, la longueur d'onde maximale d'émission est environ égale à 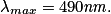
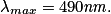
• Avec la loi de Wien, on en déduit : 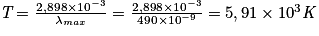
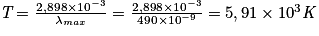
• Compte tenu de la conversion, on trouve : 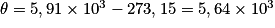 °C
°C
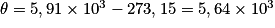 °C
°C• Les tables donnent une température de surface pour le Soleil de 5 578 K, soit 5 305 °C. Les valeurs sont donc en accord.
• La courbe de rayonnement solaire extraterrestre (non influencé par l'atmosphère) est proche de celle du corps noir à une température de 5 900 K.
Exercice n°4
Exercice n°4
À retenir
La très grande température qui règne dans les étoiles implique que des réactions de fusion de l'hydrogène peuvent avoir lieu.Les réactions de fusion de l'hydrogène dégagent énormément d'énergie, ce qui contribue à maintenir les étoiles à une température élevée.
La puissance, appelée luminosité, rayonnée par le Soleil permet de déterminer l'énergie solaire émise.
La relation d'Einstein
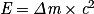 , permet de déterminer la masse perdue par le Soleil. On trouve que le Soleil perd plus de 4 millions de tonnes par seconde.
, permet de déterminer la masse perdue par le Soleil. On trouve que le Soleil perd plus de 4 millions de tonnes par seconde.Plus la température d'un corps est grande et plus sa couleur s'enrichit de bleu : il nous apparaît blanc.
La loi de Wien permet de calculer la température d'un corps en connaissant sa longueur d'onde maximale d'émission ou inversement.
Les étoiles les plus chaudes nous apparaissent bleues tandis que les étoiles les plus « froides » nous apparaissent rouges.
La température de surface du Soleil est environ 5 300°C.
Exercice n°1
Les réactions qui permettent de passer des noyaux d'hydrogène à d'autres types de noyaux plus lourds sont :
Cochez la bonne réponse.
| ||
| ||
|
Dans l'étoile, les noyaux d'hydrogène vont donner des noyaux plus lourds d'hélium. Ce sont donc des réactions de fusion.
Exercice n°2
La luminosité de l'étoile Rigel étant de 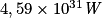 , quelle est la valeur de la perte de masse par seconde dans l'étoile Rigel ?
, quelle est la valeur de la perte de masse par seconde dans l'étoile Rigel ?
Donnée :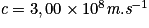
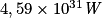 , quelle est la valeur de la perte de masse par seconde dans l'étoile Rigel ?
, quelle est la valeur de la perte de masse par seconde dans l'étoile Rigel ?Donnée :
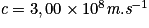
Cochez la bonne réponse.
| ||
| ||
|
Le calcul à réaliser est 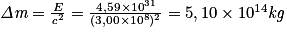 soit 510 milliards de tonnes.
soit 510 milliards de tonnes.
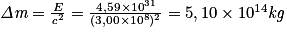 soit 510 milliards de tonnes.
soit 510 milliards de tonnes.Exercice n°3
L'étoile Bételgeuse est une étoile qui a une température de surface de 3 100 °C. Quelle est sa longueur d'onde ?
Donnée :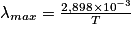 et
et 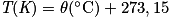
Donnée :
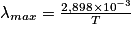 et
et 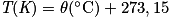
Cochez la bonne réponse.
| ||
| ||
|
Il faut dans un premier temps convertir la température en Kelvin. Soit 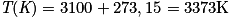
La loi de Wien donne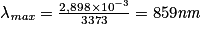
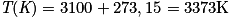
La loi de Wien donne
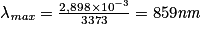
Exercice n°4
Quelle est la température de surface de cette étoile ?
Donnée :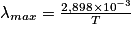 et
et 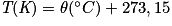
Donnée :
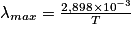 et
et 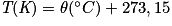
Intensité lumineuse et longueur d'onde
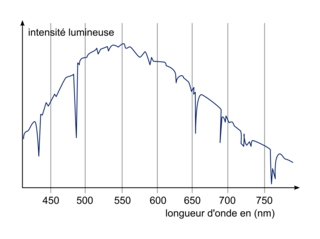 |
Cochez la bonne réponse.
| ||
| ||
|
Il faut déterminer la longueur d'onde maximale d'émission avec la courbe précédente :
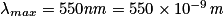
Avec la loi de Wien, on calcule :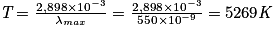
Avec la conversion donnée, on trouve :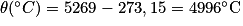 . Soit environ 5 000 °C.
. Soit environ 5 000 °C.
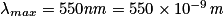
Avec la loi de Wien, on calcule :
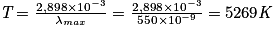
Avec la conversion donnée, on trouve :
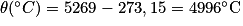 . Soit environ 5 000 °C.
. Soit environ 5 000 °C.