I. Qu'est-ce qu'une fonction dérivée ?
• Définition : Soit une fonction numérique f définie sur un intervalle I et tel que pour tout réel x de I le nombre dérivé de f en x existe.
On dit que la fonction f est dérivable sur I et on appelle fonction dérivée de f la fonction notée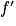 qui est définie sur I et qui à tout réel x lui associe
qui est définie sur I et qui à tout réel x lui associe 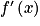 .
.
On dit que la fonction f est dérivable sur I et on appelle fonction dérivée de f la fonction notée
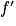 qui est définie sur I et qui à tout réel x lui associe
qui est définie sur I et qui à tout réel x lui associe 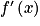 .
.II. Quelles sont les fonctions dérivées à connaître ?
• Les fonctions constantes, la fonction identité, la fonction carré et la fonction cube sont des fonctions définies sur 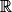 et dérivables sur
et dérivables sur 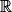 .
.
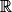 et dérivables sur
et dérivables sur 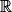 .
. | Fonction | Fonction dérivée |
|---|---|
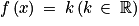 | 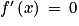 |
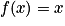 | 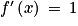 |
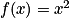 | 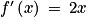 |
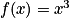 | 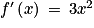 |
• Exemple : Déterminons le nombre dérivé de la fonction cube en −1.
Si pour tout x de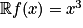 , alors pour tout x de
, alors pour tout x de 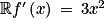 .
.
En particulier on a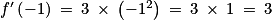 .
.
Ainsi le nombre dérivé de la fonction cube en −1 est 3.
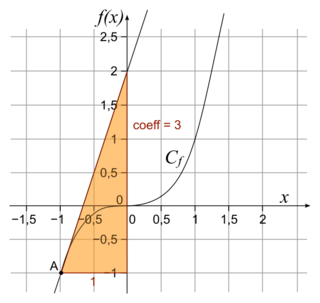
Cela signifie que la courbe représentative de la fonction cube admet une tangente au point A d'abscisse −1 et que cette tangente possède un coefficient directeur égal à 3.
Si pour tout x de
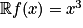 , alors pour tout x de
, alors pour tout x de 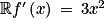 .
.En particulier on a
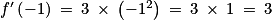 .
.Ainsi le nombre dérivé de la fonction cube en −1 est 3.
Cela signifie que la courbe représentative de la fonction cube admet une tangente au point A d'abscisse −1 et que cette tangente possède un coefficient directeur égal à 3.
• On peut le vérifier à l'aide d'un logiciel de calcul formel en traçant la tangente et en contrôlant la valeur de son coefficient directeur.
 |
III. Comment déterminer l'expression de la fonction dérivée d'une fonction polynomiale de degré 3 ?
• Propriété 1 : Si u et v sont deux fonctions dérivables sur I, alors la fonction (u + v) est dérivable sur I et pour tout x de  .
.
 .
.• Exemple 1 : On considère la fonction f définie sur 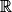 par f(x) = x + 2023.
par f(x) = x + 2023.
En posant u(x) = x et v(x) = 2023, on peut affirmer que :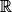 et pour tout x de
et pour tout x de 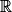 :
: 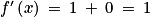 .
.
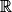 par f(x) = x + 2023.
par f(x) = x + 2023.En posant u(x) = x et v(x) = 2023, on peut affirmer que :
- u est la fonction identité et donc dérivable sur
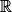 et pour tout x de
et pour tout x de 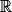 :
: 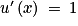 ;
; - v est une fonction constante et donc dérivable sur
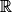 et pour tout x de
et pour tout x de 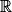 :
: 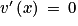 .
.
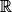 et pour tout x de
et pour tout x de 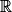 :
: 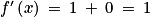 .
.• Propriété 2 : Soit k un réel. Si u est une fonction dérivable sur I, alors la fonction k × u est dérivable sur I et pour tout x de 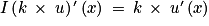 .
.
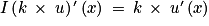 .
.• Exemple 2 : On considère la fonction g définie sur 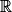 par g(x) = 1 492x3.
par g(x) = 1 492x3.
En posant k = 1 492 et u(x) = x3 on peut affirmer que :
u est la fonction cube et donc dérivable sur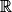 et pour tout x de
et pour tout x de 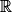 :
: 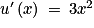 .
.
Ainsi la fonction g est dérivable sur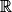 et pour tout x de
et pour tout x de 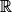 :
: 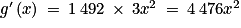 .
.
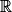 par g(x) = 1 492x3.
par g(x) = 1 492x3.En posant k = 1 492 et u(x) = x3 on peut affirmer que :
u est la fonction cube et donc dérivable sur
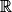 et pour tout x de
et pour tout x de 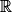 :
: 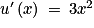 .
.Ainsi la fonction g est dérivable sur
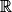 et pour tout x de
et pour tout x de 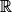 :
: 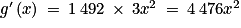 .
.• Exemple 3 : On considère la fonction h définie sur 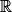 par h(x) = 5x2 + 7x + 3.
par h(x) = 5x2 + 7x + 3.
Déterminons l'expression de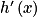 .
.
Pour tout x de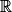 :
:  :
:
 par h(x) = 5x2 + 7x + 3.
par h(x) = 5x2 + 7x + 3.Déterminons l'expression de
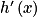 .
.Pour tout x de
 :
: - h(x) = 5 × x2 + 7 × x + 3
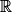 :
: • Remarque : Les fonctions polynomiales sont dérivables sur 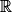 .
.
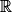 .
.IV. Comment utiliser la dérivation pour étudier les variations d'une fonction ?
• Propriété fondamentale : Soit f une fonction définie et dérivable sur I.
- Si
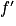 est positive sur I, alors f est croissante sur I.
est positive sur I, alors f est croissante sur I. - Si
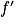 est négative sur I, alors f est décroissante sur I.
est négative sur I, alors f est décroissante sur I.
• Exemple : Soit la fonction g définie pour tout x de 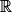 par g(x) = 8x3 + 13x − 17.
par g(x) = 8x3 + 13x − 17.
On cherche à étudier les variations de g sur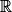 (c'est-à-dire déterminer si g est croissante, décroissante, sur quel(s) intervalle(s), l'existence d'un ou plusieurs extremums…).
(c'est-à-dire déterminer si g est croissante, décroissante, sur quel(s) intervalle(s), l'existence d'un ou plusieurs extremums…).
g est une fonction polynomiale de degré 3, donc g est dérivable sur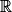 .
.
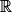 par g(x) = 8x3 + 13x − 17.
par g(x) = 8x3 + 13x − 17.On cherche à étudier les variations de g sur
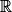 (c'est-à-dire déterminer si g est croissante, décroissante, sur quel(s) intervalle(s), l'existence d'un ou plusieurs extremums…).
(c'est-à-dire déterminer si g est croissante, décroissante, sur quel(s) intervalle(s), l'existence d'un ou plusieurs extremums…).g est une fonction polynomiale de degré 3, donc g est dérivable sur
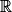 .
.• Pour tout x de 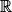 :
: 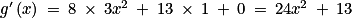 .
.
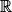 :
: 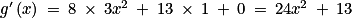 .
.• Or pour tout x de 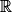 : x2
: x2 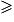 0 (le carré d'un réel est positif ou nul).
0 (le carré d'un réel est positif ou nul).
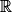 : x2
: x2 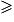 0 (le carré d'un réel est positif ou nul).
0 (le carré d'un réel est positif ou nul).• Donc pour tout x de 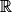 : 24 × x2
: 24 × x2 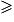 24 × 0 donc 24x2
24 × 0 donc 24x2 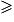 0.
0.
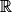 : 24 × x2
: 24 × x2 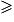 24 × 0 donc 24x2
24 × 0 donc 24x2 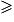 0.
0.• Ainsi pour tout x de 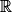 : 24x2 + 13
: 24x2 + 13 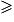 0 + 13. Et on sait que 13 > 0.
0 + 13. Et on sait que 13 > 0.
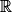 : 24x2 + 13
: 24x2 + 13 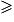 0 + 13. Et on sait que 13 > 0.
0 + 13. Et on sait que 13 > 0.• On a donc prouvé que pour tout x de 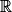 :
: 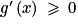 .
.
On peut donc affirmer que la fonction g est croissante sur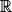 .Exercice n°3
.Exercice n°3
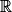 :
: 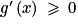 .
.On peut donc affirmer que la fonction g est croissante sur
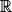 .Exercice n°3
.Exercice n°3V. Comment utiliser la dérivation dans des problèmes d'optimisation ?
• Définition : Soit f définie sur I. Soit c un réel de I.
- Si pour tout x de I f(c)
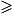 f(x), alors on dit que f admet un maximum égal à f(c) qui est atteint lorsque x = c.
f(x), alors on dit que f admet un maximum égal à f(c) qui est atteint lorsque x = c. - Si pour tout x de I f(c)
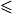 f(x), alors on dit que f admet un minimum égal à f(c) qui est atteint lorsque x = c.
f(x), alors on dit que f admet un minimum égal à f(c) qui est atteint lorsque x = c.
• Propriété : Soit f définie et dérivable sur I. Soit c un réel de I.
- Si
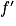 s'annule et change de signe lorsque x = c, alors f admet un extremum local égal à f(c) atteint lorsque x = c.
s'annule et change de signe lorsque x = c, alors f admet un extremum local égal à f(c) atteint lorsque x = c.
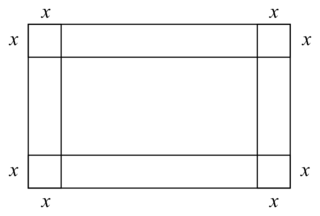
• Exemple : Une entreprise dispose dans sa réserve d'une très grande quantité de feuilles cartonnées rectangulaires de dimension 80 × 50 cm. Elle souhaite fabriquer une boîte de stockage (ayant la forme d'un pavé droit, mais ouvert sur le dessus) qui possède le volume le plus grand possible pour pouvoir y stocker par la suite des sachets de thé.
Pour cela on va découper dans chaque coin de la feuille un carré identique dont la longueur notée x ne pourra excéder 25 cm.
Pour cela on va découper dans chaque coin de la feuille un carré identique dont la longueur notée x ne pourra excéder 25 cm.
 |
• Le réel x appartient à l'intervalle [0 ; 25].
• La base du pavé droit sera donc un rectangle de longueur l = 80 −2 × x et de largeur L = 50 − 2 × x.
• Soit V la fonction qui à x associe le volume du pavé droit en cm3.
• Pour tout x de [0 ; 25] : V(x) = l × L × h = (80 − 2x) × (50 − 2x) × x
V(x) = (80 × 50 − 80 × 2x − 2x × 50 + 2x × 2x) × x
V(x) = (4 000 − 160x − 100x + 4x2) × x
V(x) = 4 000x − 260x2 + 4x3 est une fonction polynomiale de degré 3 donc dérivable sur [0 ; 25].
V(x) = (80 × 50 − 80 × 2x − 2x × 50 + 2x × 2x) × x
V(x) = (4 000 − 160x − 100x + 4x2) × x
V(x) = 4 000x − 260x2 + 4x3 est une fonction polynomiale de degré 3 donc dérivable sur [0 ; 25].
• Pour tout x de [0 ; 25] : 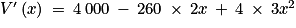
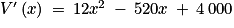
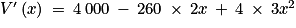
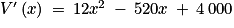
• En utilisant un logiciel de calcul formel, on a :
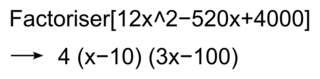 |
• Donc 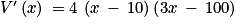 .
.
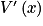 étant un produit, on doit utiliser un tableau de signes pour pouvoir étudier le signe de
étant un produit, on doit utiliser un tableau de signes pour pouvoir étudier le signe de 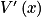 .
.
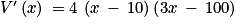 .
.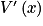 étant un produit, on doit utiliser un tableau de signes pour pouvoir étudier le signe de
étant un produit, on doit utiliser un tableau de signes pour pouvoir étudier le signe de 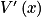 .
.• Le premier facteur 4 ne dépend pas de la variable x et c'est un réel strictement positif.
• Le deuxième facteur x − 10 est nul lorsque x = 10 (en effet 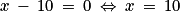 ) et il est positif lorsque x
) et il est positif lorsque x 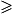 10 (en effet
10 (en effet 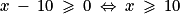 ).
).
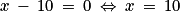 ) et il est positif lorsque x
) et il est positif lorsque x 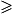 10 (en effet
10 (en effet 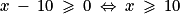 ).
).• Enfin le troisième facteur 3x − 100 est nul lorsque 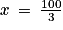 (en effet
(en effet 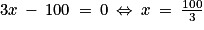 ) et il est positif lorsque
) et il est positif lorsque 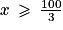 (en effet
(en effet 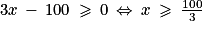 ).
).
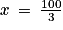 (en effet
(en effet 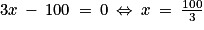 ) et il est positif lorsque
) et il est positif lorsque 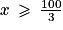 (en effet
(en effet 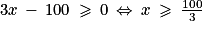 ).
).• ![10\: \in \: \left [ 0\: ;\: 25 \right ]](https://static1.assistancescolaire.com/1/images/1_sci_40_m70.png) mais
mais ![\frac{100}{3}\: \notin \: \left [ 0\: ;\: 25 \right ]](https://static1.assistancescolaire.com/1/images/1_sci_40_m71.png) . On a donc le tableau de signes suivant :
. On a donc le tableau de signes suivant :
![10\: \in \: \left [ 0\: ;\: 25 \right ]](https://static1.assistancescolaire.com/1/images/1_sci_40_m70.png) mais
mais ![\frac{100}{3}\: \notin \: \left [ 0\: ;\: 25 \right ]](https://static1.assistancescolaire.com/1/images/1_sci_40_m71.png) . On a donc le tableau de signes suivant :
. On a donc le tableau de signes suivant : | x | 0 | | 10 | | 25 |
| 4 | | + | | | + | |
| x − 10 | | − | 0 | + | |
| 3x − 100 | | − | | | − | |
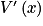 | | + | 0 | − | |
• On peut lire que 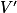 est positive sur [0 ; 10], ce qui signifie que V est croissante sur [0 ; 10].
est positive sur [0 ; 10], ce qui signifie que V est croissante sur [0 ; 10].
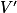 est positive sur [0 ; 10], ce qui signifie que V est croissante sur [0 ; 10].
est positive sur [0 ; 10], ce qui signifie que V est croissante sur [0 ; 10].• De plus 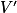 est positive sur [10 ; 25], ce qui signifie que V est croissante sur [10 ; 25].
est positive sur [10 ; 25], ce qui signifie que V est croissante sur [10 ; 25].
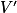 est positive sur [10 ; 25], ce qui signifie que V est croissante sur [10 ; 25].
est positive sur [10 ; 25], ce qui signifie que V est croissante sur [10 ; 25].• Enfin 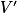 s'annule et change de signe lorsque x = 10, ce qui signifie que V admet un maximum égal à V(10) atteint lorsque x = 10.
s'annule et change de signe lorsque x = 10, ce qui signifie que V admet un maximum égal à V(10) atteint lorsque x = 10.
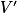 s'annule et change de signe lorsque x = 10, ce qui signifie que V admet un maximum égal à V(10) atteint lorsque x = 10.
s'annule et change de signe lorsque x = 10, ce qui signifie que V admet un maximum égal à V(10) atteint lorsque x = 10.• On calcule V(0) = 4 000 × 0 − 260 × 02 + 4 × 03 = 0. On calcule de la même manière V(10) et V(25).
On a donc le tableau de variations suivant :
On a donc le tableau de variations suivant :
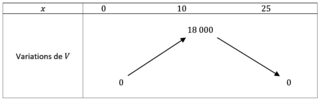 |
• Ainsi on peut en déduire que pour fabriquer une boîte avec le volume le plus grand possible, il faut choisir de découper des carrés dont les côtés ont pour longueur 10 cm dans les quatre coins des feuilles cartonnées en réserve. Le volume de la boîte (ouverte sur le dessus) sera de 18 000 cm3 (ou encore 18 dm3 c'est-à-dire 18 L).Exercice n°4Exercice n°5
Exercice n°1
Quel est le coefficient directeur de la tangente à la courbe représentative de la fonction carré au point E d'abscisse 10 ?
Cochez la bonne réponse.
| ||
| ||
| ||
|
Déterminons le nombre dérivé de la fonction carré en 10.
Si pour tout x de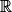 f(x) = x2, alors pour tout x de
f(x) = x2, alors pour tout x de 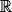
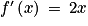 .
.
En particulier, on a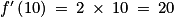 .
.
Ainsi le nombre dérivé de la fonction carré en 10 est 20.
Cela signifie que la courbe représentative de la fonction carré admet une tangente au point E d'abscisse 10 et que cette tangente possède un coefficient directeur égal à 20.
Si pour tout x de
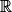 f(x) = x2, alors pour tout x de
f(x) = x2, alors pour tout x de 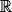
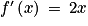 .
.En particulier, on a
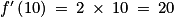 .
.Ainsi le nombre dérivé de la fonction carré en 10 est 20.
Cela signifie que la courbe représentative de la fonction carré admet une tangente au point E d'abscisse 10 et que cette tangente possède un coefficient directeur égal à 20.
Exercice n°2
On considère la fonction w définie sur 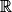 par
par 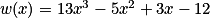 .
.
Quelle est l'expression de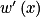 ?
?
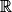 par
par 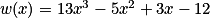 .
.Quelle est l'expression de
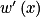 ?
? Cochez la bonne réponse.
| ||
| ||
| ||
|
On considère la fonction w définie sur 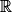 par
par 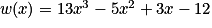 .
.
Déterminons l'expression de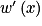 .
.
Pour tout x de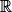 :
:
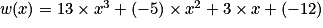
Donc pour tout x de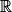 :
:
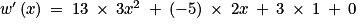
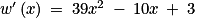
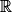 par
par 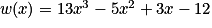 .
.Déterminons l'expression de
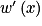 .
.Pour tout x de
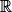 :
: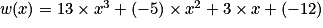
Donc pour tout x de
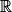 :
: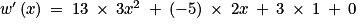
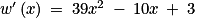
Exercice n°3
On considère la fonction m définie sur 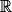 par
par 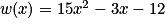 .
.
Sur quel intervalle la fonction m est-elle croissante ?
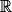 par
par 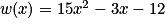 .
.Sur quel intervalle la fonction m est-elle croissante ?
Cochez la bonne réponse.
| ||
| ||
| ||
|
On considère la fonction m définie sur 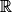 par
par 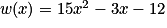 .
.
Pour tout x de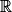 :
:
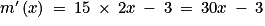
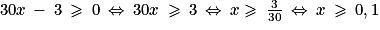
Ainsi on a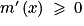 si et seulement si
si et seulement si 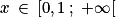 .
.
Donc la fonction m est croissante sur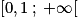 .
.
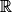 par
par 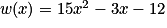 .
.Pour tout x de
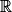 :
: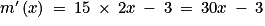
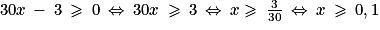
Ainsi on a
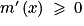 si et seulement si
si et seulement si 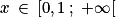 .
.Donc la fonction m est croissante sur
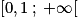 .
.Exercice n°4
On considère un système électrique dans lequel l'intensité du courant (en Ampères) varie entre 2A et 7A.
Soit la fonction P qui à l'intensité du courant x (en A) associe la puissance dissipée P(x) (en Watts) du courant. On admet que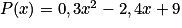
Quelle est l'expression de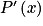 ?
?
Soit la fonction P qui à l'intensité du courant x (en A) associe la puissance dissipée P(x) (en Watts) du courant. On admet que
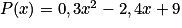
Quelle est l'expression de
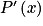 ?
? Cochez la bonne réponse.
| ||
| ||
| ||
|
Pour tout x de [2 ; 7] :
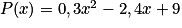
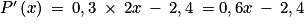 .
.
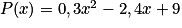
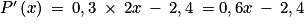 .
.Exercice n°5
On considère un système électrique dans lequel l'intensité du courant (en ampères) varie entre 2A et 7A.
Soit la fonction P qui à l'intensité du courant x (en A) associe la puissance dissipée P(x) (en watts) du courant. On admet que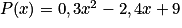
On admet que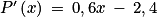 .
.
Quelle intensité du courant doit-on choisir si l'on souhaite que la puissance dissipée soit minimale ?
Soit la fonction P qui à l'intensité du courant x (en A) associe la puissance dissipée P(x) (en watts) du courant. On admet que
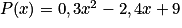
On admet que
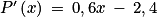 .
.Quelle intensité du courant doit-on choisir si l'on souhaite que la puissance dissipée soit minimale ?
Cochez la bonne réponse.
| ||
| ||
| ||
|
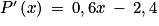
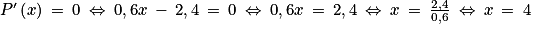
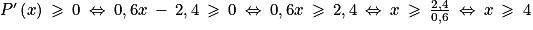
De la même manière
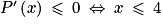 . Et
. Et ![4\: \in \: \left [2\: ; 7 \right ]](https://static1.assistancescolaire.com/1/images/1_sci_40_m123.png) .
.On a donc
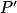 qui s'annule et change de signe lorsque x = 4. Donc P admet un minimum égal à P(4) atteint lorsque x = 4.
qui s'annule et change de signe lorsque x = 4. Donc P admet un minimum égal à P(4) atteint lorsque x = 4.Et
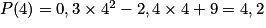
Ainsi il faut choisir une intensité de courant égale à 4 A pour que la puissance dissipée soit minimale et égale à 4,2 W.
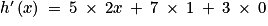
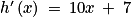
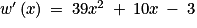
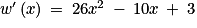
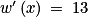
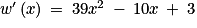
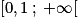
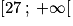
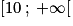
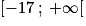
 + 2,4
+ 2,4 - 2,4
- 2,4 - 2,4
- 2,4 + 2,4
+ 2,4
