I. Dans quels types de situations utilise-t-on une suite géométrique ?
• Lorsque l'on observe un phénomène discret, si une grandeur change de valeur par étapes en étant toujours multipliée par un même nombre q, alors on pourra modéliser l'évolution de cette grandeur par une suite géométrique.
• Remarque : On a alors un taux d'évolution entre deux valeurs successives qui est constant et égal à q − 1.
II. Comment démontrer qu'une suite est géométrique ?
• Définition : On dit qu'une suite (un) définie sur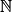 
est géométrique de raison q (q un réel) si et seulement si pour tout n de 
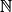on a : un+1 = un × q. On dit que c'est une relation de récurrence.
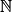est géométrique de raison q (q un réel) si et seulement si pour tout n de 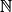on a : un+1 = un × q. On dit que c'est une relation de récurrence.• Exemple : L'INSEE estime que la population française était d'environ 67,8 millions d'habitants en 2022. On souhaite étudier la projection suivante : « La population française augmente de 3 % chaque année. » Pour cela, pour tout n de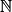 
on note pn la population française (en millions) en 2022 + n.
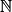on note pn la population française (en millions) en 2022 + n.• On a donc p0 = 67,8. Pour trouver la population en 2023, on doit donc calculer p1.
D'après l'énoncé :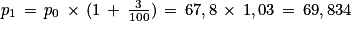
On a la relation de récurrence suivante :
Pour tout n de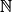
: pn+1 = pn × 1,03.
Donc la suite (pn) est géométrique de premier terme p0 = 67,8 et de raison q = 1,03.
Exercice n°1
D'après l'énoncé :
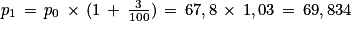
On a la relation de récurrence suivante :
Pour tout n de
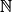: pn+1 = pn × 1,03.Donc la suite (pn) est géométrique de premier terme p0 = 67,8 et de raison q = 1,03.
Exercice n°1
III. Quelle est l'expression du terme général d'une suite arithmétique ?
• Propriété : Si (un) est une suite définie sur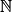 
et géométrique de raison q ( q un réel), alors pour tout n de 
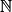on a : un = u0 × qn. On dit que c'est une relation fonctionnelle.
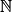et géométrique de raison q ( q un réel), alors pour tout n de 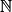on a : un = u0 × qn. On dit que c'est une relation fonctionnelle.• Exemple : Reprenons l'étude de la projection. La suite (pn) est géométrique de premier terme p0 = 67,8 et de raison q = 1,03. Ainsi pour tout n de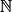 
: pn = p0 × qn = 67,8 × 1,03n.
Exercice n°2
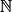: pn = p0 × qn = 67,8 × 1,03n.Exercice n°2
IV. Comment étudier le sens de variation d'une suite géométrique ?
• Propriété : Soit (un) une suite définie sur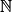 
et géométrique de raison q (q un réel). Dans le cas où u0 > 0 et q > 0, alors :
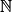et géométrique de raison q (q un réel). Dans le cas où u0 > 0 et q > 0, alors :- si q > 1, alors (un) est strictement croissante ;
- si q = 1, alors (un) est constante ;
- si 0 < q < 1, alors (un) est strictement décroissante.
• Exemple : Soit la suite (pn) est géométrique de premier terme p0 = 67,8 et de raison q = 1,03.
Comme 67,8 > 0 (premier terme strictement positif) et 1,03 > 1 (raison strictement supérieure à 1), alors (pn) est strictement croissante.
Exercice n°3
Comme 67,8 > 0 (premier terme strictement positif) et 1,03 > 1 (raison strictement supérieure à 1), alors (pn) est strictement croissante.
Exercice n°3
V. Comment représenter graphiquement une suite géométrique ?
On munit le plan d'un repère, de préférence orthogonal, voire orthonormé.• Définition : Soit (un) une suite définie sur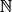 
et géométrique de raison q (q un réel), alors la représentation graphique de la suite est l'ensemble des points M de coordonnées M(n ; un).
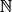et géométrique de raison q (q un réel), alors la représentation graphique de la suite est l'ensemble des points M de coordonnées M(n ; un).• Exemple 1 : Soit la suite (vn) est géométrique de premier terme v0 = 2 et de raison q = 3.
On a donc pour tout n de
: vn = 2 × 3n.
Donc v0 = 2 × 30 = 2 × 1 = 2 ; v1 = 2 × 31 = 2 × 3 = 6 ;
v2 = 2 × 32 = 18 ; v3 = 2 × 33 = 54.
Donc on va placer les premiers points de la représentation graphique de la suite (pn) : les points A(0 ; 2), B(1 ; 6), C(2 ; 18) et D(3 ; 54).
On a donc pour tout n de
: vn = 2 × 3n.Donc v0 = 2 × 30 = 2 × 1 = 2 ; v1 = 2 × 31 = 2 × 3 = 6 ;
v2 = 2 × 32 = 18 ; v3 = 2 × 33 = 54.
Donc on va placer les premiers points de la représentation graphique de la suite (pn) : les points A(0 ; 2), B(1 ; 6), C(2 ; 18) et D(3 ; 54).
 |
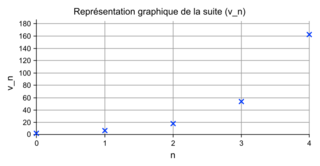• Remarque : On obtient un nuage de points et les points ne sont pas alignés (sauf dans le cas où q = 1).
• Exemple 2 : Soit la suite (wn) est géométrique de premier terme w0 = 100 et de raison q = 0,5.
On a donc pour tout n de
: vn = 100 × 0,5n.
Donc w0 = 100 × 0,50 = 100 × 1 = 100 ; w1 = 100 × 0,51 = 100 × 0,5 = 50 ;
w2 = 100 × 0,52 = 25 ; w3 = 100 × 0,53 = 12,5.
Donc on va placer les premiers points de la représentation graphique de la suite (pn) : les points A(0 ; 100), B(1 ; 50), C(2 ; 25) et D(3 ; 12,5).
On a donc pour tout n de
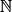: vn = 100 × 0,5n.Donc w0 = 100 × 0,50 = 100 × 1 = 100 ; w1 = 100 × 0,51 = 100 × 0,5 = 50 ;
w2 = 100 × 0,52 = 25 ; w3 = 100 × 0,53 = 12,5.
Donc on va placer les premiers points de la représentation graphique de la suite (pn) : les points A(0 ; 100), B(1 ; 50), C(2 ; 25) et D(3 ; 12,5).
 |
VI. Comment résoudre un problème de seuil ?
• Soit a, b et c trois réels (et a non nul).
• Pour déterminer le plus petit entier naturel n tel que : a × bn > c, on va utiliser un tableau de valeurs que l'on pourra créer grâce à une calculatrice ou bien un tableur.
On peut aussi utiliser un script du type :
On peut aussi utiliser un script du type :
 |
• Dans ce script :
- u0 est le premier terme de la suite géométrique ;
- q est la raison de la suite ;
- c est la valeur que l'on souhaite « dépasser ».
• Exemple : L'INSEE estime que la population française était d'environ 67,8 millions d'habitants en 2022.
On souhaite étudier la projection suivante : « La population française augmente de 3 % chaque année. »
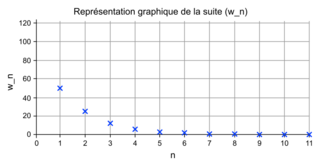
Pour cela, pour tout n de
on note pn la population française (en millions) en 2022 + n.
On a montré que pour tout n de
: pn = p0 × qn = 67,8 × 1,03n.
D'après la projection, à partir de quelle année la population française dépassera-t-elle 100 millions d'habitants ?
On souhaite étudier la projection suivante : « La population française augmente de 3 % chaque année. »
Pour cela, pour tout n de
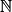on note pn la population française (en millions) en 2022 + n.On a montré que pour tout n de
: pn = p0 × qn = 67,8 × 1,03n.D'après la projection, à partir de quelle année la population française dépassera-t-elle 100 millions d'habitants ?
• On réalise un tableau de valeurs.
C'est-à-dire que l'on calcule p0, p1, p2 etc.
C'est-à-dire que l'on calcule p0, p1, p2 etc.
 |
• On observe que :p13 < 100 < p14.
De plus, on a prouvé précédemment que la suite (pn) est strictement croissante, donc le premier entier naturel n tel que pn > 100 est 14.
Cela signifie qu'en 2022+14, c'est-à-dire en 2036, la population française aura pour la première fois dépassée les 100 millions d'habitants d'après la projection proposée.
Exercice n°5
De plus, on a prouvé précédemment que la suite (pn) est strictement croissante, donc le premier entier naturel n tel que pn > 100 est 14.
Cela signifie qu'en 2022+14, c'est-à-dire en 2036, la population française aura pour la première fois dépassée les 100 millions d'habitants d'après la projection proposée.
Exercice n°5
Exercice n°1
Amandine entretient la pelouse de son jardin qui a une superficie de 750 m2.
Chaque mois la pelouse perd 2 % de sa surface.
Pour tout n de
, on note sn la surface de la pelouse au bout de n mois.
Quelle est la nature de la suite (sn) ?
Chaque mois la pelouse perd 2 % de sa surface.
Pour tout n de
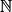, on note sn la surface de la pelouse au bout de n mois.Quelle est la nature de la suite (sn) ?
Cochez la bonne réponse.
| ||
| ||
| ||
|
Diminuer une quantité de 2 % revient à multiplier cette quantité par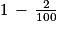 
Pour tout entier naturel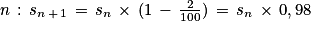
Ainsi la suite (sn) est géométrique de raison q = 0,98.
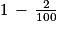
Pour tout entier naturel
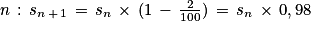
Ainsi la suite (sn) est géométrique de raison q = 0,98.
Exercice n°2
Amandine entretient la pelouse de son jardin qui a une aire de 750 m2.
Chaque mois la pelouse perd 2 % de sa surface.
Pour tout n de
, on note sn l'aire de la pelouse (en m2) au bout de n mois.
On admet que (sn) est géométrique de raison q = 0,98.
Quelle est l'expression de sn en fonction de n ?
Chaque mois la pelouse perd 2 % de sa surface.
Pour tout n de
, on note sn l'aire de la pelouse (en m2) au bout de n mois.On admet que (sn) est géométrique de raison q = 0,98.
Quelle est l'expression de sn en fonction de n ?
Cochez la bonne réponse.
| ||
| ||
| ||
|
La suite (sn) est géométrique de raison q = 0,98.
Le premier terme est s0 et il est égal à 750.
En effet s0 est l'aire de la pelouse (en m2) au bout de 0 mois, c'est-à-dire au début de l'histoire.
Ainsi pour tout entier naturel n : sn = s0 × qn = 750 × 0,98n.
Le premier terme est s0 et il est égal à 750.
En effet s0 est l'aire de la pelouse (en m2) au bout de 0 mois, c'est-à-dire au début de l'histoire.
Ainsi pour tout entier naturel n : sn = s0 × qn = 750 × 0,98n.
Exercice n°3
Amandine entretient la pelouse de son jardin qui a une aire de 750 m2.
Chaque mois la pelouse perd 2 % de sa surface.
Pour tout n de
, on note sn l'aire de la pelouse (en m2) au bout de n mois.
On admet que (sn) est géométrique de raison q = 0,98.
Quel est le sens de variation de la suite (sn) ?
Chaque mois la pelouse perd 2 % de sa surface.
Pour tout n de
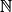, on note sn l'aire de la pelouse (en m2) au bout de n mois.On admet que (sn) est géométrique de raison q = 0,98.
Quel est le sens de variation de la suite (sn) ?
Cochez la bonne réponse.
| ||
| ||
| ||
|
La suite (sn) est géométrique de raison q = 0,98.
Le premier terme est s0 et il est égal à 750.
On a donc s0 > 0 et 0 < q < 1. Donc la suite (sn) est strictement décroissante.
Le premier terme est s0 et il est égal à 750.
On a donc s0 > 0 et 0 < q < 1. Donc la suite (sn) est strictement décroissante.
Exercice n°4
On admet que pour tout entier naturel n : sn = 750 × 0,98n.
Déterminer le seul point proposé appartenant à la représentation graphique de la suite (sn).
Déterminer le seul point proposé appartenant à la représentation graphique de la suite (sn).
Cochez la bonne réponse.
| ||
| ||
| ||
|
s0 = s0 × q0 = 750 × 0,980 = 750 × 1 = 750.
Donc le point de coordonnées (0 ; 0) n'appartient pas à la représentation graphique de (sn) :
s2 = s0 × q2 = 750 × 0,982 = 750 × 0,9604 = 720,3.
Donc le point de coordonnées (2 ; 720,3) appartient à la représentation graphique de (sn).
Donc le point de coordonnées (0 ; 0) n'appartient pas à la représentation graphique de (sn) :
s2 = s0 × q2 = 750 × 0,982 = 750 × 0,9604 = 720,3.
Donc le point de coordonnées (2 ; 720,3) appartient à la représentation graphique de (sn).
Exercice n°5
Amandine entretient la pelouse de son jardin qui a une aire de 750 m2.
Chaque mois la pelouse perd 2 % de sa surface.
Pour tout n de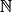
, on note sn l'aire de la pelouse (en m2) au bout de n mois.
On admet que pour tout entier naturel n : sn = 750 × 0,98n.
Au bout de combien de mois la pelouse aura-t-elle une aire inférieure à 600 m2 ?
Chaque mois la pelouse perd 2 % de sa surface.
Pour tout n de
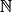, on note sn l'aire de la pelouse (en m2) au bout de n mois.On admet que pour tout entier naturel n : sn = 750 × 0,98n.
Au bout de combien de mois la pelouse aura-t-elle une aire inférieure à 600 m2 ?
Cochez la bonne réponse.
| ||
| ||
| ||
|
On doit déterminer le plus petit entier naturel n, tel que :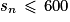 
.
On va utiliser un tableau de valeurs.
Dans la cellule B2, on a entré la formule suivante :
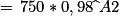
puis on a utilisé la poignée de recopie vers le bas.
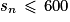.On va utiliser un tableau de valeurs.
Dans la cellule B2, on a entré la formule suivante :
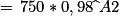
puis on a utilisé la poignée de recopie vers le bas.
 |
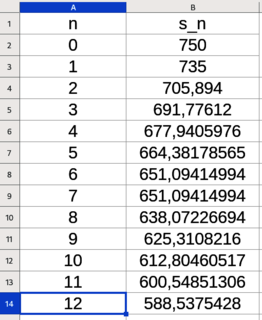On remarque que :
s12 < 600 < s11
De plus, on a montré que la suite (sn) est strictement décroissante.
Ainsi le premier entier naturel n, tel que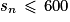
, est 12.
Cela signifie qu'après 12 mois (ou un an), la pelouse aura une aire inférieure à 600 m2.
On pouvait aussi utiliser un script comme :
s12 < 600 < s11
De plus, on a montré que la suite (sn) est strictement décroissante.
Ainsi le premier entier naturel n, tel que
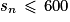, est 12.Cela signifie qu'après 12 mois (ou un an), la pelouse aura une aire inférieure à 600 m2.
On pouvait aussi utiliser un script comme :
 |
En tapant le nom de la fonction dans la console, on obtient bien 12.
 |
