Protection des crapauds, sujet de métropole, mars 2023, exercice 2
Énoncé
Exercice sur 5 points
La plaine de Sorques, située dans le sud de la Seine-et-Marne, est une zone naturelle protégée qui abrite entre autres de nombreux amphibiens (crapauds, grenouilles, tritons). Les crapauds Bufo bufo ont pour habitat la forêt de Fontainebleau la majeure partie de l'année. Une fois par an, au printemps, ces amphibiens migrent vers les plans d'eau pour se reproduire.
La plaine de Sorques, située dans le sud de la Seine-et-Marne, est une zone naturelle protégée qui abrite entre autres de nombreux amphibiens (crapauds, grenouilles, tritons). Les crapauds Bufo bufo ont pour habitat la forêt de Fontainebleau la majeure partie de l'année. Une fois par an, au printemps, ces amphibiens migrent vers les plans d'eau pour se reproduire.
 Barrière de protection le long d'une route |
Pour éviter qu'ils ne se fassent écraser en passant sur la route qui traverse cette zone de migration, un dispositif a été installé : des barrières en bois, suffisamment hautes pour empêcher le saut sur la route, sont placées de chaque côté, obligeant les amphibiens à emprunter des passages souterrains appelés « crapauducs ».
Dans cet exercice, on se propose d'étudier le mouvement lors d'un saut d'un crapaud Bufo bufo de façon à déterminer la hauteur minimale des barrières de protection le long d'une route.
Le système considéré est un crapaud dont on étudie le mouvement du centre de masse, noté G. Le champ de pesanteur terrestre local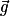 est considéré comme uniforme et les frottements liés à l'action de l'air sont supposés négligeables face au poids.
est considéré comme uniforme et les frottements liés à l'action de l'air sont supposés négligeables face au poids.
Dans cet exercice, on se propose d'étudier le mouvement lors d'un saut d'un crapaud Bufo bufo de façon à déterminer la hauteur minimale des barrières de protection le long d'une route.
Le système considéré est un crapaud dont on étudie le mouvement du centre de masse, noté G. Le champ de pesanteur terrestre local
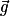 est considéré comme uniforme et les frottements liés à l'action de l'air sont supposés négligeables face au poids.
est considéré comme uniforme et les frottements liés à l'action de l'air sont supposés négligeables face au poids.Données :
• intensité de la pesanteur terrestre : g = 9,81 m·s−2 ;
• taille moyenne d'un crapaud Bufo bufo : 10 cm.
Le mouvement du centre de masse G du crapaud est étudié dans le référentiel terrestre supposé galiléen et muni du système d'axes (Ox, Oz), respectivement horizontal muni du vecteur unitaire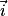 et vertical muni du vecteur unitaire
et vertical muni du vecteur unitaire 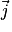 voir figure 1).
voir figure 1).
Le mouvement du centre de masse G du crapaud est étudié dans le référentiel terrestre supposé galiléen et muni du système d'axes (Ox, Oz), respectivement horizontal muni du vecteur unitaire
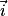 et vertical muni du vecteur unitaire
et vertical muni du vecteur unitaire 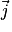 voir figure 1).
voir figure 1).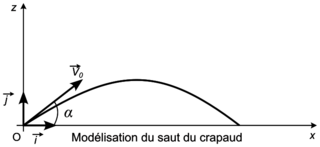 Figure 1. Modélisation du saut du crapaud |
À la date t = 0 s, le centre de masse G est placé à l'origine du repère O et son vecteur vitesse initiale, noté 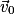 , a une direction faisant un angle α avec l'axe horizontal (Ox). On note v0 la norme de
, a une direction faisant un angle α avec l'axe horizontal (Ox). On note v0 la norme de 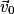 .
.
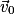 , a une direction faisant un angle α avec l'axe horizontal (Ox). On note v0 la norme de
, a une direction faisant un angle α avec l'axe horizontal (Ox). On note v0 la norme de 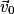 .
.Q1. Établir les expressions littérales des composantes ax et az du vecteur accélération 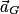 du centre de masse du crapaud suivant les axes (Ox) et (Oz).
du centre de masse du crapaud suivant les axes (Ox) et (Oz).
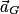 du centre de masse du crapaud suivant les axes (Ox) et (Oz).
du centre de masse du crapaud suivant les axes (Ox) et (Oz).Le crapaud est en chute libre, il n'est donc soumis qu'à son poids qui est une force verticale. Déterminez les composantes du vecteur accélération avec la deuxième loi de Newton.
Q2. Établir les expressions littérales des composantes vx(t) et vz(t) du vecteur vitesse 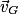 du centre de masse du crapaud suivant les axes (Ox) et (Oz).
du centre de masse du crapaud suivant les axes (Ox) et (Oz).
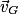 du centre de masse du crapaud suivant les axes (Ox) et (Oz).
du centre de masse du crapaud suivant les axes (Ox) et (Oz).Déterminez les primitives de chaque composante du vecteur accélération de la question précédente. Attention à tenir compte des composantes de la vitesse initiale du crapaud.
Q3. Montrer que les expressions littérales des équations horaires x(t) et z(t) de la position du centre de masse G du crapaud au cours de son mouvement s'écrivent :
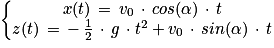
Déterminez les primitives de chaque composante du vecteur position du centre de masse G du crapaud de la question précédente.
Q4. Établir l'expression de la durée du saut du crapaud, notée tsaut, en fonction de v0, g, et α.
Avec une des deux équations horaires, isolez la durée.
Q5. En utilisant l'expression de x(t) et l'expression de tsaut obtenue à la réponse à la question Q4, montrer que la vitesse v0 permettant au crapaud d'effectuer un saut de longueur d est donnée par la relation :
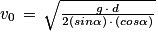
La question fait appel à plusieurs relations trouvées précédemment qu'il faut combiner pour déterminer la vitesse v0.
Q6. Sachant que les crapauds les plus puissants peuvent faire des sauts d'une longueur égale à 20 fois leur taille, calculer la valeur de v0 qu'ils atteignent pour un angle α = 45° .
Il s'agit ici d'une simple application numérique.
La hauteur maximale zmax d'un saut est obtenue lorsque ce saut est vertical ; l'angle α vaut alors α = 90°, la vitesse initiale est toujours notée v0.
Q7. Établir que la hauteur maximale d'un saut a pour expression littérale :
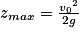
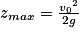
Déterminez dans un premier temps la durée nécessaire à réaliser la hauteur maximale. Ce point correspond au sommet de la parabole.
Q8. En déduire la valeur de la hauteur de barrière minimale, notée Hchampion, qui permet d'arrêter les crapauds les plus puissants, capables de sauter verticalement avec une vitesse initiale v0 de valeur calculée à la question Q6.
Calculez la hauteur maximale avec la relation précédente. Puis comparez à la hauteur de la barrière.
Q9. Les barrières mesurent en réalité 50 à 60 cm de hauteur. Donner un argument permettant d'expliquer pourquoi on choisit d'installer des barrières d'une hauteur inférieure à Hchampion.
Lors de l'étude du saut du crapaud, on a posé des hypothèses sur le saut. Il est donc nécessaire de vérifier à présent la justesse de ses hypothèses.
Corrigé
Q1. Système{Crapaud} de masse m et de centre de masse G.
Référentiel terrestre supposé galiléen.
Le crapaud n'est soumis qu'à son poids.
La deuxième loi de Newton se résume alors à :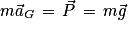 .
.
Soit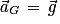
Dans le repère choisi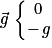 d'où
d'où 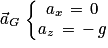
Référentiel terrestre supposé galiléen.
Le crapaud n'est soumis qu'à son poids.
La deuxième loi de Newton se résume alors à :
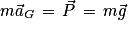 .
.Soit
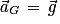
Dans le repère choisi
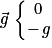 d'où
d'où 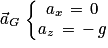
Q2. La vitesse du crapaud :
Comme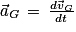 alors
alors 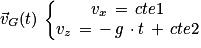
Les constantes cte1 et cte2 sont déterminées par les conditions initiales :
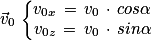 et
et 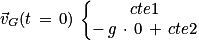 d'où
d'où 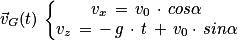
Comme
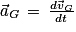 alors
alors 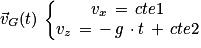
Les constantes cte1 et cte2 sont déterminées par les conditions initiales :
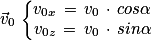 et
et 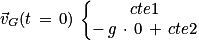 d'où
d'où 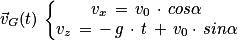
Q3. Les équations du mouvement du crapaud :
Comme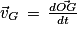 alors
alors 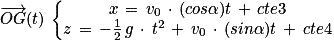
Les constantes cte3 et cte4 sont déterminées par les conditions initiales :
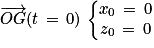 et
et 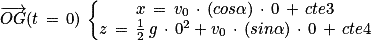 d'où
d'où 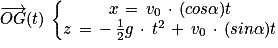
Comme
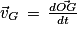 alors
alors 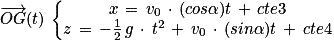
Les constantes cte3 et cte4 sont déterminées par les conditions initiales :
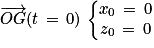 et
et 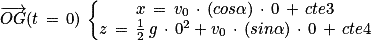 d'où
d'où 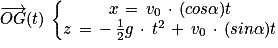
Q4. La durée du saut du crapaud : lorsque le crapaud retombe z(t) = 0
Donc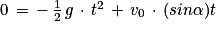
D'où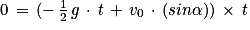
Soit t = 0 (départ du crapaud)
Soit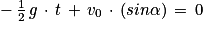 , d'où
, d'où 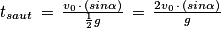
Donc
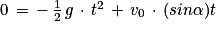
D'où
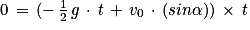
Soit t = 0 (départ du crapaud)
Soit
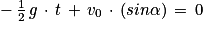 , d'où
, d'où 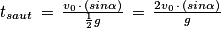
Q5. Lorsque le crapaud a sauté, il a parcouru une distance telle que x = d.
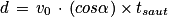 , d'où
, d'où 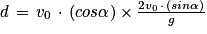
Soit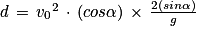
D'où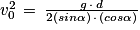
Finalement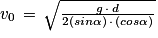
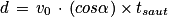 , d'où
, d'où 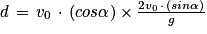
Soit
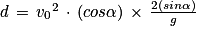
D'où
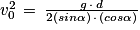
Finalement
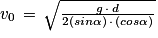
Q6. Application numérique :
On a d = 20 × 10 = 2 m.
Et v0 = 4,4 m·s−1.
On a d = 20 × 10 = 2 m.
Et v0 = 4,4 m·s−1.
Q7. La hauteur maximale est obtenue lorsque l'angle α = 90°, donc sin(90) = 1. Au sommet, la tangente à la trajectoire et donc le vecteur vitesse sont horizontaux, d'où :
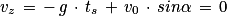 , d'ou
, d'ou 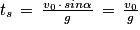
Dans la relation donnant z, on a alors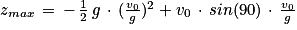
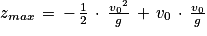
Donc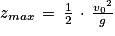
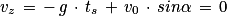 , d'ou
, d'ou 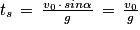
Dans la relation donnant z, on a alors
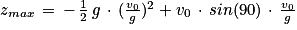
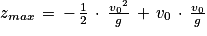
Donc
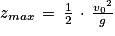
Q8. Application numérique avec la valeur de v0 de la question 6. zmax = 1 m.
Il suffit de mettre une barrière d'une hauteur Hchampion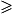 zmax, soit Hchampion
zmax, soit Hchampion 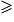 1 m.
1 m.
Il suffit de mettre une barrière d'une hauteur Hchampion
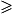 zmax, soit Hchampion
zmax, soit Hchampion 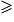 1 m.
1 m.Q9. Les barrières sont plus petites dans la réalité, car les crapauds ne sautent pas verticalement donc l'angle choisi de 90° n'est pas vrai dans la réalité, l'altitude maximale atteinte par le crapaud est inférieure à 1 m.
De plus, seuls les crapauds les plus puissants peuvent atteindre Hchampion = 1 m de haut, ce qui n'est pas le cas de tous les crapauds.
De plus, seuls les crapauds les plus puissants peuvent atteindre Hchampion = 1 m de haut, ce qui n'est pas le cas de tous les crapauds.

