Sujet national, juin 2025, exercice 4

Énoncé

Exercice sur 6 points
L'objet de cet exercice est l'étude de l'arrêt d'un chariot sur un manège, à partir du moment où il entre dans la zone de freinage en fin de parcours.
On note t le temps écoulé, exprimé en secondes, à partir du moment où le chariot arrive sur la zone de freinage.
On modélise la distance parcourue par le chariot dans la zone de freinage, exprimée en mètres, en fonction de t, à l'aide d'une fonction notée d définie sur [0 ;+∞[.
On a ainsi d(0) = 0.
Par ailleurs, on admet que cette fonction d est dérivable sur son ensemble de définition. On note d' sa fonction dérivée.

Partie A

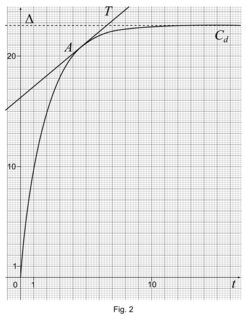
Sur la figure (fig. 2) ci-dessous, on a tracé dans un repère orthonormé :

• la courbe représentative C_d de la fonction d ;

• la tangente T à la courbe C_d au point A d'abscisse 4,7 ;

• l'asymptote Δ à C_d en +∞.

Dans cette partie, aucune justification n'est attendue.
Avec la précision que permet le graphique, répondre aux questions ci-dessous.
D'après ce modèle :

1. Au bout de combien de temps le chariot aura-t-il parcouru 15 m dans la zone de freinage ?

2. Quelle longueur minimale doit-être prévue pour la zone de freinage ?

3. Que vaut d'(4,7) ? Interpréter ce résultat dans le contexte de l'exercice.

Partie B

On rappelle que t désigne le temps écoulé, en secondes, à partir du moment où le chariot arrive sur la zone de freinage.
On modélise la vitesse instantanée du chariot, en mètres par seconde (m.s⁻¹), en fonction de t, par une fonction v définie sur [0 ; +∞[.
On admet que :

• la fonction v est dérivable sur son ensemble de définition, et on note v' sa fonction dérivée ;

• la fonction v est une solution de l'équation différentielle (E) :
y' + 0,6y = e^−0,6t,
où y est une fonction inconnue et où y' est la fonction dérivée de y.
On précise de plus que, lors de son arrivée sur la zone de freinage, la vitesse du chariot est égale à 12 m.s⁻¹, c'est-à-dire v(0) = 12.

1. a. On considère l'équation différentielle (E') : y' + 0,6y = 0.
Déterminer les solutions de l'équation différentielle (E') sur [0 ; +∞[.

b. Soit g la fonction définie sur [0 ; +∞[ par g(t) = te^−0,6t.
Vérifier que la fonction g est une solution de l'équation différentielle (E).

c. En déduire les solutions de l'équation différentielle (E) sur [0 ; +∞[.

d. En déduire que pour tout réel t appartenant à l'intervalle [0 ; +∞[, on a :
v(t) = (12 + t)e^−0,6t.

Dans cette question, on étudie la fonction v sur [0 ; +∞[.

2. a. Montrer que pour tout réel $t\: \in \: \left [ 0\: ;+\infty \right ],\: {v}'\left ( t \right )\: =\: \left ( -6,2\: -0,6t \right )e^{-0,6t}$

b. En admettant que :
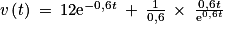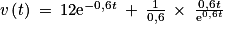$v\left ( t \right )\: =\: 12\textrm{e}^{-0,6t}\: +\: \frac{1}{0,6}\: \times \: \frac{0,6t}{\textrm{e}^{0,6t}}$ , déterminer la limite de v en +∞.

c. Étudier le sens de variation de la fonction v et dresser son tableau de variation complet. Justifier.

d. Montrer que l'équation v(t) = 1 admet une solution unique α, dont on donnera une valeur approchée au dixième.

3. Lorsque la vitesse du chariot est inférieure ou égale à 1 mètre par seconde, un système mécanique se déclenche, permettant son arrêt complet. Déterminer au bout de combien de temps ce système entre en action. Justifier.

Partie C

On rappelle que pour tout réel t appartenant à l'intervalle [0 ; +∞[ :
v(t) = (12 + t)e^−0,6t.
On admet que pour tout réel t dans l'intervalle [0 ; +∞[ :
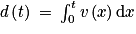$d\left ( t \right )\: =\: \int_{0}^{t}v\left ( x \right )\textrm{d}x$ .

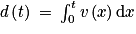1. À l'aide d'une intégration par parties, montrer que la distance parcourue par le chariot entre les instants 0 et t est donnée par :
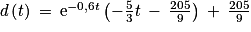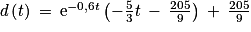$d\left ( t \right )\: =\: \textrm{e}^{-0,6t}\left ( -\frac{5}{3}t\: -\: \frac{205}{9} \right )\: +\: \frac{205}{9}$ .

2. On rappelle que le dispositif d'arrêt se déclenche lorsque la vitesse du chariot est inférieure ou égale à 1 mètre par seconde. Déterminer, selon ce modèle, une valeur approchée au centième de la distance parcourue par le chariot dans la zone de freinage avant le déclenchement de ce dispositif.

Corrigé

Partie A

t : temps en secondes
d(t) : distance en mètres

1. On cherche à résoudre d(t) = 15.
Les solutions sont les abscisses des points d'intersection entre C_d et la droite d'équation y = 15. Ici on constate un seul point d'intersection, qui possède une abscisse égale à environ 2. Ainsi, le chariot aura parcouru une distance de 15 m dans la zone de freinage au bout de 2 secondes.

2. On constate que l'asymptote Δ à C_d en +∞ a pour équation y = 22,8.
Donc :
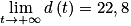
$\displaystyle \lim_{t \to +\infty }d\left ( t \right )=22,8$
De plus, il semblerait que la fonction d soit strictement croissante sur [0 ;+∞[.
On pourrait donc conjecturer que pour tout t de [0 ;+∞[, d(t) inférieur ou égal

22,8.
Ainsi, on devrait prévoir une distance de freinage d'au moins 23 m.

3. d' (4,7) est le coefficient directeur de la tangente T à C_d au point A d'abscisse 4,7 et d'ordonnée 20,8 (obtenue par lecture graphique). T semble couper l'axe des ordonnées au point B(0 ;16,5).
Donc :
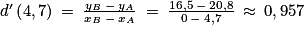
${d}'\left ( 4,7 \right )\: =\: \frac{y_{B}\: -\: y_{A}}{x_{B}\: -\: x_{A}}\: =\: \frac{16,5\: -\: 20,8}{0\: -\: 4,7}\: \approx \: 0,957$
On peut interpréter d'(4,7) comme la vitesse instantanée du chariot (en m.s⁻¹) à l'instant t = 4,7 s.
Ainsi, au bout de exactement 4,7 s, le chariot a une vitesse d'environ 0,957 m.s⁻¹.

Partie B

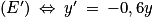
1. a. $\left ( {E}' \right )\: \Leftrightarrow \: {y}'\: =\: -0,6y$
Les solutions de (E') sont toutes les fonctions f_k définies pour tout t de [0 ;+∞[ par :
f_k (t) = ke^−0,6t avec k un réel

b. On va calculer l'expression g'(t) + 0,6 × g(t).
g est dérivable sur [0 ;+∞[ et pour tout t de [0 ;+∞[ g(t) = a(t) × b(t), avec a(t) = t et b(t) = e^−0,6t. Les fonctions a et b sont dérivables sur [0 ;+∞[ et pour tout t de [0 ;+∞[ : a'(t) = 1 et b'(t) = −0,6e^−0,6t.
On a donc pour tout t de [0 ;+∞[ :
g'(t) = a'(t) × b(t) + b'^(t) × a(t)
g'(t) = 1 × e^−0,6t + (−0,6e^−0,6t) × t
g'(t) = e^−0,6t − 0,6te^−0,6t
Donc :
g'(t) + 0,6g(t) = e^−0,6t − 0,6te^−0,6t + 0,6te^−0,6t = e^−0,6t
Donc la fonction g est une solution de l'équation différentielle (E).

c. (E') est l'équation homogène associée à (E).
Donc les solutions de l'équation différentielle (E) sont les fonctions h_k définies pour tout t de [0 ;+∞[ par :
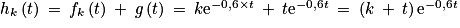$h_{k}\left ( t \right )\: =\: f_{k}\left ( t \right )\: +\: g\left ( t \right )\: =\: k\textrm{e}^{-0,6\times t}\: +\: t\textrm{e}^{-0,6t}\: =\: \left ( k\: +\: t \right )\textrm{e}^{-0,6t}$ avec k un réel.

d. v est solution de (E), donc il existe un réel particulier k₁ tel que pour tout t de [0 ;+∞[ :
v(t) = (k₁ + t)^−0,6t
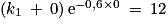De plus, v(0) = 12, donc $\left ( k_{1}\: +\: 0 \right )\textrm{e}^{-0,6\times 0}\: =\: 12$ . On a donc k₁ = 12.
Ainsi, pour tout t de [0 ;+∞[, v(t) = (12 + t)e^−0,6t.

2. a. v est dérivable sur [0 ;+∞[ et pour tout t de [0 ;+∞[ v(t) = p(t) × q(t),
avec p(t) = 12 + t et q(t) = e^−0,6t. Les fonctions p et q sont dérivables sur [0 ;+∞[ et pour tout t de [0 ;+∞[ : p'(t) = 1 et q'(t) = −0,6e^−0,6t.
On a, pour tout t de [0 ;+∞[ :
v'(t) = p'(t) × q(t) + q'^(t) × p(t).
v'(t) = 1 × e^−0,6t + (−0,6e^−0,6t) × (12 + t) = e^−0,6t − 0,6(12 + t)e^−0,6t.
On peut factoriser la somme par le facteur commun e^−0,6t.
v'(t) = e^−0,6t × (1 − 0,6(12 + t))
v'(t) = e^−0,6t × (1 − 7,2 − 0,6t)
v'(t) = (−6,2 − 0,6t)e^−0,6t

b. D'une part :
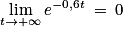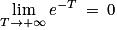
$\displaystyle \lim_{t \to +\infty }e^{-0,6t}\: =\: 0$ , car $\displaystyle \lim_{T \to +\infty }e^{-T}\: =\: 0$
D'autre part :
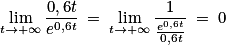
$\displaystyle \lim_{t \to +\infty }{\frac{0,6t}{e^{0,6t}}}\: =\: \displaystyle \lim_{t \to +\infty }\frac{1}{\frac{e^{0,6t}}{0,6t}}\: =\: 0$
En effet, par croissances comparées, on a :
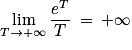
$\displaystyle \lim_{T \to +\infty }\frac{e^{T}}{T}\: =\: +\infty$
Ainsi, par somme et produit, on a :
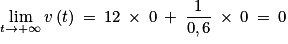
$\displaystyle \lim_{t \to +\infty }v\left ( t \right )\: =\: 12\: \times \: 0\: +\: \frac{1}{0,6}\: \times \: 0\: =\: 0$

Ainsi, la vitesse instantanée du chariot va à long terme se stabiliser vers 0 m/s, c'est-à-dire que le chariot va s'arrêter.

c. Pour étudier le sens de variation de la fonction v, il faut étudier le signe de la fonction v'.
On a, pour tout t de [0 ;+∞[ : v'(t) = (−6,2 − 0,6t)e^−0,6t.
Pour tout t de [0 ;+∞[, −0,6t inférieur ou égal

0, donc −6,2 − 0,6t inférieur ou égal

0.
De plus, e^−0,6t > 0.
Ainsi, par produit, pour tout t de [0 ;+∞[, v'(t) < 0.
Donc la fonction v' est strictement négative sur [0 ;+∞[, et on en déduit que la fonction v est strictement décroissante sur [0 ;+∞[.

d. La fonction v est continue sur [0 ;+∞[ car v est dérivable sur [0 ;+∞[.
La fonction v est strictement décroissante sur [0 ;+∞[.
$1\: \in \: \left [ 0\: ; 12 \right ]$
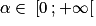Donc, d'après le corollaire du théorème des valeurs intermédiaires (on le surnomme parfois le théorème de la bijection), l'équation v(t) = 1 admet une unique solution sur [0 ;+∞[. On note cette solution α. On sait que $\alpha \in \: \left [ 0\: ;+\infty \right [$ .
D'après la calculatrice v(4,6) > 1 et v(4,7) < 1.
De plus, v(4,69) > 1 et v(4,70) < 1.
Donc, la valeur arrondie au dixième de α est 4,7.

3. On doit résoudre dans [0 ;+∞[ l'inéquation v(t) inférieur ou égal

1.
On sait que v est strictement décroissante sur [0 ;+∞[ et que v(α) = 1.
Donc :
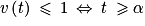
$v\left ( t \right )\: \leq \: 1\: \Leftrightarrow \: t\: \geq \alpha$
Ainsi, l'ensemble solution de l'inéquation est S = [ α;+∞[.
Ainsi, le système entre en action au bout de environ 4,7 secondes.

Partie C

1. Soit t un réel de [0 ;+∞[.
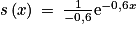On pose pour tout x de [0 ;t] v(x) = r(x) × s'(x), avec r(x) = 12 + x et s'^(x) = e^−0,6x. Les fonctions r et s sont dérivables sur [0 ;t]. Pour tout x de [0 ;t], on a r'(x) = 1 et $s\left ( x \right )\: =\: \frac{1}{-0,6}\textrm{e}^{-0,6x}$ .
Ainsi, grâce à une intégration par parties, on obtient :
$d\left ( t \right )\: =\: \int_{0}^{t}v\left ( x \right )dx\: =\: \int_{0}^{t}r\left ( x \right )\: \times \: {s}'\left ( x \right )dx\: =\: \left [ r\left ( x \right ) \: \times \: s\left ( x \right )\right ]_{0}^{t}\: -\: \int_{0}^{t}{r}'\left ( x \right )\: \times \: s\left ( x \right )dx$
$d\left ( t \right )\: =\: \left [ \left ( 12\: +\: x \right ) \: \times \: \frac{1}{-0,6}\textrm{e}^{-0,6x}\right ]_{0}^{t}\: -\: \int_{0}^{t}1\: \times \: \frac{1}{-0,6}\textrm{e}^{-0,6x}dx$
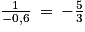
On remarque que $\frac{1}{-0,6}\: =\: -\frac{5}{3}$
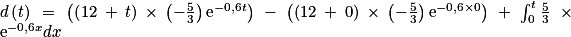
$d\left ( t\right )\: =\: \left ( \left ( 12\: +\: t \right )\: \times \: \left ( -\frac{5}{3} \right )\textrm{e} ^{-0,6t}\right )\: -\: \left ( \left ( 12\: +\: 0 \right )\: \times \: \left ( -\frac{5}{3} \right ) \textrm{e}^{-0,6\times 0}\right )\: +\: \int_{0}^{t}\frac{5}{3}\: \times \: \textrm{e}^{-0,6x}dx$
$d\left ( t\right )\: =\: \left ( \left ( 12\: +\: t \right )\: \times \: \left ( -\frac{5}{3} \right )\textrm{e} ^{-0,6t}\right )\: +\: 20\: +\: \left [ \frac{5}{3}\: \times \: \left ( -\frac{5}{3} \right )\textrm{e} ^{-0,6x}\right ]_{0}^{t}$
$d\left ( t\right )\: =\: \left ( -20\: -\: \frac{5}{3}t \right )\textrm{e}^{-0,6t}\: +\: 20\: -\: \frac{25}{9}\left [ \textrm{e}^{-0,6x} \right ]_{0}^{t}$
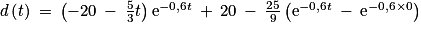
$d\left ( t\right )\: =\: \left ( -20\: -\: \frac{5}{3}t \right )\textrm{e}^{-0,6t}\: +\: 20\: -\: \frac{25}{9}\left ( \textrm{e}^{-0,6t}\: -\: \textrm{e}^{-0,6\times 0} \right )$
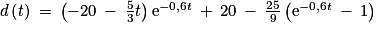
$d\left ( t\right )\: =\: \left ( -20\: -\: \frac{5}{3}t \right )\textrm{e}^{-0,6t}\: +\: 20\: -\: \frac{25}{9}\left ( \textrm{e}^{-0,6t} \: -\: 1\right )$
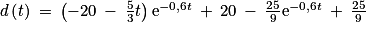
$d\left ( t\right )\: =\: \left ( -20\: -\: \frac{5}{3}t \right )\textrm{e}^{-0,6t}\: +\: 20\: -\: \frac{25}{9}\textrm{e}^{-0,6t}\: +\: \frac{25}{9}$
On factorise deux termes par e^−0,6t.
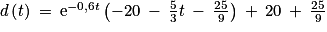
$d\left ( t\right )\: =\: \textrm{e}^{-0,6t}\left ( -20\: -\: \frac{5}{3}t\: -\: \frac{25}{9} \right )\: +\: 20\: +\: \frac{25}{9}$
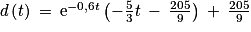
$d\left ( t\right )\: =\: \textrm{e}^{-0,6t}\left ( -\frac{5}{3}t\: -\: \frac{205}{9} \right )\: +\: \frac{205}{9}$

2. On sait que le dispositif de freinage se déclenche à t = α secondes.
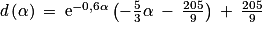La distance alors parcourue sera donc $d\left ( \alpha \right )\: =\: \textrm{e}^{-0,6\alpha }\left ( -\frac{5}{3}\alpha \: -\: \frac{205}{9} \right )\: +\: \frac{205}{9}$ .
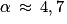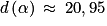En utilisant $\alpha \: \approx \: 4,7$ , on trouve $d\left ( \alpha \right )\: \approx \: 20,95$ .
Donc une valeur approchée de la distance parcourue par le chariot dans la zone de freinage avant le déclenchement de ce dispositif est environ 20,95 m.

On retrouve également cette approximation en allant lire l'ordonnée du point de la courbe C_d qui a pour abscisse 4,7 : c'est le point A.

Sujet national, juin 2025, exercice 4

Énoncé

Partie A

Partie B

Partie C

Annexes

Corrigé

Partie A

Partie B

Partie C