Sujet de métropole, juin 2024, exercice 3
Énoncé
Exercice sur 6 points
On considère une fonction f définie et deux fois dérivable sur ![\left ]-2\, ;\: +\infty \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde34_m1.png) . On note Cf sa courbe représentative dans un repère orthogonal du plan,
. On note Cf sa courbe représentative dans un repère orthogonal du plan, 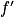 se dérivée et
se dérivée et 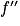 sa dérivée seconde.
sa dérivée seconde.
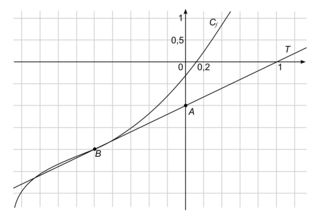
On a tracé ci-dessous la courbe Cf et sa tangente T au point B d'abscisse −1.
On précise que la droite T passe par le point A(0 ; −1).
![\left ]-2\, ;\: +\infty \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde34_m1.png) . On note Cf sa courbe représentative dans un repère orthogonal du plan,
. On note Cf sa courbe représentative dans un repère orthogonal du plan, 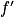 se dérivée et
se dérivée et 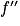 sa dérivée seconde.
sa dérivée seconde.On a tracé ci-dessous la courbe Cf et sa tangente T au point B d'abscisse −1.
On précise que la droite T passe par le point A(0 ; −1).
 |
Partie A : exploitation du graphique.
À l'aide du graphique, répondre aux questions ci-dessous.
1. Préciser f(−1) et 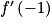 .
.
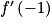 .
.2. La courbe Cf est-elle convexe sur son ensemble de définition ? Justifier.
3. Conjecturer le nombre de solutions de l'équation f(x) = 0 et donner une valeur arrondie à 10−1 près d'une solution.
Partie B : étude de la fonction f
On considère que la fonction f est définie sur ![\left ]-2\, ;\: +\infty \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde34_m5.png) par f(x) = x2 + 2x − 1 + ln(x + 2), où ln désigne la fonction logarithme népérien.
par f(x) = x2 + 2x − 1 + ln(x + 2), où ln désigne la fonction logarithme népérien.
![\left ]-2\, ;\: +\infty \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde34_m5.png) par f(x) = x2 + 2x − 1 + ln(x + 2), où ln désigne la fonction logarithme népérien.
par f(x) = x2 + 2x − 1 + ln(x + 2), où ln désigne la fonction logarithme népérien.1. Déterminer par le calcul la limite de la fonction f en −2. Interpréter graphiquement ce résultat. On admet que 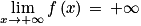 .
.
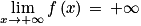 .
.2. Montrer que pour tout x > −2, 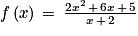 .
.
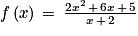 .
.3. Étudier les variations de la fonction f sur ![\left ]-2\, ; +\infty \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde34_m8.png) puis dresser son tableau de variations complet.
puis dresser son tableau de variations complet.
![\left ]-2\, ; +\infty \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde34_m8.png) puis dresser son tableau de variations complet.
puis dresser son tableau de variations complet.4. Montrer que l'équation f(x) = 0 admet une unique solution α sur ![\left ]-2\, ; +\infty \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde34_m9.png) et donner une valeur arrondie de α à 10−2 près.
et donner une valeur arrondie de α à 10−2 près.
![\left ]-2\, ; +\infty \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde34_m9.png) et donner une valeur arrondie de α à 10−2 près.
et donner une valeur arrondie de α à 10−2 près.5. En déduire le signe de f(x) sur ![\left ]-2\, ; +\infty \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde34_m10.png) .
.
![\left ]-2\, ; +\infty \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde34_m10.png) .
.6. Montrer que Cf admet un unique point d'inflexion et déterminer son abscisse.
Partie C : une distance minimale.
Soit g la fonction définie sur ![\left ]-2\, ; +\infty \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde34_m11.png) par g(x) = ln(x + 2).
par g(x) = ln(x + 2).
On note Cg sa courbe représentative dans un repère orthonormé (O; I, J), représenté ci-dessous.
![\left ]-2\, ; +\infty \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde34_m11.png) par g(x) = ln(x + 2).
par g(x) = ln(x + 2).On note Cg sa courbe représentative dans un repère orthonormé (O; I, J), représenté ci-dessous.
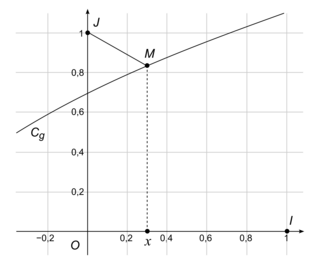 |
Soit M un point de Cg d'abscisse x.
Le but de cette partie est de déterminer pour quelle valeur de x la distance JM est minimale.
On considère la fonction h définie sur![\left ]-2\, ; +\infty \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde34_m12.png) par h(x) = JM2.
par h(x) = JM2.
Le but de cette partie est de déterminer pour quelle valeur de x la distance JM est minimale.
On considère la fonction h définie sur
![\left ]-2\, ; +\infty \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde34_m12.png) par h(x) = JM2.
par h(x) = JM2.1. Justifier que pour tout x > −2, on a : h(x) = x2 + [In(x + 2) − 1]2.
2.
On admet que la fonction h est dérivable sur ![\left ]-2\, ; +\infty \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde34_m13.png) et on note
et on note 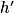 sa fonction dérivée. On admet également que pour tout réel x > −2,
sa fonction dérivée. On admet également que pour tout réel x > −2, 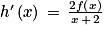 où f est la fonction étudiée en partie B.
où f est la fonction étudiée en partie B.
![\left ]-2\, ; +\infty \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde34_m13.png) et on note
et on note 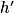 sa fonction dérivée. On admet également que pour tout réel x > −2,
sa fonction dérivée. On admet également que pour tout réel x > −2, 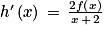 où f est la fonction étudiée en partie B.
où f est la fonction étudiée en partie B. a. Dresser le tableau de variations de h sur ![\left ]-2\, ; +\infty \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde34_m16.png) .
.
Les limites ne sont pas demandées.
![\left ]-2\, ; +\infty \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde34_m16.png) .
.Les limites ne sont pas demandées.
b. En déduire que la valeur de x pour laquelle la distance JM est minimale est α où α est le nombre réel défini à la question 4 de la partie B.
3.
On notera 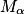 le point de Cg d'abscisse α.
le point de Cg d'abscisse α.
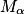 le point de Cg d'abscisse α.
le point de Cg d'abscisse α. a. Montrer que In(α + 2) = 1 − 2α − α−2
b. En déduire que la tangente à Cg au point 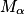 et la droite
et la droite 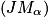 sont perpendiculaires. On pourra utiliser le fait que, dans un repère orthonormé, deux droites sont perpendiculaires lorsque le produit de leurs coefficients directeurs est égal à −1
sont perpendiculaires. On pourra utiliser le fait que, dans un repère orthonormé, deux droites sont perpendiculaires lorsque le produit de leurs coefficients directeurs est égal à −1
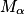 et la droite
et la droite 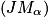 sont perpendiculaires. On pourra utiliser le fait que, dans un repère orthonormé, deux droites sont perpendiculaires lorsque le produit de leurs coefficients directeurs est égal à −1
sont perpendiculaires. On pourra utiliser le fait que, dans un repère orthonormé, deux droites sont perpendiculaires lorsque le produit de leurs coefficients directeurs est égal à −1Annexes
© 2000-2026, Miscellane
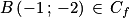 , donc f(−1) = −2.
, donc f(−1) = −2.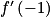 est la pente de la tangente à Cf au point d'abscisse −1, c'est à dire B.
est la pente de la tangente à Cf au point d'abscisse −1, c'est à dire B.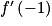 est la pente de T. Or, B et A appartiennent à T donc la pente de T est égale à :
est la pente de T. Or, B et A appartiennent à T donc la pente de T est égale à :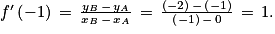
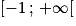 .
.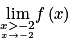
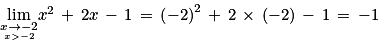
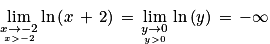
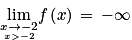
![\left ]-2\, ;\, +\infty \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde34_m29.png) .
.![\left ]-2\, ;\, +\infty \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde34_m30.png) :
: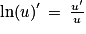
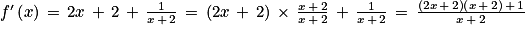
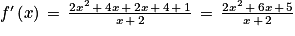
![\left ]-2\, ;\, +\infty \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde34_m34.png) on a 2x2 + 6x + 5 > 0.
on a 2x2 + 6x + 5 > 0.![\left ]-2\, ;\, +\infty \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde34_m35.png) on a x > −2 donc x + 2 > 0.
on a x > −2 donc x + 2 > 0.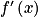 est le quotient de deux nombres strictement positifs.
est le quotient de deux nombres strictement positifs.![\left ]-2\, ;\, +\infty \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde34_m37.png) ,
, 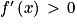 .
.![\left ]-2\, ;\, +\infty \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde34_m39.png) .
.![\left ]-2\, ;\, +\infty \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde34_m40.png) et f est strictement croissante sur
et f est strictement croissante sur ![\left ]-2\, ;\, +\infty \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde34_m41.png) .
.![\left ] \underset{\underset{x> -2}{x\to -2}}{\mathrm{lim}}f\left ( x \right )\, ;\, \displaystyle \lim_{x \to +\infty }f\left ( x \right ) \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde34_m42.png) .
.![\left ]-2\, ;\, +\infty \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde34_m43.png) .
.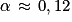 .
.![\left ]-2\, ;\, +\infty \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde34_m45.png) et f s'annule en α.
et f s'annule en α.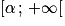 .
.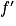 est dérivable sur
est dérivable sur ![\left ]-2\, ;\, +\infty \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde34_m48.png) .
.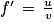
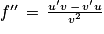
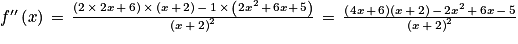

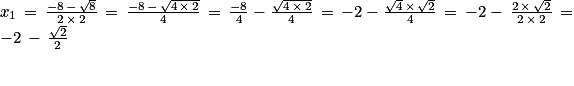
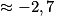
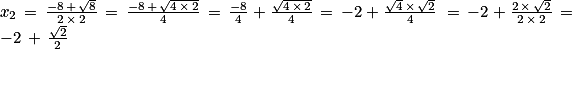
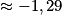
![\left ]-2\, ;\, +\infty \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde34_m57.png) ,
, 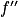 s'annule une unique fois en x2 (car x1 < −2).
s'annule une unique fois en x2 (car x1 < −2).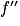 négative sur ]−2 ; x2] et positive sur
négative sur ]−2 ; x2] et positive sur 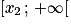 .
.![\left ]-2\, ;\, +\infty \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde34_m61.png) :
: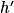 est du signe de f car 2 > 0 et pour tout réel x de
est du signe de f car 2 > 0 et pour tout réel x de ![\left ]-2\, ;\, +\infty \right [](https://static1.assistancescolaire.com/t/images/t_spemat_rde34_m63.png) , x + 2 > 0.
, x + 2 > 0.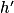 négative sur ]−2 ; α] et
négative sur ]−2 ; α] et 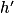 positive sur
positive sur 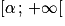 (et
(et 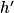 s'annule en α).
s'annule en α).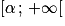 .
.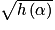 .
.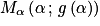 , c'est à dire
, c'est à dire 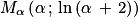 .
.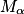 a pour pente
a pour pente 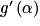 .
.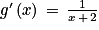 . Donc
. Donc 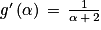 .
.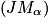 a pour pente :
a pour pente : 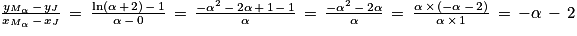 .
.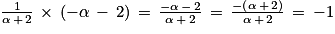 .
.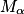 et la droite
et la droite 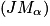 sont perpendiculaires.
sont perpendiculaires.