Équations différentielles, sujet 1. Sujet Bac S, Amérique du Sud, novembre 2007
Énoncé
On souhaite résoudre l'équation différentielle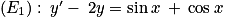 
.
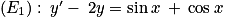.1. Résoudre l'équation différentielle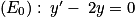 
.
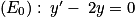.2.
Soient a et b deux réels, et u la fonction définie sur 
par u(x) = a sin x + b cos x. Déterminer a et b pour que u soit solution de l'équation (E1).
par u(x) = a sin x + b cos x. Déterminer a et b pour que u soit solution de l'équation (E1).a. Montrer que v est une solution de l'équation (E0) si et seulement si u + v est solution de (E1).
b. En déduire l'ensemble des solutions de (E1).
3. Déterminer la solution de l'équation (E1) qui s'annule en 0.
La bonne méthode
1. C'est une question de cours.
2. a. On utilise le fait que u est solution de l'équation différentielle.
2. b. La question est classique, on raisonne par équivalence.
2. c. L'équivalence précédente relie la question 2. et la question 1.
3. On connaît la forme des solutions, on trouve la valeur de la constante en appliquant la condition de l'énoncé.
Annexes
, 
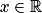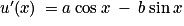. La fonction u est solution de (E1) si et seulement si pour tout 
, 
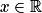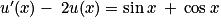, c'est-à-dire (−b − 2a) sin x + (a − 2b)cos x = sin x + cos x. En particulier, pour x = 0, ce qui donne a − 2b = 1 ; pour 
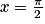, ce qui donne −b − 2a = 1. Il suffit alors de résoudre le système 
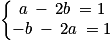. On obtient ainsi 
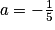et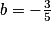 
.
, 
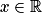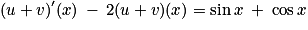, si et seulement si pour tout 
, 
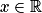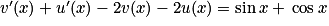, si et seulement si pour tout 
, 
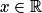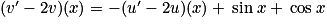. Or u est solution de (E1) donc 
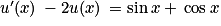. Par conséquent, u + v est solution de (E1) si et seulement si pour tout 
, 
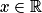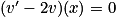ce qui équivaut à v solution de (E0).
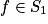si et seulement si 
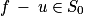. Ainsi, 
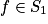si et seulement si, il existe 
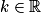, tel que pour tout 
, 
.
.
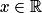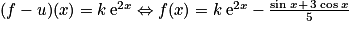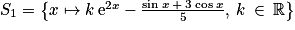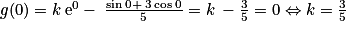. L'unique élément de S1 cherché est donc la fonction g définie sur 
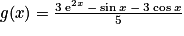.© 2000-2025, Miscellane