Fonction logarithme népérien. D'après sujet Bac S, Centres Étrangers, juin 2008
Énoncé
I. Restitution organisée des connaissances
Prérequis : On rappelle que 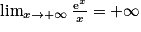 .
.
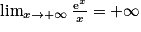 .
.1. Démontrer que 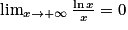 .
.
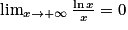 .
.2. En déduire que pour tout entier naturel n non nul, 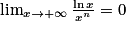 .
.
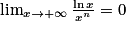 .
.II. Étude d'une fonction f
Soit f la fonction définie sur l'intervalle ![]0\: ;\, +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde12_m4.png) par
par 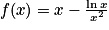 .
.
On note C sa courbe représentative dans un repère orthonormal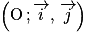 .
.
![]0\: ;\, +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde12_m4.png) par
par 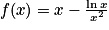 .
.On note C sa courbe représentative dans un repère orthonormal
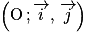 .
.1. Soit u la fonction définie sur l'intervalle ![]0\: ;\, +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde12_m7.png) par u(x) = x3 − 1 + 2 lnx.
par u(x) = x3 − 1 + 2 lnx.
![]0\: ;\, +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde12_m7.png) par u(x) = x3 − 1 + 2 lnx.
par u(x) = x3 − 1 + 2 lnx.a. Étudier le sens de variation de la fonction u sur l'intervalle ![]0\: ;\, +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde12_m8.png) .
.
![]0\: ;\, +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde12_m8.png) .
.b. Calculer u(1) et en déduire le signe de u(x) pour x appartenant à l'intervalle ![]0\: ;\, +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde12_m9.png) .
.
![]0\: ;\, +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde12_m9.png) .
.2. Étude de la fonction f.
a. Déterminer les limites de f en 0 et en 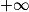 .
.
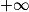 .
.b. Déterminer la fonction dérivée de f.
3. Éléments graphiques.
a. Démontrer que la droite (Δ) d'équation y = x est asymptote oblique à la courbe C.
b. Déterminer la position de C par rapport à la droite (Δ).
La bonne méthode
Partie I. 1. Privilégier la composition des limites.
Partie I. 2. Faire apparaître des limites connues sans faire apparaître une forme indéterminée.
Partie II. 1. a. On dérive la fonction et on examine le signe de ce que l'on vient d'obtenir avant toute manipulation algébrique.
Partie II. 1. b. On utilise la stricte monotonie de la fonction.
Partie II. 2. a. Lorsque l'on cherche des limites, on commence par regarder si les théorèmes généraux sur les opérations répondent. Si ce n'est pas le cas, si la forme est indéterminée, on transforme les écritures pour lever les indéterminations, en particulier en invoquant les croissances comparées des fonctions en jeu.
Partie II. 2. b. On dérive la fonction et on relit la partie II. 1.
Partie II. 3. a. En général, pour montrer que la droite d'équation y = ax + b est asymptote à une courbe, on effectue la différence f(x) −(ax + b) et on montre que cette différence tend vers 0.
Partie II. 3. b. On étudie le signe de l'expression f(x) −(ax + b).
Partie I. 2. Faire apparaître des limites connues sans faire apparaître une forme indéterminée.
Partie II. 1. a. On dérive la fonction et on examine le signe de ce que l'on vient d'obtenir avant toute manipulation algébrique.
Partie II. 1. b. On utilise la stricte monotonie de la fonction.
Partie II. 2. a. Lorsque l'on cherche des limites, on commence par regarder si les théorèmes généraux sur les opérations répondent. Si ce n'est pas le cas, si la forme est indéterminée, on transforme les écritures pour lever les indéterminations, en particulier en invoquant les croissances comparées des fonctions en jeu.
Partie II. 2. b. On dérive la fonction et on relit la partie II. 1.
Partie II. 3. a. En général, pour montrer que la droite d'équation y = ax + b est asymptote à une courbe, on effectue la différence f(x) −(ax + b) et on montre que cette différence tend vers 0.
Partie II. 3. b. On étudie le signe de l'expression f(x) −(ax + b).
Annexes
© 2000-2026, Miscellane
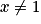 (ce qui est le cas au voisinage de
(ce qui est le cas au voisinage de 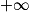 ), on a :
), on a :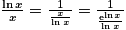 . Or
. Or 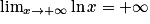 , donc
, donc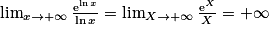 . Par composition avec la fonction inverse, on obtient donc que
. Par composition avec la fonction inverse, on obtient donc que 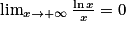 .
. 2, on a
2, on a 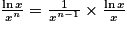 . Comme
. Comme 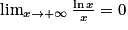 et
et 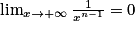 , on a bien, par produit de limites, le résultat demandé.
, on a bien, par produit de limites, le résultat demandé.![]0\, ;\, +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde12_m20.png) , et pour tout x > 0,
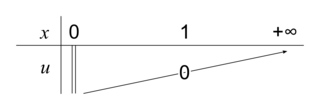
, et pour tout x > 0, 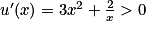 comme somme de deux quantités strictement positives. On en déduit que u est strictement croissante sur
comme somme de deux quantités strictement positives. On en déduit que u est strictement croissante sur ![]0\, ;\, +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde12_m22.png) .
.
![]1\, ;\, +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde12_m23.png) .
.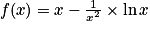 .
.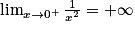 ,
, 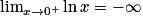 . Donc
. Donc 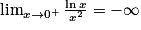 . On en déduit que
. On en déduit que 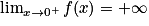 . (La droite d'équation x = 0 est asymptote à la courbe représentative de la fonction f.)
. (La droite d'équation x = 0 est asymptote à la courbe représentative de la fonction f.)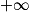 , la partie I nous permet d'affirmer que
, la partie I nous permet d'affirmer que 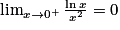 . On en déduit que
. On en déduit que 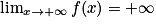 .
.![]0\, ;\, +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde12_m32.png) , et pour tout x > 0, on a :
, et pour tout x > 0, on a :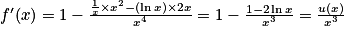 . Le signe de
. Le signe de 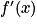 sur
sur ![]0\, ;\, +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde12_m35.png) est clairement celui de u(x).
est clairement celui de u(x). 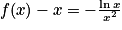 . On a vu que
. On a vu que 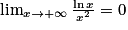 , donc
, donc 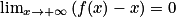 , ce qui suffit pour prouver que la droite d'équation y = x est asymptote oblique à la courbe représentative de f au voisinage de
, ce qui suffit pour prouver que la droite d'équation y = x est asymptote oblique à la courbe représentative de f au voisinage de 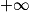 .
.![]0\, ;\, +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde12_m40.png) , le signe de f(x) − x est l'opposé de celui de
, le signe de f(x) − x est l'opposé de celui de 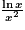 , donc l'opposé de celui de lnx. On en déduit que la courbe représentative de f coupe son asymptote au point de coordonnées (1 ; 1) et est située :
, donc l'opposé de celui de lnx. On en déduit que la courbe représentative de f coupe son asymptote au point de coordonnées (1 ; 1) et est située :![]1\, ;\, +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde12_m42.png) .
.