Continuité des fonctions d'une variable réelle
Énoncé
Partie A
On considère la fonction C définie sur l'intervalle [5 ; 60] par :
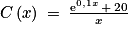
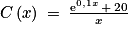
1. On désigne par 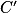 la dérivée de la fonction C.
la dérivée de la fonction C.
Montrer que pour tout![x\: \in \left [ 5\, ;\, 60 \right ]](https://static1.assistancescolaire.com/t/images/t_spemat_rde11_m3.png) ,
, 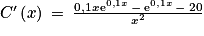 .
.
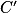 la dérivée de la fonction C.
la dérivée de la fonction C.Montrer que pour tout
![x\: \in \left [ 5\, ;\, 60 \right ]](https://static1.assistancescolaire.com/t/images/t_spemat_rde11_m3.png) ,
, 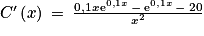 .
.2.
On considère la fonction f définie sur [5 ; 60] par :
f(x) = 0,1x0,1x − e0,1x − 20
f(x) = 0,1x0,1x − e0,1x − 20
a. Montrer que la fonction f est strictement croissante sur [5 ; 60].
b. Monter que l'équation f(x) = 0 admet une unique solution α dans [5 ; 60].
c. Donner un encadrement à l'unité de α.
d. En déduire le tableau de signes de f(x) sur [5 ; 60].
3. En déduire le tableau de variations de C sur [5 ; 60].
4.
En utilisant la question précédente, déterminer le nombre de solutions des équations suivantes :
a. C(x) = 2.
b. C(x) = 5.
Partie B
Une entreprise fabrique chaque mois x vélos de course, avec ![x\: \in \left [ 5\, ;\, 60 \right ]](https://static1.assistancescolaire.com/t/images/t_spemat_rde11_m5.png) .
.
Le coût moyen de fabrication, exprimé en milliers d'euros, pour une production de x vélos de course, est donné par la fonction C définie dans la partie A.
Déterminer le nombre de vélos à produire pour que le coût de fabrication moyen soit minimal.
![x\: \in \left [ 5\, ;\, 60 \right ]](https://static1.assistancescolaire.com/t/images/t_spemat_rde11_m5.png) .
.Le coût moyen de fabrication, exprimé en milliers d'euros, pour une production de x vélos de course, est donné par la fonction C définie dans la partie A.
Déterminer le nombre de vélos à produire pour que le coût de fabrication moyen soit minimal.
La bonne méthode un+1 = f(un).
PARTIE A
1. Utiliser la dérivée d'un quotient de deux fonctions.
2.
a. Dériver la fonction f et étudier son signe.
b. Utiliser le théorème des valeurs intermédiaires.
c. Utiliser la calculatrice.
d. Faire le tableau de signes de f(x) sur [5 ; 60].
3. Remarquer que 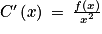 .
.
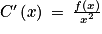 .
.4.
a. et b. Utiliser le théorème des valeurs intermédiaires.
PARTIE B
Utiliser les résultats de la partie A.Penser à rédiger une conclusion.
Annexes
© 2000-2026, Miscellane
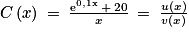 avec u(x) = e0,1x + 20 et v(x) = x. On a
avec u(x) = e0,1x + 20 et v(x) = x. On a 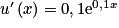 ,
, 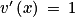 et
et 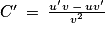 .
.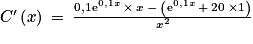
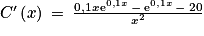
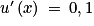 ,
, 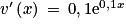 et
et 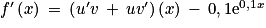 .
.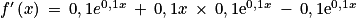
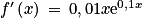
![x\: \in \left [ 5\, ;\, 60 \right ]](https://static1.assistancescolaire.com/t/images/t_spemat_rde11_m18.png) , 0,01x > 0 et e0,1x > 0. Donc
, 0,01x > 0 et e0,1x > 0. Donc 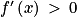 sur [5 ; 60]. Et la fonction f est strictement croissante sur [5 ; 60].
sur [5 ; 60]. Et la fonction f est strictement croissante sur [5 ; 60].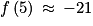 et
et 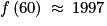 . Donc f(5) < 0 < f(60)
. Donc f(5) < 0 < f(60)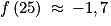 et
et 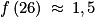 . Donc 25 < α < 26.
. Donc 25 < α < 26.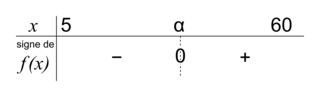
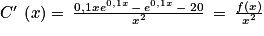 . Donc
. Donc 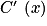 est du signe de f(x).
est du signe de f(x).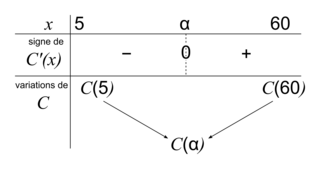
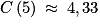 ,
, 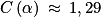 et
et 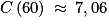 .
.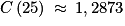 et
et 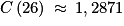 . Donc le coût moyen minimal sera atteint pour une production de 26 vélos.
. Donc le coût moyen minimal sera atteint pour une production de 26 vélos.