Suites, sujet 1. Suites récurrentes d'ordre 1. D'après sujet Bac S, Amérique du Sud, novembre 1994
Énoncé
On considère la suite 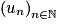 à termes positifs, telle que u0 = 5 et vérifiant pour tout entier naturel
à termes positifs, telle que u0 = 5 et vérifiant pour tout entier naturel 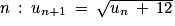 .
.
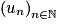 à termes positifs, telle que u0 = 5 et vérifiant pour tout entier naturel
à termes positifs, telle que u0 = 5 et vérifiant pour tout entier naturel 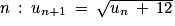 .
.1. Montrer que, pour tout entier naturel n, 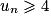 .
.
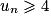 .
.2. On se propose, dans cette question, d'étudier de deux manières la convergence de cette suite.
Méthode 1.
a) Démontrer que la suite est décroissante.
b) Déduire de ce qui précède que la suite est convergente, puis trouver sa limite.
Méthode 2.
a. Montrer que pour tout 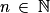 ,
, 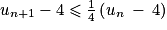 .
.
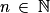 ,
, 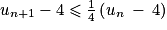 .
.b. Montrer que pour tout 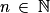 ,
, 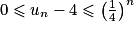 .
.
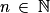 ,
, 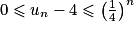 .
.c. En déduire que 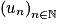 converge et donner sa limite.
converge et donner sa limite.
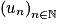 converge et donner sa limite.
converge et donner sa limite.La bonne méthode
1. On peut procéder par récurrence en utilisant le sens de variation de la fonction 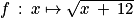 .
.
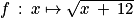 .
.2.
Méthode 1.
a. Il y a de nombreuses façons de résoudre cette question. On peut procéder par récurrence ou évaluer le signe de 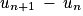 , par exemple.
, par exemple.
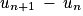 , par exemple.
, par exemple.b. La suite est décroissante et minorée. S'agissant de la limite l, il va s'agir de justifier qu'elle est solution de l'équation 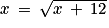 , et qu'elle est supérieure ou égale à 4.
, et qu'elle est supérieure ou égale à 4.
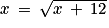 , et qu'elle est supérieure ou égale à 4.
, et qu'elle est supérieure ou égale à 4.Méthode 2.
a. On va utiliser la méthode dite de la quantité conjuguée
b. On va procéder par récurrence.
c. On doit penser au théorème des gendarmes.
Annexes
© 2000-2026, Miscellane
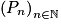 la suite de propositions de terme général :
la suite de propositions de terme général : 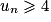 .
.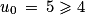 Donc la proposition est vraie au rang 0.
Donc la proposition est vraie au rang 0.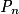 est vraie. On a
est vraie. On a 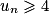 . Or la fonction
. Or la fonction 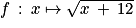 est croissante sur
est croissante sur 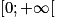 . Donc
. Donc 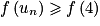 c'est-à-dire
c'est-à-dire 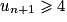 . Donc
. Donc 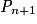 est vraie et la proposition est héréditaire.
est vraie et la proposition est héréditaire.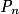 est vraie pour tout entier naturel n donc
est vraie pour tout entier naturel n donc 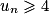 pour tout
pour tout 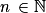 .
.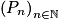 la suite de propositions de terme général :
la suite de propositions de terme général : 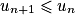 .
.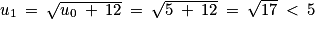 . Donc
. Donc 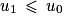 et la proposition est vraie au rang 0.
et la proposition est vraie au rang 0.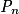 est vraie. On a
est vraie. On a 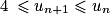 . Or la fonction f est croissante sur
. Or la fonction f est croissante sur 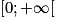 . Donc
. Donc 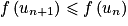 , c'est-à-dire
, c'est-à-dire 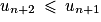 . Donc
. Donc 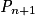 est vraie et la proposition est héréditaire.
est vraie et la proposition est héréditaire.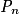 est vraie pour tout entier naturel n, donc
est vraie pour tout entier naturel n, donc 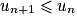 pour tout
pour tout 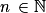 . La suite est donc bien décroissante.
. La suite est donc bien décroissante.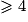 . Par définition de la convergence, on a
. Par définition de la convergence, on a 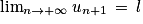 , donc
, donc 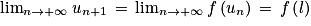 puisque la fonction f est continue sur
puisque la fonction f est continue sur 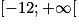 , donc en particulier en
, donc en particulier en 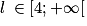 .
.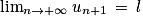 et f(l) = l On va donc résoudre l'équation
et f(l) = l On va donc résoudre l'équation 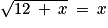 , qui n'a de sens que pour
, qui n'a de sens que pour 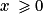 .
.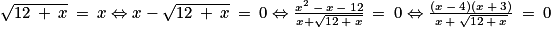 .
.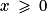 . Donc l'unique solution est x = –4 et on a
. Donc l'unique solution est x = –4 et on a 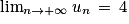 .
.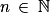 :
: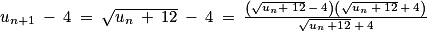 .
.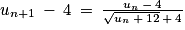 .
.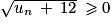 donc
donc 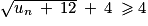 et
et 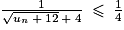 . En multipliant chaque terme de l'inégalité par
. En multipliant chaque terme de l'inégalité par 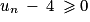 , on obtient
, on obtient 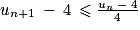 .
.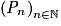 la suite de propositions de terme général :
la suite de propositions de terme général : 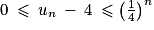 .
.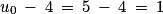 et
et 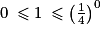 . Donc la proposition est vraie au rang 0.
. Donc la proposition est vraie au rang 0.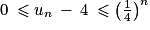 . D'où
. D'où 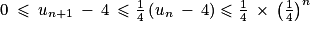 , soit
, soit 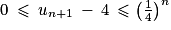 . Donc
. Donc 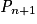 est vraie et la proposition est héréditaire.
est vraie et la proposition est héréditaire.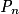 est vraie pour tout entier naturel n, donc
est vraie pour tout entier naturel n, donc 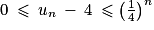 pour tout
pour tout 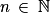 .
. , alors
, alors 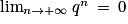 . On a ainsi
. On a ainsi 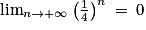 , ce qui entraîne grâce au théorème des gendarmes que
, ce qui entraîne grâce au théorème des gendarmes que 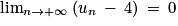 . En d'autres termes,
. En d'autres termes, 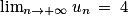 .
.