Représentations paramétriques et équations cartésiennes. D'après sujet Bac S, Pondichéry, mai 2018
Énoncé
Dans l'espace muni du repère orthonormé 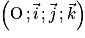 d'unité 1 cm, on considère les points A, B, C et D de coordonnées respectives (2 ; 1 ; 4), (4 ; –1 ; 0), (0 ; 3 ; 2) et (4 ; 3 ; –2).
d'unité 1 cm, on considère les points A, B, C et D de coordonnées respectives (2 ; 1 ; 4), (4 ; –1 ; 0), (0 ; 3 ; 2) et (4 ; 3 ; –2).
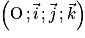 d'unité 1 cm, on considère les points A, B, C et D de coordonnées respectives (2 ; 1 ; 4), (4 ; –1 ; 0), (0 ; 3 ; 2) et (4 ; 3 ; –2).
d'unité 1 cm, on considère les points A, B, C et D de coordonnées respectives (2 ; 1 ; 4), (4 ; –1 ; 0), (0 ; 3 ; 2) et (4 ; 3 ; –2).1. Les points A, B, C et D sont-ils coplanaires ?
2. Déterminer une représentation paramétrique de la droite (CD).
3.
Soit M un point de la droite (CD).
a. Déterminer les coordonnées du point M tel que la distance BM soit minimale.
b. On note H le point de la droite (CD) ayant pour coordonnées (3 ; 3 ; –1) Vérifier que les droites (CD) et (BH) sont perpendiculaires.
c. Montrer que l'aire du triangle BCD est égale à 12 cm2.
4.
a. Démontrer que le vecteur 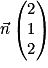 est un vecteur normal au plan (BCD).
est un vecteur normal au plan (BCD).
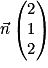 est un vecteur normal au plan (BCD).
est un vecteur normal au plan (BCD).b. Déterminer une équation cartésienne du plan (BCD).
c. Déterminer une représentation paramétrique de la droite (Δ) passant par A et orthogonale au plan (BCD).
d. Démontrer que le point I, intersection de la droite Δ et du plan (BCD) a pour coordonnées 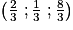
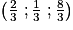
5. Calculer le volume du tétraèdre ABCD.
La bonne méthode
1. Autrement dit les vecteurs 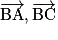 et
et 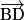 sont-ils coplanaires ?
sont-ils coplanaires ?
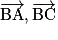 et
et 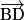 sont-ils coplanaires ?
sont-ils coplanaires ?2. (CD) est l'ensemble des points M(x ; y ; z) alignés avec C et D.
3.
a. La question précédente permet de caractériser les points de (CD) en fonction d'un paramètre t, on calcule BM2 en fonction de t, et on détermine la valeur de t qui minimise la fonction.
3.
b. Le produit scalaire est le bon outil.
3.
c. Ce qui précède permet d'affirmer que [BH] est la hauteur du triangle BCD issue de B.
4.
a. Une droite est orthogonale à un plan si et seulement si elle est orthogonale à deux droites sécantes de ce plan.
4.
b. Si une droite est orthogonale à un plan alors elle est orthogonale à toutes les droites de ce plan.
4.
c. On connaît un point de la droite et un vecteur directeur.
4.
d. Le point d'intersection est élément de (Δ) ce qui contraint ses coordonnées. Et celles-ci vérifient aussi une équation cartésienne de (BCD).
5. Le volume d'un tétraèdre est 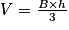 où B désigne la surface de la base et h la hauteur du solide.
où B désigne la surface de la base et h la hauteur du solide.
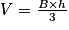 où B désigne la surface de la base et h la hauteur du solide.
où B désigne la surface de la base et h la hauteur du solide.Annexes
© 2000-2026, Miscellane
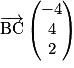 et
et 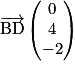 Ils ne sont pas colinéaires, donc les points B, C et D ne sont pas alignés : ils déterminent un plan unique (BCD) dont un repère est
Ils ne sont pas colinéaires, donc les points B, C et D ne sont pas alignés : ils déterminent un plan unique (BCD) dont un repère est 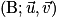 où
où 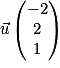 et
et 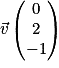 Les quatre points A, B, C et D sont coplanaires si et seulement si
Les quatre points A, B, C et D sont coplanaires si et seulement si 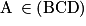 soit si et seulement si il existe un unique couple de réels (a ; b) tel que
soit si et seulement si il existe un unique couple de réels (a ; b) tel que 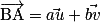 en d'autres termes, si et seulement si le système
en d'autres termes, si et seulement si le système 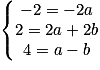 d'inconnues a et b admet une unique solution. De façon évidente, ce système est équivalent à
d'inconnues a et b admet une unique solution. De façon évidente, ce système est équivalent à 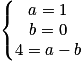 qui n'admet aucune solution. Les points A, B, C et D ne sont dont pas coplanaires. Les vecteurs
qui n'admet aucune solution. Les points A, B, C et D ne sont dont pas coplanaires. Les vecteurs 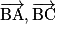 et
et 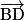 forment une base de l'espace des vecteurs et ABCD est un tétraèdre.
forment une base de l'espace des vecteurs et ABCD est un tétraèdre.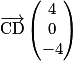 par exemple
par exemple 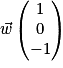 Un point M(x ; y ; z) appartient à la droite (CD) si et seulement si
Un point M(x ; y ; z) appartient à la droite (CD) si et seulement si 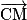 et
et 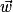 sont colinéaires, soit si et seulement si il existe un réel t tel que
sont colinéaires, soit si et seulement si il existe un réel t tel que 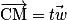 L'écriture sous forme d'un système de cette équivalence donne un système d'équations paramétriques de (CD).
L'écriture sous forme d'un système de cette équivalence donne un système d'équations paramétriques de (CD).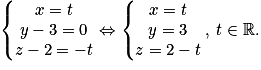
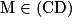 il existe
il existe 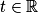 tel que M ait pour coordonnées (t ; 3 ; 2 – t)
tel que M ait pour coordonnées (t ; 3 ; 2 – t)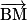 a pour coordonnées
a pour coordonnées 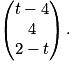
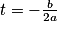 Ici, BM est donc minimale pour t = 3 soit au point de coordonnées (3 ; 3 ; –1) Cette distance minimale vaut
Ici, BM est donc minimale pour t = 3 soit au point de coordonnées (3 ; 3 ; –1) Cette distance minimale vaut 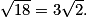
 a pour coordonnées
a pour coordonnées 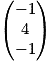 On sait que
On sait que 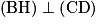 si et seulement si
si et seulement si 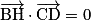 . Or
. Or 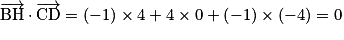 . Les droites (BH) et (CD) sont orthogonales et même perpendiculaires puisqu'elles se coupent en H.
. Les droites (BH) et (CD) sont orthogonales et même perpendiculaires puisqu'elles se coupent en H.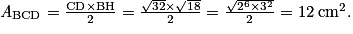
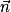 est normal au plan (BCD) dont un repère est
est normal au plan (BCD) dont un repère est 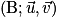 si et seulement si
si et seulement si 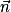 est orthogonal à la fois à
est orthogonal à la fois à 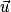 et à
et à 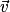 . Or
. Or 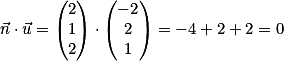 et
et 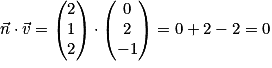 . On a donc
. On a donc 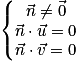 , donc
, donc 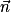 est normal au plan (BCD).
est normal au plan (BCD).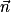 .
.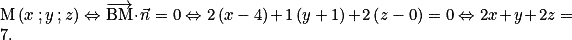
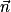 et passe par A. Un système d'équations paramétriques de cette droite est donc :
et passe par A. Un système d'équations paramétriques de cette droite est donc :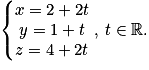
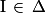 donc il existe un unique
donc il existe un unique 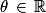 tel que
tel que 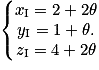
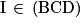 donc 2xI + yI + 2zI = 7.
donc 2xI + yI + 2zI = 7.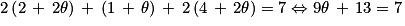 . Donc
. Donc 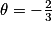 On en déduit que
On en déduit que 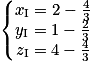 et donc I a pour coordonnées
et donc I a pour coordonnées 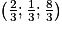 .
.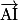 a pour coordonnées
a pour coordonnées 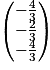 . On en déduit que
. On en déduit que 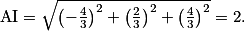
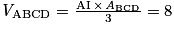 . Le volume du tétraèdre est 8 cm3
. Le volume du tétraèdre est 8 cm3