Orthogonalité et distances dans l'espace, sujet 2
Énoncé
On munit l'espace du repère orthonormé 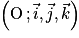 .
.
Soit la pyramide régulière ABCDS à base carrée telle que :
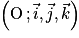 .
.Soit la pyramide régulière ABCDS à base carrée telle que :
• O centre de la base ABCD ;
• A(–1 ; –1 ; 0), B(1 ; –1 ; 0), C(1 ; 1 ; 0), D(–1 ; 1 ; 0) ;
• 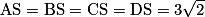 .
.
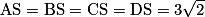 .
.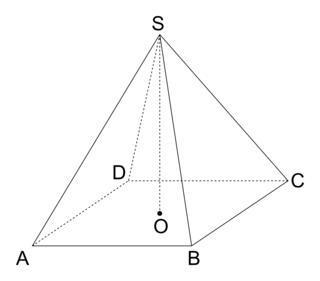 |
1.
a. Calculer AC.
b. Calculer le produit scalaire 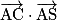 de deux manières différentes pour en déduire l'angle
de deux manières différentes pour en déduire l'angle 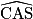 arrondi au degré près.
arrondi au degré près.
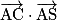 de deux manières différentes pour en déduire l'angle
de deux manières différentes pour en déduire l'angle 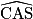 arrondi au degré près.
arrondi au degré près.2.
On admet que S(0 ; 0 ; 4) Soient M, N, P et Q tels que :
• M milieu de l'arête [SC] ;
• N milieu de l'arête [SA] ;
• P vérifiant 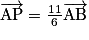 ;
;
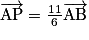 ;
;• Q vérifiant 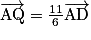 .
.
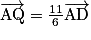 .
.a. Calculer les coordonnées des points M, N, P et Q.
b. Calculer 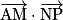 et
et 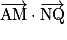
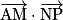 et
et 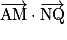
c. En déduire les positions relatives de la droite (AM) et du plan (NPQ).
La bonne méthode
1.
a. Utiliser la formule de la distance entre deux points dans un repère orthonormé de l'espace.
b. Calculer le produit scalaire en utilisant la formule de polarisation 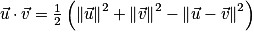 et la définition du produit scalaire
et la définition du produit scalaire 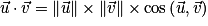 .
.
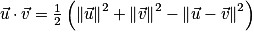 et la définition du produit scalaire
et la définition du produit scalaire 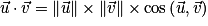 .
.2.
a. Utiliser la formule des coordonnées d'un milieu pour les points M et N. Utiliser l'égalité vectorielle pour les points P et Q.
b. Calculer le produit scalaire en utilisant les coordonnées.
c. Déduire des questions précédentes l'orthogonalité de vecteurs.
Annexes
© 2000-2026, Miscellane
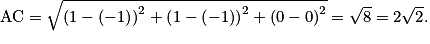
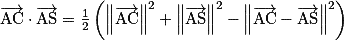
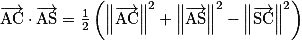
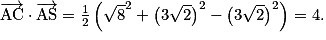
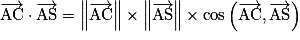
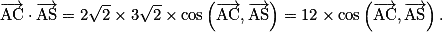
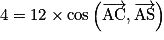 et
et 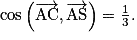
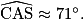
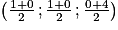 soit
soit 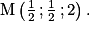
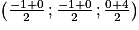 soit
soit 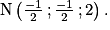
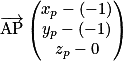 et
et 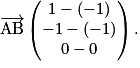 Or
Or 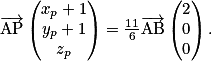
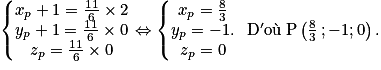
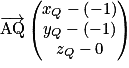 et
et 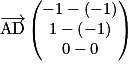 . Or
. Or 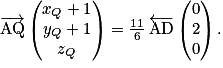
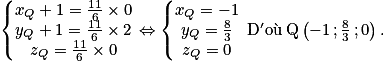
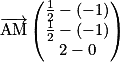 , soit
, soit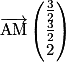 . On a
. On a 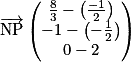 , soit
, soit 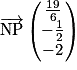 .
.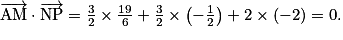
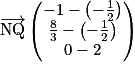 , soit
, soit 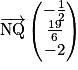 .
.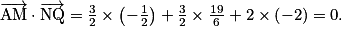
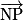 et
et 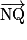 comme vecteurs directeurs. Or
comme vecteurs directeurs. Or 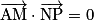 et
et  , donc
, donc 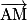 est un vecteur normal au plan (NPQ).
est un vecteur normal au plan (NPQ).