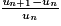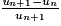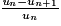La population est en évolution constante. Afin d'ajuster les ressources, il est important de prédire la démographie, c'est-à-dire la dynamique des populations, et la manière dont vont évoluer les moyens qui leur seront nécessaires. Pour prédire l'évolution d'un système, les scientifiques utilisent des modèles mathématiques. Thomas Malthus, économiste anglais du xixe siècle, est connu pour cette approche mathématique dans le cadre de son étude de l'évolution de la population.
Thomas Malthus publie son Essai sur le principe de population en 1798. Il y pointe le déséquilibre entre la croissance de la population et celle des subsistances. Selon Malthus, la population augmente toujours plus vite que la production des ressources nécessaires. Pour résoudre ce problème, il propose de réduire la croissance démographique ou d'augmenter la quantité de vivres, afin de faire correspondre la population à la quantité de denrées alimentaires. Sa théorie a déclenché de nombreuses polémiques. Si les prédictions du modèle sont correctes sur un temps court, elles sont irréalistes sur un temps plus long, notamment en raison de l'insuffisance des ressources disponibles.
D'autres modèles voient ensuite le jour, mais tous ont des limites. Actuellement, des modèles plus élaborés prévoient que nous serons environ 10 milliards d'êtres humains en 2050.
Thomas Malthus publie son Essai sur le principe de population en 1798. Il y pointe le déséquilibre entre la croissance de la population et celle des subsistances. Selon Malthus, la population augmente toujours plus vite que la production des ressources nécessaires. Pour résoudre ce problème, il propose de réduire la croissance démographique ou d'augmenter la quantité de vivres, afin de faire correspondre la population à la quantité de denrées alimentaires. Sa théorie a déclenché de nombreuses polémiques. Si les prédictions du modèle sont correctes sur un temps court, elles sont irréalistes sur un temps plus long, notamment en raison de l'insuffisance des ressources disponibles.
D'autres modèles voient ensuite le jour, mais tous ont des limites. Actuellement, des modèles plus élaborés prévoient que nous serons environ 10 milliards d'êtres humains en 2050.
Variation absolue, variation relative
Soit une population dont l'effectif évolue par palier, de la valeur un à la période n à l'effectif un+1 à la période n + 1. On appelle :
• variation absolue, la différence un+1 − un ;
• variation relative ou taux d'accroissement (ou de variation) entre les états un et un+1, le rapport 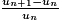 .
.
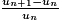 .
.Les suites
Par définition, une suite est une fonction u définie sur l'ensemble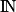 des entiers naturels. À chaque entier naturel n, on associe son image u (n) que l'on note aussi un. L'ensemble des nombres un forme une suite.
des entiers naturels. À chaque entier naturel n, on associe son image u (n) que l'on note aussi un. L'ensemble des nombres un forme une suite.On dit que un est le terme de rang (ou d'indice) n de la suite (u).
La suite arithmétique et le modèle linéaire
Un modèle mathématique simple est le modèle linéaire. Lorsque, pour tout entier naturel n, la variation absolue entre deux états consécutifs est constante, c'est-à-dire un+1 − un = cste, on dit que la suite est arithmétique. La constante obtenue est appelée raison de la suite arithmétique et sera notée r. On peut ainsi écrire :un+1 − un = r
Si u0 est le premier terme de la suite arithmétique, alors :
un = u0 + n × r
Les points de coordonnées (n ; un) sont situés sur une droite. Dans la réalité, pour une population dont la variation absolue est presque constante d'un palier à l'autre, on peut ajuster le nuage de points qui la représente par une droite. Le modèle linéaire est inadapté pour représenter l'évolution d'une grandeur dont la variation absolue change fortement d'un palier à l'autre. Il ne permet pas non plus de représenter l'évolution d'une population humaine ou animale. En revanche, l'évolution d'une ressource est souvent bien modélisée par le modèle linéaire.
La suite géométrique et le modèle exponentiel
On considère que tous les termes de la suite sont non nuls. Lorsque pour tout entier naturel n, le rapport entre deux états consécutifs est constant, c'est-à-dire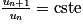 , on dit que la suite est géométrique. La constante obtenue est appelée raison de la suite géométrique et sera notée q. On peut ainsi écrire :
, on dit que la suite est géométrique. La constante obtenue est appelée raison de la suite géométrique et sera notée q. On peut ainsi écrire :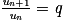
Si u0 est le premier terme de la suite géométrique, alors :
un = u0 × qn
Une grandeur discrète u varie de manière exponentielle en fonction du palier entier n si sa variation absolue un+1 − un est proportionnelle à sa valeur courante un.
Dans ce cas, sa variation relative (ou taux de variation) est constante, et la suite de terme général un est géométrique, c'est-à-dire que un+1 − un = k × un, où k est une constante réelle.
Dans la réalité, pour une population dont le taux de variation est presque constant d'un palier à l'autre, on peut ajuster le nuage de points par un modèle exponentiel.
Le modèle démographique : application du modèle de Malthus
Chaque modèle démographique doit être mis en œuvre à partir de trois étapes. Il faut :
• identifier le type de modèle le mieux adapté pour traduire la réalité (linéaire, exponentiel.) ;
• déterminer les paramètres du modèle (le premier terme, la raison…) ;
• comparer le modèle et les observations, et donner éventuellement un domaine de validité du modèle. Parfois, le modèle n'est concordant avec les observations que sur un petit domaine, il faut alors le préciser.
Le modèle démographique de Malthus est un modèle exponentiel d'évolution de l'effectif de la population. Il prévoit que l'effectif de la population décroît vers 0 si le taux de mortalité est supérieur au taux de natalité, et croît vers l'infini si le taux de natalité? est supérieur au taux de mortalité.
« Selon la table d'Euler, si l'on se base sur une mortalité de 1 sur 36 et si naissances et morts sont dans le rapport de 3 à 1, le chiffre de la population doublera en 12 années et 4/5. Ce n'est point là une simple supposition : c'est une réalité qui s'est produite plusieurs fois, et à de courts intervalles. Cependant, pour ne pas être taxés d'exagération, nous nous baserons sur l'accroissement le moins rapide, qui est garanti par la concordance de tous les témoignages. Nous pouvons être certains que lorsque la population n'est arrêtée par aucun obstacle, elle double tous les vingt-cinq ans, et croît ainsi de période en période selon une progression géométrique. Il est moins facile de mesurer l'accroissement des produits de la Terre. » (Extrait de Malthus, Essais sur le principe de population, 1798.)
La première année, en supposant pour simplifier que la population soit de 360 personnes, le nombre de morts est égal à :
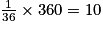 morts
morts
Le nombre de naissance est donc :
10 ×3 = 30 naissances
À la fin de la première année, la population sera donc de :
360 − 10 + 30 = 380 habitants.
Avec le même raisonnement que précédemment, on obtient le tableau de résultats suivants (en arrondissant les résultats à l'unité). (Attention : conserver la valeur exacte du nombre de morts pour effectuer les calculs du nombre de naissances et de la population en fin d'année) :
Le doublement de la population se fait donc entre la 12e et la 13e année. La 12e année, il y a 689 habitants. Comme il y a 365 jours par an (les années non bissextiles) et que 365 a pour diviseur 5, faisons le même raisonnement que précédemment, mais par tranche de 1/5.
Pour le premier 1/5 de l'année, le nombre de morts est :
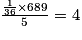 morts
morts
Le nombre de naissances est toujours trois fois supérieur au nombre de morts. On obtient ainsi le tableau suivant (en arrondissant les résultats à l'unité) :
Au bout de la 4e tranche, c'est-à-dire au bout de 12 ans et 4/5, on a un doublement de la population. Le calcul du rapport un+1/un donne :
Les rapports sont égaux. La modélisation peut être effectuée par une suite géométrique de premier terme 360 et de raison 1,06.
« Selon la table d'Euler, si l'on se base sur une mortalité de 1 sur 36 et si naissances et morts sont dans le rapport de 3 à 1, le chiffre de la population doublera en 12 années et 4/5. Ce n'est point là une simple supposition : c'est une réalité qui s'est produite plusieurs fois, et à de courts intervalles. Cependant, pour ne pas être taxés d'exagération, nous nous baserons sur l'accroissement le moins rapide, qui est garanti par la concordance de tous les témoignages. Nous pouvons être certains que lorsque la population n'est arrêtée par aucun obstacle, elle double tous les vingt-cinq ans, et croît ainsi de période en période selon une progression géométrique. Il est moins facile de mesurer l'accroissement des produits de la Terre. » (Extrait de Malthus, Essais sur le principe de population, 1798.)
La première année, en supposant pour simplifier que la population soit de 360 personnes, le nombre de morts est égal à :
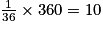 morts
mortsLe nombre de naissance est donc :
10 ×3 = 30 naissances
À la fin de la première année, la population sera donc de :
360 − 10 + 30 = 380 habitants.
Avec le même raisonnement que précédemment, on obtient le tableau de résultats suivants (en arrondissant les résultats à l'unité). (Attention : conserver la valeur exacte du nombre de morts pour effectuer les calculs du nombre de naissances et de la population en fin d'année) :
| Année | Population en début d'année | Nombre de morts | Nombre de naissances | Population en fin d'année |
|---|---|---|---|---|
| 1 | 360 | 10 | 30 | 380 |
| 2 | 380 | 11 | 32 | 401 |
| 3 | 401 | 11 | 33 | 423 |
| 4 | 423 | 12 | 35 | 447 |
| 5 | 447 | 12 | 37 | 472 |
| 6 | 472 | 13 | 39 | 498 |
| 7 | 498 | 14 | 42 | 526 |
| 8 | 526 | 15 | 44 | 555 |
| 9 | 555 | 15 | 46 | 586 |
| 10 | 586 | 16 | 49 | 619 |
| 11 | 619 | 17 | 52 | 653 |
| 12 | 653 | 18 | 54 | 689 |
| 13 | 689 | 19 | 57 | 727 |
Le doublement de la population se fait donc entre la 12e et la 13e année. La 12e année, il y a 689 habitants. Comme il y a 365 jours par an (les années non bissextiles) et que 365 a pour diviseur 5, faisons le même raisonnement que précédemment, mais par tranche de 1/5.
Pour le premier 1/5 de l'année, le nombre de morts est :
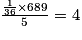 morts
mortsLe nombre de naissances est toujours trois fois supérieur au nombre de morts. On obtient ainsi le tableau suivant (en arrondissant les résultats à l'unité) :
| Tranche | Population en début de mois | Nombre de morts | Nombre de naissances | Population en fin de mois |
|---|---|---|---|---|
| 1re tranche | 689 | 4 | 11 | 697 |
| 2e tranche | 697 | 4 | 12 | 705 |
| 3e tranche | 705 | 4 | 12 | 713 |
| 4e tranche | 713 | 4 | 12 | 721 |
Au bout de la 4e tranche, c'est-à-dire au bout de 12 ans et 4/5, on a un doublement de la population. Le calcul du rapport un+1/un donne :
| Année | Population | un+1/un |
|---|---|---|
| 1 | 360 | |
| 2 | 380 | 1,06 |
| 3 | 401 | 1,06 |
| 4 | 423 | 1,06 |
| 5 | 447 | 1,06 |
| 6 | 472 | 1,06 |
| 7 | 498 | 1,06 |
| 8 | 526 | 1,06 |
| 9 | 555 | 1,06 |
| 10 | 586 | 1,06 |
| 11 | 619 | 1,06 |
| 12 | 653 | 1,06 |
| 13 | 689 | 1,06 |
Les rapports sont égaux. La modélisation peut être effectuée par une suite géométrique de premier terme 360 et de raison 1,06.
Zoom sur…
Les limites du modèle de Malthus
En 1798, l'économiste anglais Thomas Malthus publie An essay on the principle of population, dans lequel il émet l'hypothèse que l'accroissement de la population, beaucoup plus rapide que celui des ressources alimentaires, conduira son pays à la famine. Il écrit :« Nous pouvons donc tenir pour certain que, lorsque la population n'est arrêtée par aucun obstacle, elle va doublant tous les vingt-cinq ans, et croît de période en période selon une progression géométrique. […] Nous sommes donc en état de prononcer, en partant de l'état actuel de la terre habitée, que les moyens de subsistance, dans les circonstances les plus favorables de l'industrie, ne peuvent jamais augmenter plus rapidement que selon une progression arithmétique. ».
En 1800, la population de l'Angleterre était estimée à 8 millions d'habitants, et l'agriculture anglaise pouvait nourrir 10 millions de personnes. Le modèle de Malthus admet que la population augmente de 2,8 % chaque année et que les progrès de l'agriculture permettent de nourrir 400 000 personnes de plus chaque année. L'évolution de la population est modélisée par la suite géométrique (un ), où un est le nombre d'habitants (en millions) l'année 1800 + n. Le premier terme de la suite est u0 = 8, et la raison est q = 1,028. L'évolution de l'agriculture est modélisée par une suite arithmétique (vn), où vn correspond au nombre d'habitants qui peuvent être nourris (en millions) l'année 1800 + n. Le premier terme de la suite est v0 = 10, et la raison est r = 0,4. D'où :
un = 8 × 1,028n
vn = 10 + 0,4 × n
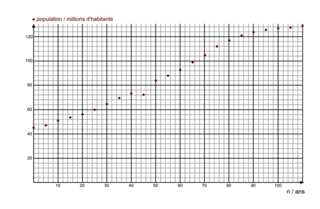 Figure 1. La représentation graphique des deux suites montre une catastrophe en 1846. |
Exercice n°1
A. Quelle est l'expression du taux d'accroissement entre les états un et un+1 ?
Cochez la bonne réponse.
| ||
| ||
|
Le taux d'accroissement est le rapport entre la variation absolue et l'état un , soit :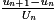 .
.
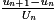 .
.Exercice n°2
Dans une suite arithmétique, quelle proposition est juste ?
Cochez la bonne réponse.
| ||
| ||
|
Les termes pouvant être positifs ou négatifs, ils peuvent également être de plus en plus petits ou garder toujours la même valeur. On passe d'un terme au suivant en additionnant un même nombre, puisque c'est une suite arithmétique.
Exercice n°3
Soit (un) la suite telle que un = 50 − 2n. Quelle proposition est juste ?
Cochez la bonne réponse.
| ||
| ||
|
Par définition, (un) étant une suite arithmétique, la relation générale est : un = u0 + n × r. Le premier terme de la suite est égal à 50. La raison est −2. On calcule u10 = 50 − 2 × 10 = 30.
Exercice n°4
Dans une suite géométrique, quelle proposition est juste ?
Cochez la bonne réponse.
| ||
| ||
|
La raison peut avoir une valeur comprise entre 0 et 1, chaque terme sera alors plus petit que le précédent. On passe d'un terme au suivant en multipliant par un même nombre, puisque c'est une suite géométrique.
Exercice n°5
Que peut-on dire de la suite telle que u1 = 600, u2 = 300, u3 = 150 et u4 = 75 ?
Cochez la bonne réponse.
| ||
| ||
|
Le rapport entre chaque terme donne 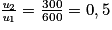 . De même, on trouve
. De même, on trouve 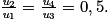 Ainsi, on a une suite géométrique de raison q = 0,5.
Ainsi, on a une suite géométrique de raison q = 0,5.
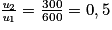 . De même, on trouve
. De même, on trouve 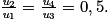 Ainsi, on a une suite géométrique de raison q = 0,5.
Ainsi, on a une suite géométrique de raison q = 0,5.