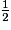Énoncé 1 : un cocktail est composé de 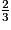 de jus d'orange, de
de jus d'orange, de 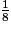 de jus de citron et de sirop de canne.
de jus de citron et de sirop de canne.
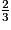 de jus d'orange, de
de jus d'orange, de 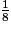 de jus de citron et de sirop de canne.
de jus de citron et de sirop de canne.Quelle part du cocktail représente le sirop de canne ?
• Dans ce cocktail, la part du jus de fruit (orange et citron) est égale à : 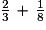 =
= 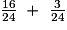 =
= 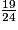 .
.
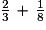 =
= 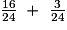 =
= 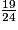 .
.• La part de sirop de canne est donc égale à : 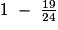 =
= 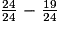 =
= 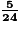 .
.
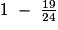 =
= 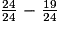 =
= 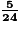 .
.Énoncé 2 : Jean a reçu une somme de son grand-père. Il en dépense d'abord le quart pour s'acheter un livre, puis la moitié du reste pour acheter un disque.
Quelle fraction de la somme de départ a-t-il dépensée ?
• Jean a d'abord dépensé 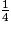 de la somme puis la moitié du reste (reste =
de la somme puis la moitié du reste (reste = 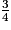 ), c'est-à-dire :
), c'est-à-dire :
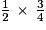 =
= 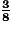 .
.
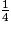 de la somme puis la moitié du reste (reste =
de la somme puis la moitié du reste (reste = 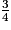 ), c'est-à-dire :
), c'est-à-dire :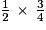 =
= 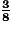 .
.• Jean a donc dépensé en tout 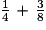 , soit
, soit 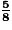 de la somme de départ.
de la somme de départ.
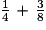 , soit
, soit 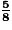 de la somme de départ.
de la somme de départ.Exercice n°1
Madame Hohé a touché les 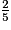 d'un héritage. Elle en a dépensé les
d'un héritage. Elle en a dépensé les 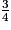 .
.
Quelle partie de l'héritage a-t-elle dépensée ?
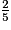 d'un héritage. Elle en a dépensé les
d'un héritage. Elle en a dépensé les 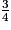 .
.Quelle partie de l'héritage a-t-elle dépensée ?
Cochez la bonne réponse.
| ||
| ||
| ||
|
• Mme Hohé a dépensé les 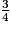 de ce qu'elle a touché. Elle a donc dépensé les
de ce qu'elle a touché. Elle a donc dépensé les 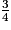 des
des 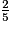 de l'héritage.
de l'héritage.
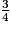 de ce qu'elle a touché. Elle a donc dépensé les
de ce qu'elle a touché. Elle a donc dépensé les 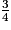 des
des 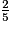 de l'héritage.
de l'héritage.• 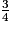 de
de 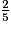 se traduit par la multiplication
se traduit par la multiplication 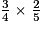 .
.
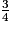 de
de 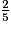 se traduit par la multiplication
se traduit par la multiplication 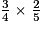 .
.Exercice n°2
Quelle opération correspond à l'énoncé ?
1. Prendre la moitié de 35, puis le tiers du résultat.
Cochez la bonne réponse.
| ||
| ||
|
2. Linda a bu un tiers de litre d'eau et un quart de litre de coca. Quelle quantité de liquide (en litre) a-t-elle bu au total ?
Cochez la bonne réponse.
| ||
| ||
|
1. Quand on cherche une fraction d'une fraction, on effectue une multiplication de fractions.
2. Ici, il s'agit d'additionner deux quantités.
Exercice n°3
Coche la réponse exacte.
a. Quelle fraction représente le tiers du quart de la moitié ?
Cochez la bonne réponse.
| ||
| ||
|
b. Jean marche 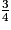 d'heure, se repose
d'heure, se repose 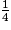 d'heure, puis marche encore
d'heure, puis marche encore 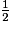 heure.
heure.
Combien de temps s'est-il écoulé entre son départ et son arrivée ?
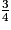 d'heure, se repose
d'heure, se repose 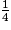 d'heure, puis marche encore
d'heure, puis marche encore 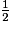 heure.
heure.Combien de temps s'est-il écoulé entre son départ et son arrivée ?
Cochez la bonne réponse.
| ||
| ||
|
a. Quand on cherche une fraction d'une fraction, on effectue une multiplication de fractions.
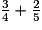
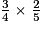
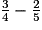
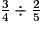
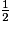 × 3
× 3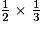
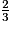
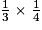
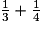
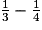
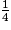 ×
× 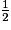
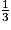 ×
× 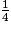 ×
× 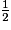
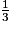 +
+ 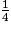 +
+ 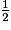
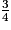 −
− 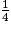 +
+ 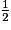
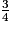 ×
× 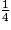 ×
× 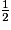
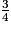 +
+ 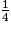 +
+