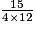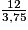Si on a un agrandissement, l'échelle est un nombre supérieur à 1.
Par exemple, pour faire un dessin à l'échelle 2, on a multiplié les dimensions par 2.
Par exemple, pour faire un dessin à l'échelle 2, on a multiplié les dimensions par 2.
Si on a une réduction, l'échelle est un nombre inférieur à 1.
Par exemple, sur une carte à l'échelle 1/10 000, 1 cm représente 10 000 cm dans la réalité (100 m).
Par exemple, sur une carte à l'échelle 1/10 000, 1 cm représente 10 000 cm dans la réalité (100 m).
Règle
Dimensions sur le plan = dimensions réelles × échelle.Problème
Le plan d'une maison est établi à l'échelle 1/20. Quelle est la longueur L sur le plan d'un mur mesurant en réalité 8 m ?
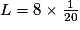
L = 0,40 m = 40 cm
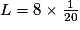
L = 0,40 m = 40 cm
Sur ce même plan, la largeur d'une fenêtre est représentée par un segment de 6 cm. Quelle est sa largeur réelle l ?
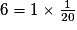
l = 120 cm = 1,20 m
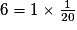
l = 120 cm = 1,20 m
Exercice n°1
Lis les affirmations suivantes.
a. Si je dessine un cercle à l'échelle 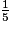 :
:
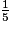 :
: Cochez la bonne réponse.
| ||
| ||
|
b. Si je dessine un cercle à l'échelle 3 :
Cochez la bonne réponse.
| ||
| ||
|
a. Si je fais un dessin à l'échelle 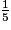 , je divise les dimensions par 5.
, je divise les dimensions par 5.
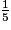 , je divise les dimensions par 5.
, je divise les dimensions par 5. b. Si je fais un dessin à l'échelle 3, je multiplie les dimensions par 3.
Exercice n°2
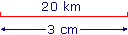 |
L'échelle représentée ici est :
Cochez la bonne réponse.
| ||
| ||
|
20 km = 2 000 000 cm.
Exercice n°3
Sur un dessin fait à l'échelle 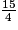 , une longueur mesure 12 cm.
, une longueur mesure 12 cm.
Quelle est sa longueur réelle ?
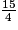 , une longueur mesure 12 cm.
, une longueur mesure 12 cm.Quelle est sa longueur réelle ?
Cochez la bonne réponse.
| ||
| ||
|
Pour trouver la longueur réelle, il suffit de diviser la longueur sur le dessin par l'échelle (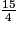 = 3,75).
= 3,75).
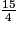 = 3,75).
= 3,75).Exercice n°4
Trouvez la bonne distance.
Écrivez les réponses dans les zones colorées.
a. Sur un plan à l'échelle 1/100, la distance de deux points est 25 cm.
Quelle est leur distance réelle ?
Réponse : cm soit m.
Quelle est leur distance réelle ?
Réponse : cm soit m.
b. Sur ce même plan, par quelle distance est représentée une distance réelle de 8 m ?
Réponse : m, soit cm.
Réponse : m, soit cm.
a. Les dimensions réelles sont 100 fois plus grandes que celles du plan.
25 × 100 = 2 500
2 500 cm = 25 m
25 × 100 = 2 500
2 500 cm = 25 m
b. Les dimensions sur le plan sont 100 fois plus petites que les dimensions réelles.
8 ÷ 100 = 0,08
0,08 m = 8 cm
8 ÷ 100 = 0,08
0,08 m = 8 cm
Exercice n°5
Trouvez la bonne longueur.
Écrivez les réponses dans les zones colorées.
a. Sur un dessin à l'échelle 20, la longueur d'un objet est 4 cm.
Quelle est sa longueur réelle ?
Réponse : cm soit mm.
Quelle est sa longueur réelle ?
Réponse : cm soit mm.
b. Sur ce même dessin, quel est le diamètre d'une roue dentée dont le diamètre réel est 3,5 mm ?
Réponse : mm, soit cm.
Réponse : mm, soit cm.
a. Les dimensions réelles sont 20 fois plus petites que celles du plan.
4 ÷ 20 = 0,2
0,2 cm = 2 mm
4 ÷ 20 = 0,2
0,2 cm = 2 mm
b. Les dimensions sur le plan sont 20 fois plus grandes que les dimensions réelles.
3,5 × 20 = 70
70 mm = 7 cm
3,5 × 20 = 70
70 mm = 7 cm
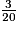
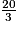
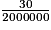
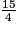 × 12
× 12