Énoncé
Au club « Mathsetmagie », on s’amuse à créer des programmes de calcul plus ou moins magiques.
PARTIE A : le programme de Zoé
Voici le programme de calcul de Zoé :
 |
1. Vérifier que si on choisit 10 comme nombre de départ, on obtient 20 avec ce programme.
2. Quel résultat obtient-t-on avec ce programme si on choisit −7 comme nombre de départ ?
Pour ce programme de calcul, prenez le temps d’effectuer les calculs du programme, étape par étape, en notant tous vos calculs. Chaque étape de calcul rapporte des points, il est important d’être précis et appliqué dans la rédaction.
3. Zoé prétend que son programme est « magique » car, quel que soit le nombre choisi, le résultat est toujours le double du nombre de départ. A-t-elle raison ?
Dans cette question, reprenez le programme de Zoé étape par étape avec le nombre x. À chaque étape, calculer l’expression littérale et la simplifier le plus possible pour faciliter les étapes des calculs suivantes.
PARTIE B : Le programme de Fred
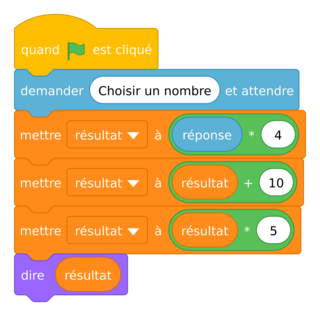
Fred décide de faire son programme de calcul sur Scratch :
4. Démontrer que si le nombre de départ est x, le résultat obtenu avec le programme de Fred est 20x + 50.
5. Quel nombre faut-il choisir au départ pour obtenir 75 avec le programme de Fred ?
 |
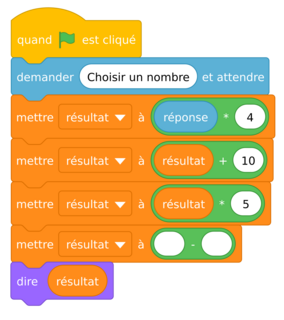
6. Constatant que son programme n’a rien de magique, Fred souhaite le modifier afin que le résultat soit toujours 20 fois plus grand que le nombre de départ. Recopier et compléter sur la copie la sixième ligne du programme pour que ce soit le cas.
 |
Corrigé
PARTIE A : le programme de Zoé
1. On calcule : 10 − 4 = 6, puis 6 × 2 = 12 et enfin 12 + 8 = 20.
On obtient bien 20 en choisissant 10 avec le programme de Zoé.
On obtient bien 20 en choisissant 10 avec le programme de Zoé.
2. On calcule : −7 − 4 = −11, puis −11 × 2 = −22 et enfin −22 + 8 = −14.
On obtient donc −14 en choisissant −7 avec le programme de Zoé.
On obtient donc −14 en choisissant −7 avec le programme de Zoé.
3. On note x le nombre que l’on choisit au départ.
Avec le programme de calcul, on obtient : (x − 4) × 2 + 8 = 2x − 8 + 8 = 2x.
Donc le résultat obtenu est bien le double du nombre de départ.
Avec le programme de calcul, on obtient : (x − 4) × 2 + 8 = 2x − 8 + 8 = 2x.
Donc le résultat obtenu est bien le double du nombre de départ.
PARTIE B : le programme de Fred
4. On note x le nombre que l’on choisit au départ.
Avec le programme de calcul, on obtient : x × 4 + 10 = 4x + 10, et donc pour finir, on a : (4x + 10) × 5 = 20x + 50.
Avec le programme de calcul, on obtient : x × 4 + 10 = 4x + 10, et donc pour finir, on a : (4x + 10) × 5 = 20x + 50.
5. Il faut trouver la valeur de l’inconnue x telle que 20x + 50 = 75.
On résout donc cette équation : 20x = 75 − 50, soit 20x = 25.
On obtient donc finalement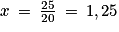 .
.
On résout donc cette équation : 20x = 75 − 50, soit 20x = 25.
On obtient donc finalement
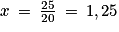 .
.6. Il faut écrire :
 |

