Signaler une erreur
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2025, exercice 3
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2025, exercice 3
Imprimer
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2025, exercice 3
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2025, exercice 3
Énoncé
Cet exercice est un questionnaire à choix multiples (QCM). Aucune justification n'est demandée. Pour chaque question, quatre réponses (A, B, C ou D) sont proposées.
Une seule réponse est exacte. Recopier sur la copie le numéro de la question et la lettre correspondant à la réponse exacte.
Une seule réponse est exacte. Recopier sur la copie le numéro de la question et la lettre correspondant à la réponse exacte.
1.
Le prix de 3 melons est 8,40 €. Combien coûtent 5 melons ?
| A | B | C | D |
| 16,40 € | 42 € | 14 € | 10,40 € |
2.
Quelle transformation permet de passer de la figure 1 à la figure 2 ?
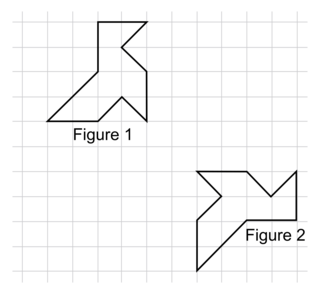 |
| A | B | C | D |
| Une symétrie centrale | Une rotation | Une translation | Une symétrie axiale |
Dans cette question, il faut connaitre les caractéristiques géométriques des transformations géométriques proposées pour observer les figures et bien choisir.
3. Un article coûte 350 €. Son prix augmente de 20 %. Quel est son nouveau prix ?
| A | B | C | D |
| 420 € | 330 € | 370 € | 280 € |
4.
Quelle est l'aire du triangle rectangle ABC ?
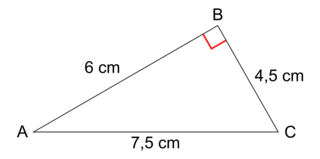 |
| A | B | C | D |
| 27 cm2 | 13,5 cm2 | 18 cm2 | 9 cm2 |
5.
Quelle est la forme développée et réduite de l'expression (2x + 3)(x − 4) ?
| A | B | C | D |
| 2x2 − 5x − 12 | 2x2 − 11x − 12 | 2x2 − 12 | 3x − 1 |
Pour cette question, il est important de faire le calcul du développement étape par étape sans oublier aucun élément.
6.
Quel est le volume de cette pyramide à base rectangulaire ?
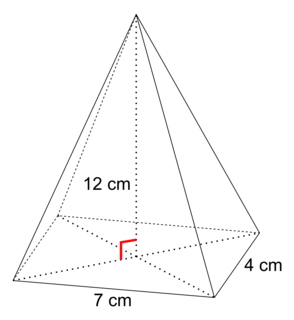 |
| A | B | C | D |
| 23 cm2 | 112 cm2 | 336 cm2 | 168 cm2 |
Corrigé
1. On calcule : 8,4 ÷ 3 = 2,80. Un melon coûte 2,80 €. On calcule ensuite : 2,80 × 5 = 14. Cinq melons coûtent 14 €. Réponse C.
2. Les deux figures étant en miroir l'une de l'autre, la seule transformation qui convient est la symétrie axiale (l'axe traverse la diagonale des carrés qui séparent les deux figures). Réponse D.
3. Quand on augmente un prix de 20 %, cela revient à utiliser le coefficient multiplicateur 1 + 20 % = 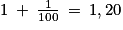 . On calcule le nouveau prix en faisant : 350 × 1,20 = 420 €. Réponse A.
. On calcule le nouveau prix en faisant : 350 × 1,20 = 420 €. Réponse A.
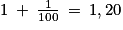 . On calcule le nouveau prix en faisant : 350 × 1,20 = 420 €. Réponse A.
. On calcule le nouveau prix en faisant : 350 × 1,20 = 420 €. Réponse A.4. L'aire d'un triangle rectangle se calcule grâce à la formule : 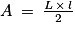 , on obtient donc
, on obtient donc 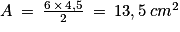 . Réponse B.
. Réponse B.
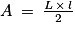 , on obtient donc
, on obtient donc 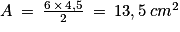 . Réponse B.
. Réponse B.5. On développe l'expression : (2x + 3)(x − 4)= 2x × €x − 2x × 4 + 3 × x − 3 × 4 = 2x2 − 8x + 3x − 12 = 2x2 − 5x − 12. Réponse A.
6. Le volume d'une pyramide se calcule grâce à la formule : 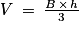 , la base de la pyramide est un rectangle dont l'aire vaut : B = L × l = 7 × 4 = 28 cm2 on obtient
, la base de la pyramide est un rectangle dont l'aire vaut : B = L × l = 7 × 4 = 28 cm2 on obtient 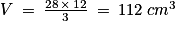 . Réponse B.
. Réponse B.
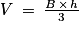 , la base de la pyramide est un rectangle dont l'aire vaut : B = L × l = 7 × 4 = 28 cm2 on obtient
, la base de la pyramide est un rectangle dont l'aire vaut : B = L × l = 7 × 4 = 28 cm2 on obtient 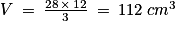 . Réponse B.
. Réponse B.Corrigé
1. On calcule : 8,4 ÷ 3 = 2,80. Un melon coûte 2,80 €. On calcule ensuite : 2,80 × 5 = 14. Cinq melons coûtent 14 €. Réponse C.
2. Les deux figures étant en miroir l'une de l'autre, la seule transformation qui convient est la symétrie axiale (l'axe traverse la diagonale des carrés qui séparent les deux figures). Réponse D.
3. Quand on augmente un prix de 20 %, cela revient à utiliser le coefficient multiplicateur 1 + 20 % = 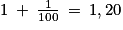 . On calcule le nouveau prix en faisant : 350 × 1,20 = 420 €. Réponse A.
. On calcule le nouveau prix en faisant : 350 × 1,20 = 420 €. Réponse A.
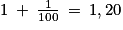 . On calcule le nouveau prix en faisant : 350 × 1,20 = 420 €. Réponse A.
. On calcule le nouveau prix en faisant : 350 × 1,20 = 420 €. Réponse A.4. L'aire d'un triangle rectangle se calcule grâce à la formule : 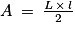 , on obtient donc
, on obtient donc 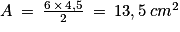 . Réponse B.
. Réponse B.
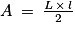 , on obtient donc
, on obtient donc 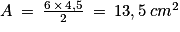 . Réponse B.
. Réponse B.5. On développe l'expression : (2x + 3)(x − 4)= 2x × €x − 2x × 4 + 3 × x − 3 × 4 = 2x2 − 8x + 3x − 12 = 2x2 − 5x − 12. Réponse A.
6. Le volume d'une pyramide se calcule grâce à la formule : 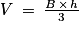 , la base de la pyramide est un rectangle dont l'aire vaut : B = L × l = 7 × 4 = 28 cm2 on obtient
, la base de la pyramide est un rectangle dont l'aire vaut : B = L × l = 7 × 4 = 28 cm2 on obtient 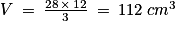 . Réponse B.
. Réponse B.
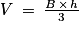 , la base de la pyramide est un rectangle dont l'aire vaut : B = L × l = 7 × 4 = 28 cm2 on obtient
, la base de la pyramide est un rectangle dont l'aire vaut : B = L × l = 7 × 4 = 28 cm2 on obtient 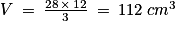 . Réponse B.
. Réponse B.
Signaler une erreur
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2025, exercice 3
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2025, exercice 3
Imprimer
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2025, exercice 3
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2025, exercice 3

