Énoncé
Cette année, les professeurs d'EPS proposent aux élèves un aquathlon (course à pied et natation).
PARTIE A : la course à pied
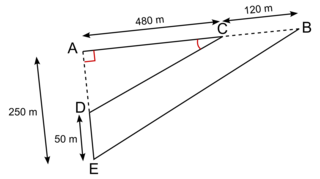
Le parcours de la course à pied est représenté par le dessin ci-dessous (le dessin n'est pas à l'échelle) :
Le parcours est représenté par ACDEB avec le départ au point A et l'arrivée au point B.
Les points A, C, B sont alignés.
Les points A, D, E sont alignés.
ADC est un triangle rectangle en A.
AC = 480 m ; CB = 120 m
AE = 250 m ; DE = 50 m
Le parcours est représenté par ACDEB avec le départ au point A et l'arrivée au point B.
Les points A, C, B sont alignés.
Les points A, D, E sont alignés.
ADC est un triangle rectangle en A.
AC = 480 m ; CB = 120 m
AE = 250 m ; DE = 50 m
 |
1. Justifier que AD = 200 m.
C'est la première question de l'exercice donc il faut utiliser les données de la figure pour continuer l'exercice. Attention à bien justifier la réponse.
2. Calculer la longueur CD.
3.
Pour que le parcours soit validé il est nécessaire que les droites (CD) et (BE) soient parallèles et que la mesure de l'angle 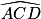 soit supérieure à 20°.
soit supérieure à 20°.
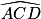 soit supérieure à 20°.
soit supérieure à 20°.a. Les droites (CD) et (BE) sont-elles parallèles ?
b. La mesure de l'angle 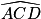 est-elle supérieure à 20° ?
est-elle supérieure à 20° ?
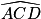 est-elle supérieure à 20° ?
est-elle supérieure à 20° ?Tous les chapitres sont ici utilisés pour résoudre cet exercice. Attention à la rédaction !
c. Le parcours est-il validé ?
PARTIE B : la natation
Concernant l'épreuve de natation, il s'agit de nager une distance de 200 m.
Voici les temps de 9 élèves : 5 min 30 s ; 5 min 45 s ; 5 min 49 s ; 5 min 50 s ; 6 min ; 6 min 11 s ; 6 min 12 s ; 6 min 20 s ; 6 min 40 s.
Voici les temps de 9 élèves : 5 min 30 s ; 5 min 45 s ; 5 min 49 s ; 5 min 50 s ; 6 min ; 6 min 11 s ; 6 min 12 s ; 6 min 20 s ; 6 min 40 s.
4. Quel est le temps médian de cette série ?
Il faut connaitre la définition de la notion de médiane et bien penser à vérifier si les valeurs sont rangées dans l'ordre croissant pour ensuite trouver la valeur centrale de la série.
5. Un poisson rouge nage à la vitesse de 5 km/h. Nage-t-il plus vite que l'élève le plus rapide ?
Pensez à bien convertir cette vitesse pour pouvoir la comparer à celle du poisson rouge et la vitesse de l'élève.
Corrigé
PARTIE A : la course à pied
1. On a AD = AE − DE = 250 − 50 = 200 m.
2. Dans le triangle ADC rectangle en A, le théorème de Pythagore s'écrit : CD2 = AD2 + AC2 ; soit CD2 = 2002 + 4802 = 40 000 + 230 400 = 270 400 ; donc 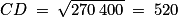 .
.
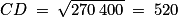 .
.3. a.
Comme les points A, C et B d'une part et les points A, D et E sont alignés dans le même ordre, on cherche si les rapports des longueurs sont égaux pour appliquer la réciproque du théorème de Thalès.
D'une part :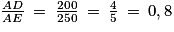 ;
;
D'autre part :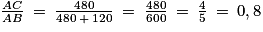 .
.
Ainsi, d'après la réciproque du théorème de Thalès, comme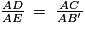 , alors les droites (CD) et (BE) sont parallèles.
, alors les droites (CD) et (BE) sont parallèles.
D'une part :
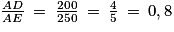 ;
;D'autre part :
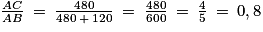 .
.Ainsi, d'après la réciproque du théorème de Thalès, comme
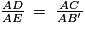 , alors les droites (CD) et (BE) sont parallèles.
, alors les droites (CD) et (BE) sont parallèles.b. Dans le triangle ADC rectangle en A, les formules de trigonométrie permettent d'écrire : 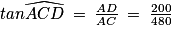 ; soit
; soit 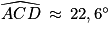 grâce à la calculatrice. Remarque : on pouvait aussi utiliser :
grâce à la calculatrice. Remarque : on pouvait aussi utiliser : 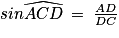 et
et 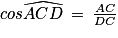 .
.
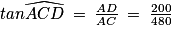 ; soit
; soit 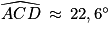 grâce à la calculatrice. Remarque : on pouvait aussi utiliser :
grâce à la calculatrice. Remarque : on pouvait aussi utiliser : 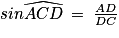 et
et 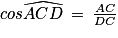 .
.c. D'après les questions précédentes, les droites (CD) et (BE) sont parallèles et l'angle 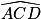 a une mesure supérieure à 20°, donc le parcours sera validé.
a une mesure supérieure à 20°, donc le parcours sera validé.
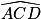 a une mesure supérieure à 20°, donc le parcours sera validé.
a une mesure supérieure à 20°, donc le parcours sera validé.PARTIE B : la natation
5. 9 durées sont rangées dans l'ordre croissant donc le 5e temps partage l'effectif des temps en deux séries de quatre temps. La médiane de la série est donc le 5e temps, c'est-à-dire 6 minutes.
6. L'élève le plus rapide parcourt 200 m soit 0,2 km en 5 min 30.
On convertit : 5 min 30 = 5 × 60 + 30 = 330 s.
Sa vitesse est égale à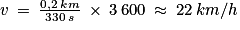 .
.
Le poisson rouge nage donc plus de deux fois plus vite que l'élève le plus rapide.
On convertit : 5 min 30 = 5 × 60 + 30 = 330 s.
Sa vitesse est égale à
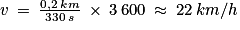 .
.Le poisson rouge nage donc plus de deux fois plus vite que l'élève le plus rapide.

