Sujet de métropole, juin 2025, exercice 1
Énoncé
On dispose d'une urne A contenant 6 boules numérotées : 7 ; 10 ; 12 ; 15 ; 24 ; 30
et d'une urne B contenant 9 boules numérotées : 2 ; 5 ; 6 ; 8 ; 17 ; 18 ; 21 ; 22 ; 25.
Les boules sont indiscernables au toucher.
et d'une urne B contenant 9 boules numérotées : 2 ; 5 ; 6 ; 8 ; 17 ; 18 ; 21 ; 22 ; 25.
Les boules sont indiscernables au toucher.
1.
On tire une boule dans l'urne A, quelle est la probabilité d'obtenir un nombre pair ?
Il faut utiliser la définition d'une probabilité. Soyez vigilant pour bien compter toutes les issues possibles de cette expérience aléatoire.
2. On tire une boule dans l'urne B, justifier que la probabilité d'obtenir un nombre premier est de 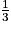 .
.
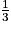 .
.3. Quelle urne contient le plus grand nombre de boules dont le numéro est un multiple de 6 ?
4.
On tire une boule au hasard dans l'une des urnes. Démontrer que la probabilité d'obtenir un nombre supérieur ou égal à 20 est la même quelle que soit l'urne choisie ?
Il faut pouvoir comparer la probabilité que vous allez obtenir dans chaque urne. Pour cela, il faut exprimer les probabilités que vous allez calculer avec le même dénominateur ou sous la forme d'une écriture décimale.
5.
En repartant avec la composition initiale des urnes A et B on décide d'ajouter une boule numérotée 50 dans chacune d'entre elles. Dans ces conditions, la probabilité d'obtenir un résultat supérieur ou égal à 20 est-t-elle toujours égale quelle que soit l'urne choisie ?
Il ne faut pas se précipiter au risque d'inscrire une réponse sans calculer les nouvelles probabilités. Dans ce cas, la définition d'une probabilité ne serait pas donnée. Il est important de prendre son temps, de lister les issues et de recalculer les probabilités avant de répondre.
Annexes
© 2000-2026, Miscellane
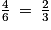 .
.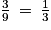 .
.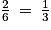 .
.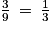 .
.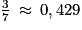 .
.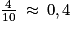 .
.