Énoncé
17 points
Les questions 1 et 2 sont indépendantes.
Un sablier est composé de :
Un sablier est composé de :
- deux cylindres C1 et C2 de hauteur 4,2 cm et de diamètre 1,5 cm ;
- un cylindre C3 ;
- deux demi-sphères S1 et S2 de diamètre 1,5 cm.
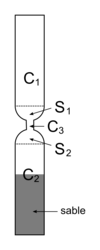 |
On rappelle le volume V d'un cylindre d'aire de base B et de hauteur h : V = B × h.
1.
a) Au départ, le sable remplit le cylindre C2 aux deux tiers. Montrer que le volume du sable est environ 4,95 cm3.
À nouveau, il est recommandé de noter les mesures sur le schéma du sablier.
Vous devez faire attention pour le calcul du volume du cylindre : il faut calculer l'aire de la base du cylindre, en utilisant la formule de l'aire d'un disque.
Dans la formule de l'aire d'un disque, vous devrez utiliser le rayon du disque et pas le diamètre donné dans l'énoncé.
Vous devez faire attention pour le calcul du volume du cylindre : il faut calculer l'aire de la base du cylindre, en utilisant la formule de l'aire d'un disque.
Dans la formule de l'aire d'un disque, vous devrez utiliser le rayon du disque et pas le diamètre donné dans l'énoncé.
b) On retourne le sablier. En supposant que le débit d'écoulement du sable est constant et égal à 1,98 cm3/min, calculer le temps en minutes et secondes que va mettre le sable à s'écouler dans le cylindre inférieur.
Pensez à convertir les minutes en secondes pour éviter d'avoir des nombres décimaux et de vous tromper dans les calculs de temps.
Le débit étant une situation de proportionnalité, n'hésitez pas à construire un tableau de proportionnalité pour vous aider dans vos calculs.
Le débit étant une situation de proportionnalité, n'hésitez pas à construire un tableau de proportionnalité pour vous aider dans vos calculs.
2. En réalité, le débit d'écoulement d'un même sablier n'est pas constant.
Dans une usine où on fabrique des sabliers comme celui-ci, on prend un sablier au hasard et on teste plusieurs fois le temps d'écoulement dans ce sablier. Voici les différents temps récapitulés dans le tableau suivant :
Dans une usine où on fabrique des sabliers comme celui-ci, on prend un sablier au hasard et on teste plusieurs fois le temps d'écoulement dans ce sablier. Voici les différents temps récapitulés dans le tableau suivant :
| Temps mesuré | 2 min 22 s | 2 min 24 s | 2 min 26 s | 2 min 27 s | 2 min 28 s | 2 min 29 s | 2 min 30 s |
| Nombre de tests | 1 | 1 | 2 | 6 | 3 | 7 | 6 |
| Temps mesuré | 2 min 31 s | 2 min 32 s | 2 min 33 s | 2 min 34 s | 2 min 35 s | 2 min 38 s |
| Nombre de tests | 3 | 1 | 2 | 3 | 2 | 3 |
a) Combien de tests ont été réalisés au total ?
Pensez à justifier votre réponse (par exemple, avec un calcul).
b) Un sablier est mis en vente s'il vérifie les trois conditions ci-après, sinon il est éliminé.
- L'étendue des temps est inférieure à 20 s.
- La médiane des temps est comprise entre 2 min 29 s et 2 min 31 s.
- La moyenne des temps est comprise entre 2 min 28 s et 2 min 32 s.
Vous devez écrire tous les calculs pour justifier chacune de vos réponses.
Vous devez connaître la différence entre une médiane et une moyenne. La médiane représente la valeur au milieu de la série, c'est-à-dire la valeur centrale telle que la moitié des valeurs de la série sont supérieures ou égales à la médiane, et la moitié lui sont inférieures ou égales. La moyenne d'une série représente la valeur que tous les termes de la série devraient prendre pour un partage équitable.
Dans cette série, le mélange des unités peut provoquer des erreurs de calculs, il est donc recommandé de transformer les durées en ne gardant que des secondes pour simplifier les calculs et n'avoir qu'une unité.
Vous devez connaître la différence entre une médiane et une moyenne. La médiane représente la valeur au milieu de la série, c'est-à-dire la valeur centrale telle que la moitié des valeurs de la série sont supérieures ou égales à la médiane, et la moitié lui sont inférieures ou égales. La moyenne d'une série représente la valeur que tous les termes de la série devraient prendre pour un partage équitable.
Dans cette série, le mélange des unités peut provoquer des erreurs de calculs, il est donc recommandé de transformer les durées en ne gardant que des secondes pour simplifier les calculs et n'avoir qu'une unité.
Corrigé
1.
a) On calcule le volume du cylindre C2 et on utilise la formule : V = B × h.
Dans le cylindre, l'aire de la base est donnée par la formule :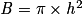 .
.
On a donc besoin du rayon du cylindre :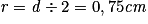 .
.
Donc on calcule le volume de C2 :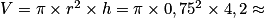 7,42 cm3.
7,42 cm3.
Comme le sable remplit le cylindre aux deux tiers :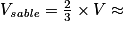 4,95 cm3.
4,95 cm3.
Dans le cylindre, l'aire de la base est donnée par la formule :
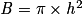 .
.On a donc besoin du rayon du cylindre :
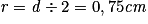 .
.Donc on calcule le volume de C2 :
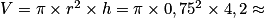 7,42 cm3.
7,42 cm3.Comme le sable remplit le cylindre aux deux tiers :
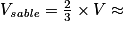 4,95 cm3.
4,95 cm3.b) On sait que le débit du sablier est de 1,98 cm3 en 1 min donc 1,98 cm3 en 60 s.
On peut construire le tableau de proportionnalité :
On fait un produit en croix :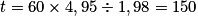 .
.
Donc il faut 150 secondes, c'est-à-dire 2 min 30 s pour que le sable s'écoule complètement entre les deux cylindres.
On peut construire le tableau de proportionnalité :
| Volume de sable (en cm3) | 1,98 | 4,95 |
| Temps (en sec) | 60 | |
On fait un produit en croix :
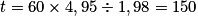 .
.Donc il faut 150 secondes, c'est-à-dire 2 min 30 s pour que le sable s'écoule complètement entre les deux cylindres.
2.
a) Au total, il y a eu 40 tests de réalisés dans l'usine.
b) L'étendue de ces tests : e 2 min 38 sec − 2 min 22 sec = 16 sec. Donc l'étendue est bien inférieure à 20 secondes.
La médiane de ces tests : il y a 40 tests donc on partage la série en deux groupes de 20 valeurs. La médiane s'obtient donc entre la 20e et la 21e valeur. La 20e valeur est 2 min 29 s, et la 21e valeur est 2 min 30 s, donc la médiane est entre 2 min 29 s et 2 min 30 s. Donc la médiane est bien comprise entre 2 min 29 s et 2 min 31 s.
La moyenne de cette série se calcule en mettant toutes les valeurs dans la même unité, donc on transforme tous les temps pour les mettre uniquement en secondes.
2 min 22 s = 142 s ; 2 min 24 s = 144 s ; … ; 2 min 38 s = 158 s.
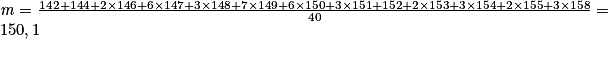 .
.
La moyenne est donc d'environ 150 s, soit 2 min 30 s. La moyenne est bien comprise entre 2 min 28 s et 2 min 32 s. Comme les trois conditions sont réunies, le sablier testé ne sera pas éliminé.
La médiane de ces tests : il y a 40 tests donc on partage la série en deux groupes de 20 valeurs. La médiane s'obtient donc entre la 20e et la 21e valeur. La 20e valeur est 2 min 29 s, et la 21e valeur est 2 min 30 s, donc la médiane est entre 2 min 29 s et 2 min 30 s. Donc la médiane est bien comprise entre 2 min 29 s et 2 min 31 s.
La moyenne de cette série se calcule en mettant toutes les valeurs dans la même unité, donc on transforme tous les temps pour les mettre uniquement en secondes.
2 min 22 s = 142 s ; 2 min 24 s = 144 s ; … ; 2 min 38 s = 158 s.
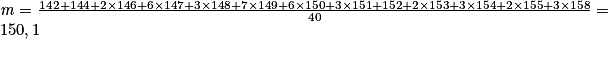 .
.La moyenne est donc d'environ 150 s, soit 2 min 30 s. La moyenne est bien comprise entre 2 min 28 s et 2 min 32 s. Comme les trois conditions sont réunies, le sablier testé ne sera pas éliminé.

