Énoncé
17 points
Le hand-spinner est une sorte de toupie plate qui tourne sur elle-même.
 |
On donne au hand-spinner une vitesse de rotation initiale au temps t = 0, puis, au cours du temps, sa vitesse de rotation diminue jusqu'à l'arrêt complet du hand-spinner. Sa vitesse de rotation est alors égale à 0.
Grâce à un appareil de mesure, on a relevé la vitesse de rotation exprimée en nombre de tours par seconde.
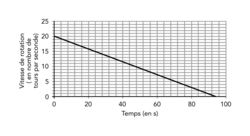
Sur le graphique ci-dessous, on a représenté cette vitesse en fonction du temps exprimé en seconde :
Grâce à un appareil de mesure, on a relevé la vitesse de rotation exprimée en nombre de tours par seconde.
Sur le graphique ci-dessous, on a représenté cette vitesse en fonction du temps exprimé en seconde :
 |
1.
Le temps et la vitesse de rotation du hand-spinner sont-ils proportionnels ? Justifier.
Rappelez-vous du lien qui existe entre situation de proportionnalité et représentation graphique.
2.
Par lecture graphique, répondre aux questions suivantes :
a)
Quelle est la vitesse de rotation initiale du hand-spinner (en nombre de tours par seconde) ?
Remarquez qu'il s'agit de déterminer l'ordonnée y du point de la droite qui a pour abscisse t = 0.
b)
Quelle est la vitesse de rotation du hand-spinner (en nombre de tours par seconde) au bout de 1 minute et 20 secondes ?
Remarquez que 1 min 20 s= 80 s.
c)
Au bout de combien de temps, le hand-spinner va-t-il s'arrêter ?
Remarquez qu'il s'agit de déterminer l'abscisse t du point de la droite qui a pour ordonnée y = 0.
3.
Pour calculer la vitesse de rotation du hand-spinner en fonction du temps t, notée V(t), on utilise la fonction suivante :
V(t) = −0,214 × t + Vinitiale
V(t) = −0,214 × t + Vinitiale
- t est le temps (exprimé en seconde) qui s'est écoulé depuis le début de la rotation du hand-spinner.
- Vinitiale est la vitesse de rotation à laquelle on a lancé le hand-spinner au départ.
a)
On lance le hand-spinner à une vitesse initiale de 20 tours par seconde. Sa vitesse de rotation est donc donnée par la formule : V(t) = −0,214 × t + 20. Calculer sa vitesse de rotation au bout de 30 s.
Il s'agit de calculer V(30).
b)
Au bout de combien de temps le hand-spinner va-t-il s'arrêter ? Justifier par un calcul.
Remarquez qu'il s'agit de déterminer, par le calcul, le temps t tel que V(t) = 0.
c)
Est-il vrai que, d'une manière générale, si l'on fait tourner le hand-spinner deux fois plus vite au départ, il tournera deux fois plus longtemps ? Justifier.
Modifiez l'expression V(t) et résolvez la nouvelle équation V(t) = 0.
Corrigé
1.
Une situation de proportionnalité est représentée graphiquement par une droite qui passe par l'origine.
Ici, la courbe représentative est une droite, mais elle ne passe pas par l'origine du repère. Le temps et la vitesse de rotation du hand-spinner ne sont donc pas proportionnels.
Ici, la courbe représentative est une droite, mais elle ne passe pas par l'origine du repère. Le temps et la vitesse de rotation du hand-spinner ne sont donc pas proportionnels.
2.
a)
Graphiquement, la vitesse de rotation initiale du hand-spinner est de 20 tours par seconde.
b)
1 min 20 s= 80 s.
Graphiquement, au bout de 80 s, la vitesse de rotation du hand-spinner est de 3 tours par seconde.
Graphiquement, au bout de 80 s, la vitesse de rotation du hand-spinner est de 3 tours par seconde.
c)
Graphiquement, lorsque le hand-spinner s'arrête, l'ordonnée du point de la droite est y = 0 et son abscisse est approximativement x = 94.
Le hand-spinner va donc s'arrêter au bout de 94 s = 1 min 34 s.
De la figure complétée, on déduit que la valeur mise dans la variable « Longueur » à la ligne 9 est 300 − 2 × 50 = 300 − 100 = 200.
Le hand-spinner va donc s'arrêter au bout de 94 s = 1 min 34 s.
De la figure complétée, on déduit que la valeur mise dans la variable « Longueur » à la ligne 9 est 300 − 2 × 50 = 300 − 100 = 200.
3.
a)
La vitesse de rotation (en tours par seconde) est donnée par la formule : V(t) = −0,214 × t + 20 où t est exprimé en seconde.
La vitesse de rotation du hand-spinner au bout de 30 s est donc V(30) = −0,214 × 30 + 20 = −6,42 + 20 = 13,58 tours par seconde.
La vitesse de rotation du hand-spinner au bout de 30 s est donc V(30) = −0,214 × 30 + 20 = −6,42 + 20 = 13,58 tours par seconde.
b)
Lorsque le hand-spinner s'arrête, on a V(t) = 0 car sa vitesse de rotation est nulle.
On a donc −0,214 × t + 20 = 0, puis 0,214 × t = 20 et t =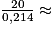
93,5 s au dixième près.
Le hand-spinner va donc s'arrêter au bout d'environ 94 s.
On a donc −0,214 × t + 20 = 0, puis 0,214 × t = 20 et t =
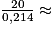93,5 s au dixième près.Le hand-spinner va donc s'arrêter au bout d'environ 94 s.
c)
Si l'on fait tourner le hand-spinner deux fois plus vite au départ, la vitesse de rotation (en tours par seconde) est donnée par la formule :
V(t) = −0,214 × t + 40 où t est exprimé en seconde.
Lorsque le hand-spinner s'arrête, on a V(t) = 0 donc :
−0,214 × t + 40 = 0, puis 0,214 × t = 40 et t =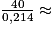
186,9 s au dixième près.
On a bien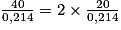
.
Il est donc vrai que si l'on fait tourner le hand-spinner deux fois plus vite au départ, il tournera deux fois plus longtemps.
V(t) = −0,214 × t + 40 où t est exprimé en seconde.
Lorsque le hand-spinner s'arrête, on a V(t) = 0 donc :
−0,214 × t + 40 = 0, puis 0,214 × t = 40 et t =
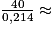186,9 s au dixième près.On a bien
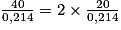. Il est donc vrai que si l'on fait tourner le hand-spinner deux fois plus vite au départ, il tournera deux fois plus longtemps.
