Sujet de métropole, juin 2016, exercice 6
Énoncé
7 points
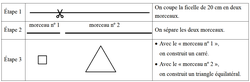
Avec des ficelles de 20 cm, on construit des polygones comme ci-dessous :
 |
Partie 1
Dans cette partie, on découpe à l'étape 1 une ficelle pour que le « morceau nº 1 » mesure 8 cm.
1.
Dessiner en grandeur réelle les deux polygones obtenus.
Pour connaître le côté du carré construit avec le « morceau nº 1 », exprimez le côté d'un carré en fonction de son périmètre.
Pour connaître le côté du triangle équilatéral construit avec le « morceau nº 2 », exprimez le côté d'un triangle équilatéral en fonction de son périmètre.
Pour connaître le côté du triangle équilatéral construit avec le « morceau nº 2 », exprimez le côté d'un triangle équilatéral en fonction de son périmètre.
2.
Calculer l'aire du carré obtenu.
Rappelez-vous que l'aire d'un carré de côté c est c2.
3.
Estimer l'aire du triangle équilatéral obtenu en mesurant sur le dessin.
Tracez la hauteur de ce triangle équilatéral pour pouvoir la mesurer.
Partie 2
Dans cette partie, on cherche maintenant à étudier l'aire des deux polygones obtenus à l'étape 3 en fonction de la longueur du « morceau nº 1 ».
1.
Proposer une formule qui permet de calculer l'aire du carré en fonction de la longueur du « morceau nº 1 ».
Notez x la longueur (en cm) du « morceau nº 1 » et exprimez le côté d'un carré en fonction de son périmètre, puis son aire en fonction de son périmètre.
2.
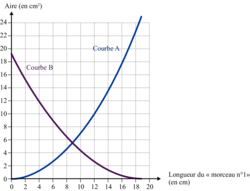
Sur le graphique ci-dessous :
- la courbe A représente la fonction qui donne l'aire du carré en fonction de la longueur du « morceau nº 1 » ;
- la courbe B représente la fonction qui donne l'aire du triangle équilatéral en fonction de la longueur du « morceau nº 1 ».
 |
En utilisant ce graphique, répondre aux questions suivantes. Aucune justification n'est attendue.
a)
Quelle est la longueur du « morceau nº 1 » qui permet d'obtenir un triangle équilatéral d'aire 14 cm2 ?
Vous devez trouver cette valeur à l'aide de la courbe B.
b)
Quelle est la longueur du « morceau nº 1 » qui permet d'obtenir deux polygones d'aires égales ?
Il s'agit de déterminer l'abscisse du point d'intersection des courbes A et B.
Annexes
© 2000-2026, Miscellane
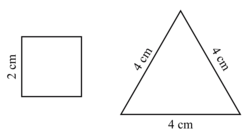
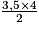 = 3,5 × 2 = 7 cm2.
= 3,5 × 2 = 7 cm2. 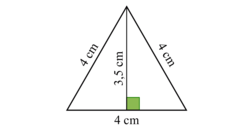
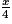 .
. 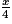 , l'aire de ce carré a pour expression
, l'aire de ce carré a pour expression 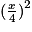 =
= 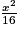 .
.