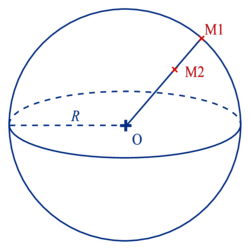
• Soit une sphère de centre O et de rayon R :
- si on a un point M1 tel que OM1 = R alors M1 est sur la sphère ;
- si on a un point M2 tel que OM2
 R alors M2 appartient à la boule.
R alors M2 appartient à la boule.
 |
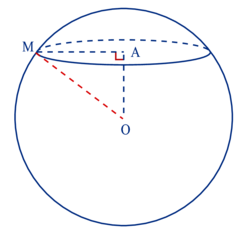
• La section d'une sphère par un plan est un cercle.
Pour déterminer son rayon, on applique la propriété de Pythagore.
A étant le centre de la section, AM son rayon et OM le rayon de la sphère, on a : OM2 = AM2 + OA2.
On en déduit facilement le rayon de la section AM.
Pour déterminer son rayon, on applique la propriété de Pythagore.
A étant le centre de la section, AM son rayon et OM le rayon de la sphère, on a : OM2 = AM2 + OA2.
On en déduit facilement le rayon de la section AM.
 |
Exercice n°1
Détermine la bonne réponse.
Faites glisser les étiquettes dans les zones prévues à cet effet.
faux
vrai
je ne sais pas
1. Figure 1 :
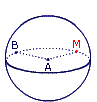 |
→ M est un point de la boule de rayon [AB] :
→ M est un point de la sphère de rayon [AB] :
→ M est situé hors de la boule de rayon [AB] :
imcAnswer1|imcAnswer2|imcAnswer6|imcAnswer7?
.→ M est un point de la sphère de rayon [AB] :
imcAnswer1|imcAnswer2|imcAnswer6|imcAnswer7?
.→ M est situé hors de la boule de rayon [AB] :
imcAnswer3|imcAnswer4|imcAnswer5|imcAnswer9?
. 2. Figure 2 :
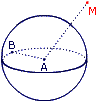 |
→ M est un point de la boule de rayon [AB] :
→ M est un point de la sphère de rayon [AB] :
→ M est situé hors de la boule de rayon [AB] :
imcAnswer3|imcAnswer4|imcAnswer5|imcAnswer9?
.→ M est un point de la sphère de rayon [AB] :
imcAnswer3|imcAnswer4|imcAnswer5|imcAnswer9?
.→ M est situé hors de la boule de rayon [AB] :
imcAnswer1|imcAnswer2|imcAnswer6|imcAnswer7?
. 3. Figure 3 :
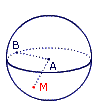 |
→ M est un point de la boule de rayon [AB] :
→ M est un point de la sphère de rayon [AB] :
→ M est situé hors de la boule de rayon [AB] :
imcAnswer1|imcAnswer2|imcAnswer6|imcAnswer7?
.→ M est un point de la sphère de rayon [AB] :
imcAnswer8?
.→ M est situé hors de la boule de rayon [AB] :
imcAnswer3|imcAnswer4|imcAnswer5|imcAnswer9?
.• Figure 1 : la distance AM est égale au rayon.
• Figure 2 : la distance AM est supérieure au rayon.
• Figure 3 : la distance AM est inférieure ou égale au rayon.
Exercice n°2
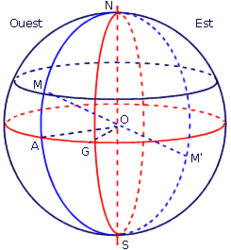 |
Le point G est sur le méridien de Greenwich.
Le point A est sur l'équateur.
Les coordonnées du point M sont 20° Ouest et 30° Nord.
Le point M' est diamétralement opposé au point M.
Le point A est sur l'équateur.
Les coordonnées du point M sont 20° Ouest et 30° Nord.
Le point M' est diamétralement opposé au point M.
Détermine les coordonnées géographiques de A, G et M'.
Écrivez les réponses dans les zones colorées.
| | Longitude | Latitude |
| A | ° Ouest | ° |
| G | ° | ° |
| M' | ° Est | ° Sud |
Les points A et M sont sur le même méridien.
Le méridien de Greenwich est le méridien origine.
Le point M' est dans l'hémisphère Sud.
Le méridien de Greenwich est le méridien origine.
Le point M' est dans l'hémisphère Sud.
Exercice n°3
Voici les coordonnées géographiques approximatives de quatre villes :
| | Longitude | Latitude |
| Acapulco | 100° Ouest | 16° Nord |
| Monterrey | 100° Ouest | 25° Nord |
| Denver | 105° Ouest | 40° Nord |
| Philadelphie | 75° Ouest | 40° Nord |
Écrivez les réponses dans les zones colorées.
a. Complète en utilisant les mots méridien ou parallèle.
→ Les villes de Monterrey et Acapulco sont approximativement situées sur le même .
→ Les villes de Denver et Philadelphie sont approximativement situées sur le même .
→ Les villes de Monterrey et Acapulco sont approximativement situées sur le même .
→ Les villes de Denver et Philadelphie sont approximativement situées sur le même .
b. La longueur de l'équateur mesure environ 40 000 km.
Quelle est la distance entre Monterrey et Acapulco ? km
Quelle est la distance entre Monterrey et Acapulco ? km
b. D'après les données du tableau, Monterrey et Acapulco sont situées sur le même méridien et forment un angle de 9° avec le centre de la Terre.
Distance entre les deux villes :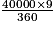 = 1000 ; soit 1000 km.
= 1000 ; soit 1000 km.
Distance entre les deux villes :
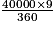 = 1000 ; soit 1000 km.
= 1000 ; soit 1000 km.Exercice n°4
Soit (S) une sphère de centre O et de 5 cm de rayon.
Les affirmations suivantes sont-elles vraies ou fausses ?
Coche la bonne réponse.
Coche la bonne réponse.
a. Si M est un point tel que OM = 5 cm alors M est à l'extérieur de la boule délimitée par (S).
Cochez la bonne réponse.
| ||
|
b. Si M est un point tel que OM = 6 cm alors M est à l'extérieur de la boule délimitée par (S).
Cochez la bonne réponse.
| ||
|
c. Le rayon de la section de la sphère (S) par un plan peut être égal à 7 cm.
Cochez la bonne réponse.
| ||
|
a. M est sur la sphère.
c. Le rayon de la section de la sphère (S) par un plan est inférieur ou égal à 5 cm.

