Principe d'inertie
Fiche
Le principe de l'inertie, aussi appelé première loi de Newton, est l'un des fondements de la mécanique classique. Son énoncé historique est : « Tout corps persévère dans son état de repos ou de mouvement rectiligne uniforme, sauf si des forces "imprimées" le contraignent d'en changer. » Cet énoncé figure dans les premières pages du traité de Newton.
I. Le principe d'inertie
• Une force est la modélisation d'une action mécanique qui s'exerce sur un système et qui peut modifier le mouvement du système : elle peut donc modifier la valeur de la vitesse et elle peut également modifier la direction du mouvement.
• Le principe de l'inertie permet de relier les forces à la nature du mouvement. Dans son énoncé actuel, le principe de l'inertie stipule : « Lorsque les forces qui s'exercent sur un solide se compensent, son centre d'inertie persévère en son état de repos ou de mouvement rectiligne uniforme, 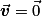 ou
ou 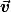 est un vecteur constant. »
est un vecteur constant. »
« Réciproquement, si le centre d'inertie d'un solide isolé ou pseudo isolé persévère en son état de repos ou de mouvement rectiligne uniforme, c'est-à-dire si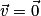 ou
ou 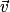 est un vecteur constant, alors les forces qui s'exercent sur lui se compensent. »
est un vecteur constant, alors les forces qui s'exercent sur lui se compensent. »
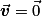 ou
ou 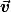 est un vecteur constant. »
est un vecteur constant. »« Réciproquement, si le centre d'inertie d'un solide isolé ou pseudo isolé persévère en son état de repos ou de mouvement rectiligne uniforme, c'est-à-dire si
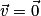 ou
ou 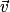 est un vecteur constant, alors les forces qui s'exercent sur lui se compensent. »
est un vecteur constant, alors les forces qui s'exercent sur lui se compensent. »• La somme des forces se note 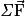 , et le fait que les forces se compensent signifie que leur somme vectorielle est nulle :
, et le fait que les forces se compensent signifie que leur somme vectorielle est nulle : 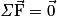 . On appelle
. On appelle 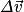 la variation du vecteur vitesse. Ainsi le principe de l'inertie et sa réciproque peuvent se résumer par :
la variation du vecteur vitesse. Ainsi le principe de l'inertie et sa réciproque peuvent se résumer par :
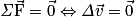 c'est-à-dire que
c'est-à-dire que 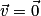 ou
ou 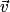 est un vecteur constant.
est un vecteur constant.
Exemples :
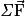 , et le fait que les forces se compensent signifie que leur somme vectorielle est nulle :
, et le fait que les forces se compensent signifie que leur somme vectorielle est nulle : 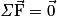 . On appelle
. On appelle 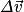 la variation du vecteur vitesse. Ainsi le principe de l'inertie et sa réciproque peuvent se résumer par :
la variation du vecteur vitesse. Ainsi le principe de l'inertie et sa réciproque peuvent se résumer par :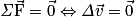 c'est-à-dire que
c'est-à-dire que 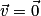 ou
ou 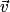 est un vecteur constant.
est un vecteur constant.Exemples :
- un solide est immobile et soumis à trois forces
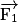 ,
, 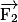 et
et 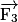 . D'après le principe d'inertie, comme la vitesse de ce solide est nulle alors
. D'après le principe d'inertie, comme la vitesse de ce solide est nulle alors 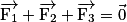 ;
; - un skieur glisse sur une piste enneigée. Il n'est soumis qu'à son poids
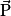 et à la réaction du support
et à la réaction du support 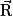 , les autres forces étant négligeables. Son poids compense la réaction du support de telle sorte que l'on peut écrire :
, les autres forces étant négligeables. Son poids compense la réaction du support de telle sorte que l'on peut écrire : 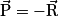 ou en transposant,
ou en transposant, 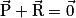 . Donc d'après le principe d'inertie, comme les forces qui s'exercent sur le skieur se compensent alors son vecteur vitesse est constant.
. Donc d'après le principe d'inertie, comme les forces qui s'exercent sur le skieur se compensent alors son vecteur vitesse est constant.
• Le principe d'inertie permet de définir les référentiels galiléens : un référentiel sera dit galiléen si le principe d'inertie y est réalisé. Le référentiel terrestre est supposé galiléen.
Exercice n°1Exercice n°2
Exercice n°1Exercice n°2
II. La contraposée du principe d'inertie
• Tout système soumis à des forces qui ne se compensent pas n'est ni immobile, ni en mouvement rectiligne uniforme, donc la variation du vecteur vitesse n'est pas nulle. Et réciproquement si entre deux instants voisins, le vecteur vitesse 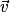 d'un système varie, alors les forces qui s'exercent sur le système ne se compensent pas.
d'un système varie, alors les forces qui s'exercent sur le système ne se compensent pas.
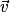 d'un système varie, alors les forces qui s'exercent sur le système ne se compensent pas.
d'un système varie, alors les forces qui s'exercent sur le système ne se compensent pas.• On peut résumer la contraposée du principe d'inertie par :
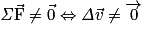 c'est-à-dire que
c'est-à-dire que 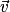 varie.
varie.
Avec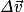 la variation du vecteur vitesse et
la variation du vecteur vitesse et 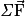 la somme vectorielle des forces qui s'exercent sur le système.
la somme vectorielle des forces qui s'exercent sur le système.
Exemple : un joueur de pétanque fait rouler sa boule. Elle s'arrête au bout de quelques mètres. On supposera qu'elle n'est soumise qu'à son poids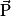 , à la réaction du support
, à la réaction du support 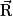 et à la force de frottement du sol
et à la force de frottement du sol 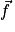 . Les frottements de l'air sont négligés. Comme sa vitesse varie (elle s'arrête au bout de quelques mètres), alors d'après la contraposée du principe d'inertie les forces qui s'exercent sur la boule ne se compensent pas, donc on peut écrire :
. Les frottements de l'air sont négligés. Comme sa vitesse varie (elle s'arrête au bout de quelques mètres), alors d'après la contraposée du principe d'inertie les forces qui s'exercent sur la boule ne se compensent pas, donc on peut écrire : 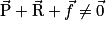 .
.
Exercice n°3
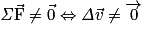 c'est-à-dire que
c'est-à-dire que 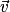 varie.
varie.Avec
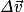 la variation du vecteur vitesse et
la variation du vecteur vitesse et 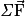 la somme vectorielle des forces qui s'exercent sur le système.
la somme vectorielle des forces qui s'exercent sur le système.Exemple : un joueur de pétanque fait rouler sa boule. Elle s'arrête au bout de quelques mètres. On supposera qu'elle n'est soumise qu'à son poids
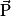 , à la réaction du support
, à la réaction du support 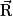 et à la force de frottement du sol
et à la force de frottement du sol 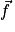 . Les frottements de l'air sont négligés. Comme sa vitesse varie (elle s'arrête au bout de quelques mètres), alors d'après la contraposée du principe d'inertie les forces qui s'exercent sur la boule ne se compensent pas, donc on peut écrire :
. Les frottements de l'air sont négligés. Comme sa vitesse varie (elle s'arrête au bout de quelques mètres), alors d'après la contraposée du principe d'inertie les forces qui s'exercent sur la boule ne se compensent pas, donc on peut écrire : 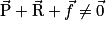 .
.Exercice n°3
III. La chute libre verticale sans frottements
• Tout système qui a un mouvement rectiligne et qui n'est soumis qu'à son poids est dit en chute libre. Dans la pratique, il suffit de pouvoir négliger l'intensité des forces de frottement devant l'intensité du poids.
• D'après la contraposée du principe d'inertie, un système qui n'est soumis qu'à une force, le poids, a un vecteur vitesse qui varie : 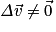 . Donc, un système en chute libre verticale a un mouvement rectiligne non uniforme.
. Donc, un système en chute libre verticale a un mouvement rectiligne non uniforme.
On peut résumer cela par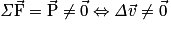 ,
,
avec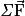 la somme vectorielle des forces qui s'exercent sur le système
la somme vectorielle des forces qui s'exercent sur le système 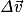 et la variation du vecteur vitesse.
et la variation du vecteur vitesse.
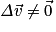 . Donc, un système en chute libre verticale a un mouvement rectiligne non uniforme.
. Donc, un système en chute libre verticale a un mouvement rectiligne non uniforme.On peut résumer cela par
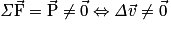 ,
,avec
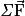 la somme vectorielle des forces qui s'exercent sur le système
la somme vectorielle des forces qui s'exercent sur le système 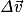 et la variation du vecteur vitesse.
et la variation du vecteur vitesse.• Le mouvement est accéléré si le vecteur vitesse 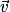 a même sens que le poids
a même sens que le poids 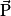 et il est ralenti si le vecteur vitesse
et il est ralenti si le vecteur vitesse 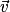 et le poids
et le poids 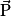 sont de sens opposés.
sont de sens opposés.
Exemples :
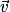 a même sens que le poids
a même sens que le poids 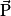 et il est ralenti si le vecteur vitesse
et il est ralenti si le vecteur vitesse 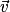 et le poids
et le poids 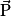 sont de sens opposés.
sont de sens opposés.Exemples :
- Un enfant lance verticalement vers le haut une balle de tennis. La vitesse de la balle est dirigée vers le haut et le poids est de sens opposé. Le mouvement de la balle est donc rectiligne ralenti durant son ascension.
- Un enfant laisse tomber une balle de tennis verticalement. La vitesse de la balle est dirigée vers le bas et le poids est de même sens que le vecteur vitesse. Le mouvement de la balle est donc rectiligne accéléré.
IV. La chute libre verticale avec frottements
• Lors d'une chute, lorsque les frottements ne sont plus négligeables, le système est alors soumis à deux forces : son poids 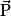 et la force de frottement
et la force de frottement 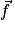 . Ces deux forces sont de même direction et de sens opposés. Si la force de frottement compense le poids, alors d'après le principe d'inertie la variation du vecteur vitesse du système est nulle, c'est-à-dire que le vecteur vitesse reste constant. Le mouvement devient rectiligne uniforme.
. Ces deux forces sont de même direction et de sens opposés. Si la force de frottement compense le poids, alors d'après le principe d'inertie la variation du vecteur vitesse du système est nulle, c'est-à-dire que le vecteur vitesse reste constant. Le mouvement devient rectiligne uniforme.
On peut donc résumer par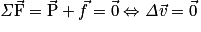 .
.
Avec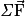 la somme vectorielle des forces qui s'exercent sur le système et
la somme vectorielle des forces qui s'exercent sur le système et 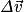 la variation du vecteur vitesse.
la variation du vecteur vitesse.
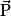 et la force de frottement
et la force de frottement 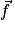 . Ces deux forces sont de même direction et de sens opposés. Si la force de frottement compense le poids, alors d'après le principe d'inertie la variation du vecteur vitesse du système est nulle, c'est-à-dire que le vecteur vitesse reste constant. Le mouvement devient rectiligne uniforme.
. Ces deux forces sont de même direction et de sens opposés. Si la force de frottement compense le poids, alors d'après le principe d'inertie la variation du vecteur vitesse du système est nulle, c'est-à-dire que le vecteur vitesse reste constant. Le mouvement devient rectiligne uniforme.On peut donc résumer par
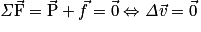 .
.Avec
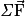 la somme vectorielle des forces qui s'exercent sur le système et
la somme vectorielle des forces qui s'exercent sur le système et 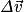 la variation du vecteur vitesse.
la variation du vecteur vitesse.• Exemple : Un parachutiste est soumis à son poids 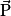 et à l'action de son parachute qui sera modélisée par une force
et à l'action de son parachute qui sera modélisée par une force 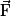 . Si ces deux forces se compensent, c'est-à-dire que
. Si ces deux forces se compensent, c'est-à-dire que 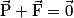 alors, d'après le principe d'inertie, la variation du vecteur vitesse est nulle c'est-à-dire que :
alors, d'après le principe d'inertie, la variation du vecteur vitesse est nulle c'est-à-dire que : 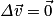 le vecteur vitesse reste constant. Avec le raisonnement réciproque, un parachutiste soumis à son poids
le vecteur vitesse reste constant. Avec le raisonnement réciproque, un parachutiste soumis à son poids 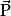 et à l'action de son parachute, qui sera modélisée par une force
et à l'action de son parachute, qui sera modélisée par une force 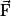 , tombe à vitesse constante. Donc, d'après le principe d'inertie, les forces appliquées sur lui se compensent c'est-à-dire
, tombe à vitesse constante. Donc, d'après le principe d'inertie, les forces appliquées sur lui se compensent c'est-à-dire 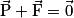 .
.
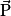 et à l'action de son parachute qui sera modélisée par une force
et à l'action de son parachute qui sera modélisée par une force 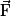 . Si ces deux forces se compensent, c'est-à-dire que
. Si ces deux forces se compensent, c'est-à-dire que 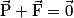 alors, d'après le principe d'inertie, la variation du vecteur vitesse est nulle c'est-à-dire que :
alors, d'après le principe d'inertie, la variation du vecteur vitesse est nulle c'est-à-dire que : 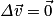 le vecteur vitesse reste constant. Avec le raisonnement réciproque, un parachutiste soumis à son poids
le vecteur vitesse reste constant. Avec le raisonnement réciproque, un parachutiste soumis à son poids 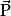 et à l'action de son parachute, qui sera modélisée par une force
et à l'action de son parachute, qui sera modélisée par une force 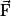 , tombe à vitesse constante. Donc, d'après le principe d'inertie, les forces appliquées sur lui se compensent c'est-à-dire
, tombe à vitesse constante. Donc, d'après le principe d'inertie, les forces appliquées sur lui se compensent c'est-à-dire 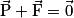 .
. À retenir :
Connaître le principe de l'inertie et savoir l'exploiter ou savoir exploiter sa contraposée pour en déduire des informations soit sur la nature du mouvement d'un système modélisé par un point matériel, soit sur les forces.
Savoir relier la variation entre deux instants voisins du vecteur vitesse d'un système modélisé par un point matériel à l'existence d'actions extérieures modélisées par des forces dont la somme est non nulle.
Savoir relier la variation entre deux instants voisins du vecteur vitesse d'un système modélisé par un point matériel dans le cas d'un mouvement de chute libre à une dimension au sens du vecteur poids exercé sur celui-ci.
Connaître le principe de l'inertie et savoir l'exploiter ou savoir exploiter sa contraposée pour en déduire des informations soit sur la nature du mouvement d'un système modélisé par un point matériel, soit sur les forces.
Savoir relier la variation entre deux instants voisins du vecteur vitesse d'un système modélisé par un point matériel à l'existence d'actions extérieures modélisées par des forces dont la somme est non nulle.
Savoir relier la variation entre deux instants voisins du vecteur vitesse d'un système modélisé par un point matériel dans le cas d'un mouvement de chute libre à une dimension au sens du vecteur poids exercé sur celui-ci.
© 2000-2026, Miscellane