Les configurations du plan
Fiche
Le théorème de Pythagore s'applique à un triangle rectangle ; le théorème de Thalès, à une figure qui comprend des droites parallèles coupées par deux sécantes. Pour conduire une démonstration dans un problème de géométrie plane, il faut savoir faire le lien entre une figure type et les propriétés qui lui sont associées.
1. Quelles propriétés peut-on utiliser dans un triangle rectangle ?
• Quand on veut mettre en relation les longueurs des côtés d'un triangle rectangle, on utilise le théorème de Pythagore qui s'énonce ainsi : dans un triangle rectangle, le carré de la longueur de l'hypoténuse est égal à la somme des carrés des longueurs des côtés de l'angle droit.
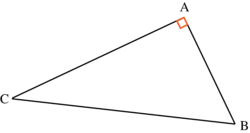 |
Par exemple, dans le triangle ABC rectangle en A, on a : 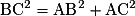 .
.
Réciproquement, si on veut montrer qu'un triangle ABC est rectangle en A, il suffit de montrer la relation sur les longueurs des côtés :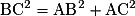 .
.
 .
.Réciproquement, si on veut montrer qu'un triangle ABC est rectangle en A, il suffit de montrer la relation sur les longueurs des côtés :
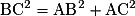 .
.• Quand on veut mettre en relation les angles et les longueurs des côtés d'un triangle rectangle, on a recours aux formules de trigonométrie :
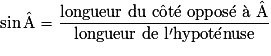
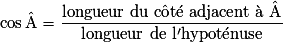
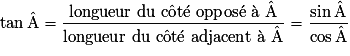
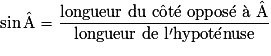
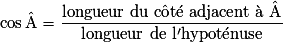
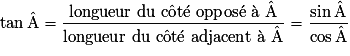
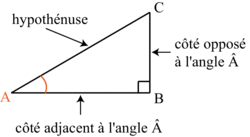 |
Il faut aussi connaître la relation 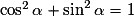 .
.
Démonstration : Pour tout réel x de [0;90], cos2(x) + sin2(x) = 1.
Soit un triangle ABC rectangle en A. Soit x une mesure en degrés de l'angle géométrique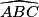 (saillant et aigu).
(saillant et aigu).
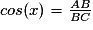 et
et 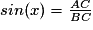 et BC2 = AB2 + AC2 (égalité de Pythagore).
et BC2 = AB2 + AC2 (égalité de Pythagore).
Ainsi :
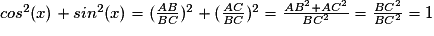
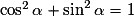 .
.Démonstration : Pour tout réel x de [0;90], cos2(x) + sin2(x) = 1.
Soit un triangle ABC rectangle en A. Soit x une mesure en degrés de l'angle géométrique
 (saillant et aigu).
(saillant et aigu).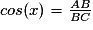 et
et 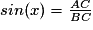 et BC2 = AB2 + AC2 (égalité de Pythagore).
et BC2 = AB2 + AC2 (égalité de Pythagore).Ainsi :
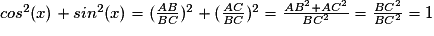
• Voici une dernière propriété à laquelle il faut penser quand on a affaire à un triangle rectangle inscrit dans un cercle :
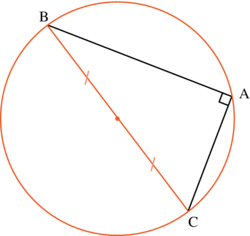 |
Dans un triangle rectangle, le centre du cercle circonscrit est le milieu de l'hypoténuse.
Réciproquement, si on veut montrer qu'un triangle est rectangle, il suffit de montrer qu'il s'inscrit dans un demi-cercle.
Exercice n°1Exercice n°2
Réciproquement, si on veut montrer qu'un triangle est rectangle, il suffit de montrer qu'il s'inscrit dans un demi-cercle.
Exercice n°1Exercice n°2
2. Quelles propriétés peut-on utiliser lorsque la figure comprend deux droites parallèles coupées par une sécante ?
• Sur la figure ci-dessous, les droites d et d' déterminent avec la sécante Δ :
– des couples d'angles correspondants, qui sont placés de la même façon par rapport aux droites, par exemple le couple d'angles marqués en bleu ;
– des couples d'angles alternes internes, qui sont placés de part et d'autre de la sécante et situés entre les parallèles, par exemple le couple d'angles marqués en orange ;
– des couples d'angles alternes externes, qui sont placés de part et d'autre de la sécante et à l'extérieur des parallèles, par exemple le couple d'angles marqués en vert.
– des couples d'angles correspondants, qui sont placés de la même façon par rapport aux droites, par exemple le couple d'angles marqués en bleu ;
– des couples d'angles alternes internes, qui sont placés de part et d'autre de la sécante et situés entre les parallèles, par exemple le couple d'angles marqués en orange ;
– des couples d'angles alternes externes, qui sont placés de part et d'autre de la sécante et à l'extérieur des parallèles, par exemple le couple d'angles marqués en vert.
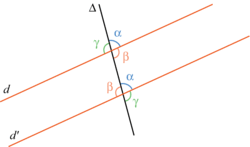 |
• Les droites d et d' étant parallèles, les angles de chacun de ces couples sont égaux entre eux. Ainsi les angles correspondants marqués en bleu ont pour même valeur α ; les angles alternes-internes marqués en orange ont pour même valeur β. les angles alternes-externes marqués en vert ont pour même valeur γ.
• Réciproquement, si deux droites d et d' et une sécante Δ déterminent des angles correspondants ou des angles alternes-internes ou des angles alternes-externes qui sont égaux, alors les droites d et d' sont parallèles.
Exercice n°3
Exercice n°3
3. Quelles propriétés peut-on utiliser lorsque la figure comprend deux droites parallèles coupées par deux droites sécantes ?
Voici deux figures types dans lesquelles on peut appliquer le théorème de Thalès énoncé ci-dessous.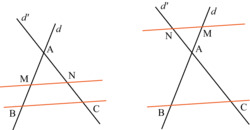 |
• Soit d et d' deux droites sécantes en A. On suppose que B et M sont deux points de d distincts de A et que C et N sont deux points de d' distincts de A.
Si les droites (BC) et (MN) sont parallèles, alors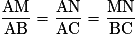 .
.
Si les droites (BC) et (MN) sont parallèles, alors
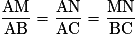 .
.• Réciproquement, si les points A, M, B sont alignés dans le même ordre que les points A, N, C et si 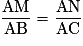 , alors les droites (BC) et (MN) sont parallèles.
, alors les droites (BC) et (MN) sont parallèles.
Exercice n°4
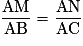 , alors les droites (BC) et (MN) sont parallèles.
, alors les droites (BC) et (MN) sont parallèles.Exercice n°4
4. Quelle propriété peut-on utiliser lorsque la figure comprend des angles inscrits dans un cercle ?
• Sur la figure ci-dessous, les angles 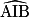 ,
, 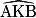 et
et  sont des angles inscrits dans le cercle de centre O car leur sommet est sur le cercle et leurs côtés coupent le cercle. Ils interceptent les arcs de cercle AB, passant par J pour les angles
sont des angles inscrits dans le cercle de centre O car leur sommet est sur le cercle et leurs côtés coupent le cercle. Ils interceptent les arcs de cercle AB, passant par J pour les angles 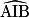 et
et 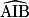 et passant par I pour l'angle
et passant par I pour l'angle  . L'angle
. L'angle 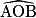 est appelé angle au centre.
est appelé angle au centre.
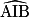 ,
, 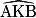 et
et  sont des angles inscrits dans le cercle de centre O car leur sommet est sur le cercle et leurs côtés coupent le cercle. Ils interceptent les arcs de cercle AB, passant par J pour les angles
sont des angles inscrits dans le cercle de centre O car leur sommet est sur le cercle et leurs côtés coupent le cercle. Ils interceptent les arcs de cercle AB, passant par J pour les angles 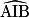 et
et 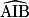 et passant par I pour l'angle
et passant par I pour l'angle  . L'angle
. L'angle 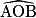 est appelé angle au centre.
est appelé angle au centre.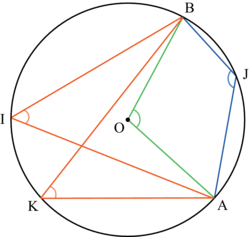 |
• On retiendra la propriété suivante : des angles inscrits dans le même cercle qui interceptent le même arc sont égaux, sur le dessin ce sont les angles 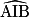 et
et 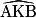 . De plus, leur mesure est la moitié de la mesure de l'angle au centre qui intercepte le même arc, sur le dessin, l'angle
. De plus, leur mesure est la moitié de la mesure de l'angle au centre qui intercepte le même arc, sur le dessin, l'angle 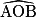 . Mais attention, les angles
. Mais attention, les angles 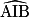 et
et  n'ont pas la même mesure (les deux angles n'interceptent pas le même arc AB).
n'ont pas la même mesure (les deux angles n'interceptent pas le même arc AB).
Exercice n°5Exercice n°6Exercice n°7Exercice n°8
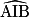 et
et 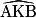 . De plus, leur mesure est la moitié de la mesure de l'angle au centre qui intercepte le même arc, sur le dessin, l'angle
. De plus, leur mesure est la moitié de la mesure de l'angle au centre qui intercepte le même arc, sur le dessin, l'angle 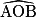 . Mais attention, les angles
. Mais attention, les angles 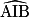 et
et  n'ont pas la même mesure (les deux angles n'interceptent pas le même arc AB).
n'ont pas la même mesure (les deux angles n'interceptent pas le même arc AB).Exercice n°5Exercice n°6Exercice n°7Exercice n°8
À retenir
• Le théorème de Pythagore énonce que, dans un triangle rectangle, le carré de la longueur de l'hypoténuse est égal à la somme des carrés des longueurs des côtés de l'angle droit.
• Des droites parallèles déterminent avec une sécante des angles correspondants égaux, des angles alternes internes égaux et des angles alternes externes égaux.
• D'après le théorème de Thalès, si d et d' sont deux droites sécantes en A, avec B et M deux points de d distincts de A et C et N, deux points de d' distincts de A, et si les droites (BC) et (MN) sont parallèles, alors 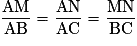 .
.
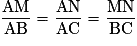 .
.• Des angles inscrits dans le même cercle qui interceptent le même arc sont égaux. De plus leur mesure est la moitié de la mesure de l'angle au centre qui intercepte le même arc.
© 2000-2026, Miscellane