Quand on connaît l'écriture d'une fonction, on peut préciser son ensemble de définition et déterminer son sens de variation. On complète ensuite un tableau de valeurs pour faire sa représentation graphique. Réciproquement, on peut partir de la représentation graphique d'une fonction pour trouver son ensemble de définition et déduire son tableau de variation. On peut également utiliser les représentations graphiques de fonctions pour résoudre des équations ou des inéquations.
1. Comment lire l'ensemble de définition sur la représentation graphique d'une fonction ?
Sur l'axe horizontal, on lit les abscisses des points de la courbe. L'ensemble de définition est l'ensemble de ces abscisses. Il s'écrit sous la forme d'un intervalle ou d'une réunion d'intervalles.
Exemple
La représentation graphique ci-dessous est formée de points dont l'abscisse est comprise entre −3 et 5, le nombre 1 étant exclu. Elle représente une fonction définie sur la réunion d'intervalles :![[ -3\,;\; 1[ \:\cup \: ]1\,;\; 5]](https://static1.assistancescolaire.com/2/images/2_m204_m1.png)
. |
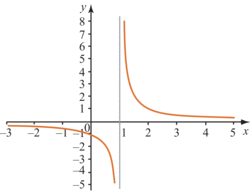2. Comment établir le tableau de variation d'une fonction à partir de sa représentation graphique ?
Une fonction est croissante sur un intervalle I, si, en parcourant la courbe de gauche à droite, les images en ordonnées augmentent.
Une fonction est décroissante sur un intervalle I, si, en parcourant la courbe de gauche à droite, les images en ordonnées diminuent.
Une fonction est constante sur un intervalle I lorsque sa représentation graphique est un segment horizontal.
Une fonction est décroissante sur un intervalle I, si, en parcourant la courbe de gauche à droite, les images en ordonnées diminuent.
Une fonction est constante sur un intervalle I lorsque sa représentation graphique est un segment horizontal.
Exemple
 |
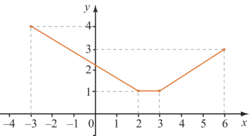La ligne brisée ci-dessus représente une fonction f :
– décroissante sur l'intervalle [-3 ; 2] ;
– constante sur l'intervalle [2 ; 3] ;
– croissante sur l'intervalle [3 ; 6].
– décroissante sur l'intervalle [-3 ; 2] ;
– constante sur l'intervalle [2 ; 3] ;
– croissante sur l'intervalle [3 ; 6].
Elle atteint son minimum 1 sur l'intervalle [2 ; 3].
On résume ces informations dans un tableau de variation :
On résume ces informations dans un tableau de variation :
 |
3. Comment lire les solutions d'une équation sur une représentation graphique de fonction(s) ?
• Les solutions de l'équation f(x) = k sont les abscisses des points d'intersection de la courbe représentant la fonction f avec la droite horizontale d'équation y = k.
Dans le cas particulier de l'équation f(x) = 0, les solutions sont les abscisses des points d'intersection de la courbe avec l'axe des abscisses.
Dans le cas particulier de l'équation f(x) = 0, les solutions sont les abscisses des points d'intersection de la courbe avec l'axe des abscisses.
Exemple
 |
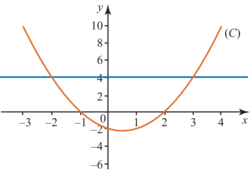La courbe (C) ci-dessus représente une fonction f.
L'ensemble des solutions de l'équation f(x) = 4 est : S = {−2 ; 3}.
L'ensemble des solutions de l'équation f(x) = 0 est : S = {−1 ; 2}.
L'ensemble des solutions de l'équation f(x) = 4 est : S = {−2 ; 3}.
L'ensemble des solutions de l'équation f(x) = 0 est : S = {−1 ; 2}.
• Les solutions de l'équation f(x) = g(x) sont les abscisses des points d'intersection de la courbe représentant f avec la courbe représentant g.
Exemple
La courbe (C) ci-dessus représente une fonction f et la droite (D) une fonction g. L'ensemble des solutions de l'équation f(x) = g(x) est : S = {0 ; 3}. |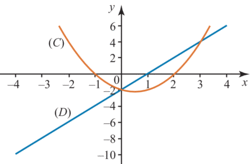
4. Comment lire les solutions d'une inéquation sur une représentation graphique de fonction(s) ?
• Les solutions de l'inéquation f(x) < k sont les abscisses des points de la courbe situés au-dessous de la droite d'équation y = k.
Dans le cas particulier de l'équation f(x) < 0, les solutions sont les abscisses des points de la courbe situés au-dessous de l'axe des abscisses.
Dans le cas particulier de l'équation f(x) < 0, les solutions sont les abscisses des points de la courbe situés au-dessous de l'axe des abscisses.
Exemple
 |
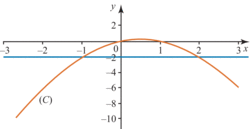La courbe (C) ci-dessus représente une fonction f.
L'ensemble des solutions de l'inéquation f(x) > −2 est :![S = ] - 1\,;\; 2[](https://static1.assistancescolaire.com/2/images/2_m204_m2.png)
.
L'ensemble des solutions de l'inéquation f(x) < 0 est :![S = ] - \infty\,;\; 0[ \: \cup \: ]1\,;\; + \infty [](https://static1.assistancescolaire.com/2/images/2_m204_m3.png)
.
L'ensemble des solutions de l'inéquation f(x) > −2 est :
.L'ensemble des solutions de l'inéquation f(x) < 0 est :
.• Plus généralement, les solutions de l'inéquation f(x) < g(x) sont les abscisses des points de la courbe représentant f, situés au-dessous de la courbe représentant g.
Exercice n°4
Exercice n°4
À retenir
• Pour déterminer l'ensemble de définition d'une fonction, on lit les abscisses des points de la représentation graphique. On l'écrit sous la forme d'un intervalle ou d'une réunion d'intervalles.
• Pour connaître le sens de variation sur un intervalle, on parcourt la courbe de gauche à droite et on observe si les ordonnées des points augmentent ou diminuent.
• Pour déterminer les solutions d'une équation de la forme f(x) = k, on lit les abscisses des points d'intersection de la courbe avec la droite horizontale d'équation y = k. Dans le cas d'une inéquation f(x) < k, on lit les abscisses des points de la courbe situés au-dessous de la droite d'équation y = k.
Exercice n°1
Soit le tableau de variation d'une fonction f :
 |
Son ensemble de définition est :
Cochez la bonne réponse.
| ||
| ||
|
![[ - 4\,;\; 0[ \: \cup\: ]0\,;\; 1]](https://static1.assistancescolaire.com/2/images/2_m204_m4.png)
![[ - 2\,;\; 6]](https://static1.assistancescolaire.com/2/images/2_m204_m5.png)
![[ - 2\,;\; 0[ \: \cup\: ]0\,;\; 6]](https://static1.assistancescolaire.com/2/images/2_m204_m6.png)
Le nombre 0 n'a pas d'image par la fonction f. Les valeurs de la variable x sont donc comprises entre −2 et 6, à l'exclusion de 0.
D'où son ensemble de définition :![D_f = [ - 2\,;\; 0[ \: \cup\: ]0\,;\; 6]](https://static1.assistancescolaire.com/2/images/2_m204_m7.png)
.
D'où son ensemble de définition :
.Exercice n°2
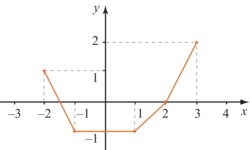
La ligne brisée représente une fonction f, définie sur l'intervalle [-2 ; 3] :
 |
Quel est la réponse fausse ?
Cochez la bonne réponse.
| ||
| ||
|
• L'image de -2, la borne inférieure de l'intervalle de définition, est 1. La borne supérieure 3 a une image plus grande : 2. Mais c'est insuffisant pour en conclure que f est croissante sur la totalité de l'intervalle [−2 ; 3]. La proposition « f est croissante sur [−2 ; 3] » est fausse.
• La fonction est strictement décroissante sur l'intervalle ![[- 2\,;\; -1]](https://static1.assistancescolaire.com/2/images/2_m204_m8.png)
et croissante au sens large sur l'intervalle [−1 ; 3].
et croissante au sens large sur l'intervalle [−1 ; 3].Exercice n°3
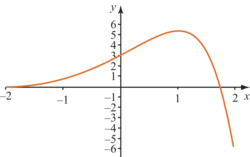
La courbe ci-dessous représente une fonction f, définie sur l'intervalle [−2 ; 3].
 |
Cochez la bonne réponse.
| ||
| ||
|
La solution de l'équation f(x) = 1 est l'abscisse du point d'intersection de la courbe représentant la fonction f avec la droite d'équation y = 1.
Exercice n°4
La courbe ci-dessous représente la variation du coût de fabrication, en euros, de x objets.
 |
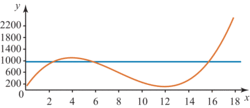Le coût de fabrication est inférieur à 1 000 € pour une production :
Cochez la bonne réponse.
| ||
| ||
|
Sur l'intervalle [6 ; 15], la courbe est entièrement au-dessous de la droite d'équation y = 1 000. Le coût de fabrication est alors inférieur à 1 000 €.
Pour 3, 4 ou 5 objets, le coût de fabrication est supérieur à 1 000 €.
Pour 3, 4 ou 5 objets, le coût de fabrication est supérieur à 1 000 €.
