C'est sous la Révolution française que s'impose l'usage, dans notre pays, du système métrique décimal. On voit alors apparaître l'expression pour cent qui au milieu du xixe siècle donne naissance au mot pourcentage.
La notion de pourcentage, utilisée aujourd'hui de manière quasi quotidienne dans la presse ou la publicité, est souvent mal maîtrisée et source d'erreurs. Précisons ici le calcul et l'usage des pourcentages.
La notion de pourcentage, utilisée aujourd'hui de manière quasi quotidienne dans la presse ou la publicité, est souvent mal maîtrisée et source d'erreurs. Précisons ici le calcul et l'usage des pourcentages.
1. Comment calculer un pourcentage ?
On définit d'abord E l'ensemble (ou la quantité) de référence, puis A la partie (ou la quantité) dont on calcule la proportion. On appelle, ici, n la grandeur de E et p la grandeur de A.Le pourcentage de A dans E (ou de A par rapport à E) est le nombre t tel que :
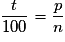 , soit
, soit 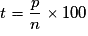 .
.Exemple
Sur une facture, on a les indications suivantes :Prix HT : 250 € − TVA : 45 € − Prix TTC : 295 €.
Quel est le taux de TVA appliqué ?
On cherche le pourcentage de 45 par rapport à 250.
La quantité de référence est le prix HT : 250.
La quantité dont on calcule la proportion est : 45.
Le pourcentage de TVA est donc :
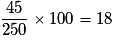 . Soit 18 %.
. Soit 18 %.Exercice n°1Exercice n°2
2. Comment utiliser un pourcentage ?
• Prendre t % d'un nombre x, c'est multiplier x par 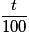 .
.
Ainsi, si un prix HT est de 330 € et que le taux de TVA est de 5,5 %, le montant de la TVA est « 5,5 % de 330 », c'est-à-dire :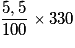 ; soit 18,15 €.
; soit 18,15 €.
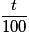 .
.Ainsi, si un prix HT est de 330 € et que le taux de TVA est de 5,5 %, le montant de la TVA est « 5,5 % de 330 », c'est-à-dire :
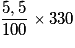 ; soit 18,15 €.
; soit 18,15 €.• Si le nombre y représente t % de x, on a 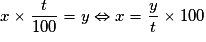 .
.
Prenons un exemple. La TVA sur un produit est de 6 % et s'élève à 27 €. Le prix hors taxe est le nombre x dont 6 % est égal à 27, c'est-à-dire le nombre x qui vérifie :
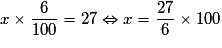 .
.
D'où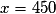 .
.
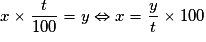 .
.Prenons un exemple. La TVA sur un produit est de 6 % et s'élève à 27 €. Le prix hors taxe est le nombre x dont 6 % est égal à 27, c'est-à-dire le nombre x qui vérifie :
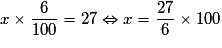 .
.D'où
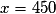 .
.• Pourcentage de pourcentage : prendre m % de t %, c'est prendre 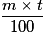 %.
%.
Exemple : dans un lycée, il y a 60 % de filles et parmi elles 30 % sont internes. Le pourcentage de filles internes dans le lycée est :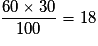 . Il y a donc 18 % de filles internes dans le lycée.
. Il y a donc 18 % de filles internes dans le lycée.
Exercice n°3Exercice n°4Exercice n°5Exercice n°6
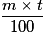 %.
%.Exemple : dans un lycée, il y a 60 % de filles et parmi elles 30 % sont internes. Le pourcentage de filles internes dans le lycée est :
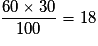 . Il y a donc 18 % de filles internes dans le lycée.
. Il y a donc 18 % de filles internes dans le lycée.Exercice n°3Exercice n°4Exercice n°5Exercice n°6
3. Comment calculer une augmentation ou une diminution de pourcentage ?
• Augmenter une quantité de t % équivaut à multiplier sa valeur initiale par 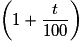 .
.
Ainsi, augmenter une quantité de 55 % équivaut à multiplier sa valeur initiale par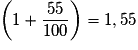 .
.
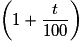 .
.Ainsi, augmenter une quantité de 55 % équivaut à multiplier sa valeur initiale par
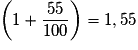 .
.• Diminuer une quantité de t % équivaut à multiplier sa valeur initiale par 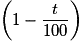 .
.
Ainsi, diminuer une quantité de 66 % équivaut à multiplier sa valeur initiale par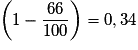 .
.
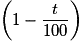 .
.Ainsi, diminuer une quantité de 66 % équivaut à multiplier sa valeur initiale par
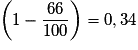 .
.Remarque
Considérer une augmentation ou une diminution en pourcentage comme une multiplication par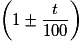 facilite la résolution de nombreux problèmes. Il faut être capable d'utiliser ce résultat dans les deux sens :
facilite la résolution de nombreux problèmes. Il faut être capable d'utiliser ce résultat dans les deux sens : - pour appliquer une augmentation ou une diminution (voir ci-dessus) ;
- pour déterminer un pourcentage d'augmentation ou de diminution.
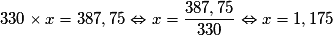 .
.Comme
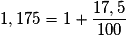 , on en déduit que le taux de TVA est de 17,5 %.
, on en déduit que le taux de TVA est de 17,5 %.Exercice n°7Exercice n°8Exercice n°9
4. Quel calcul effectuer dans le cas d'augmentations ou de diminutions successives ?
• Appliquer à une quantité une augmentation de t % puis de m % équivaut à multiplier sa valeur initiale par 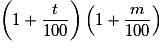 .
.
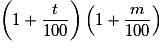 .
.• Appliquer à une quantité une diminution de t % puis de m % équivaut à multiplier sa valeur initiale par 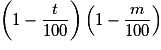 .
.
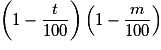 .
.• Appliquer à une quantité une augmentation de t % puis une diminution de m % équivaut à multiplier sa valeur initiale par 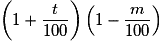 .
.
Exercice n°10Exercice n°11Exercice n°12
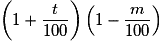 .
.Exercice n°10Exercice n°11Exercice n°12
5. Comment formuler des variations sous forme d'indices ?
On part d'une série chronologique :| Date | t0 | t1 | … | tk |
| Valeur | A0 | A1 | … | Ak |
L'indice
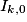 à la date tk, en prenant 100 pour base à la date t0 , est la quantité :
à la date tk, en prenant 100 pour base à la date t0 , est la quantité :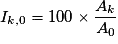 .
.Remarques
• L'indice est la quatrième proportionnelle dans le tableau de proportionnalité :
| 100 | Ik,0 |
| A0 | Ak |
• Les indices permettent non seulement de comparer plusieurs séries, mais aussi de déterminer rapidement des pourcentages d'évolution. Ainsi, le pourcentage d'évolution de A0 à Ak est : 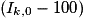 %.
%.
Exercice n°13Exercice n°14
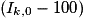 %.
%.Exercice n°13Exercice n°14
6. Evolution réciproque
Définition : L'évolution réciproque d'une évolution de la valeur V0 à V1 est l'évolution de la valeur V1 à V0.Propriété : L'évolution réciproque d'une évolution est une évolution de coefficient multiplicateur inverse.
Plus précisément, l'évolution réciproque d'une évolution de coefficient multiplicateur CM à pour coefficient multiplicateur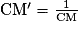
Plus précisément, l'évolution réciproque d'une évolution de coefficient multiplicateur CM à pour coefficient multiplicateur
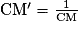
Remarque :
Soit V0 et V1 deux valeurs d'une même grandeur.
On définit deux évolutions réciproques : celle de V0 à V1 et celle de V1 à V0.
On désigne par t% le taux d'évolution de V0 à V1 et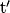 % celui deV1 à V0.
% celui deV1 à V0.
Ainsi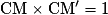
Soit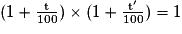
Soit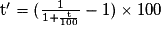
Exemple
Durant la journée de mardi, une action a augmenté de 7%.
Le mercredi soir, elle est revenue à son cours du mardi matin.
Calculer le taux d'évolution réciproque durant la journée du mercredi. Arrondir au dixième.
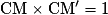
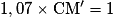
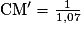
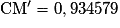 …
…
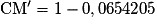 …
…
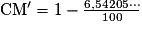
Durant la journée du mercredi, l'action a subi une baisse de 6,5% (arrondi au dixième).
Exercice n°15
Soit V0 et V1 deux valeurs d'une même grandeur.
On définit deux évolutions réciproques : celle de V0 à V1 et celle de V1 à V0.
On désigne par t% le taux d'évolution de V0 à V1 et
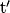 % celui deV1 à V0.
% celui deV1 à V0.Ainsi
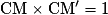
Soit
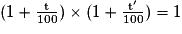
Soit
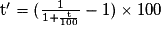
Exemple
Durant la journée de mardi, une action a augmenté de 7%.
Le mercredi soir, elle est revenue à son cours du mardi matin.
Calculer le taux d'évolution réciproque durant la journée du mercredi. Arrondir au dixième.
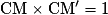
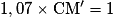
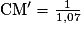
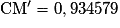 …
…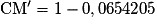 …
…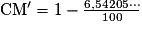
Durant la journée du mercredi, l'action a subi une baisse de 6,5% (arrondi au dixième).
Exercice n°15
À retenir
• Le pourcentage de A de grandeur p dans E de grandeur n est le nombre 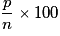 .
.
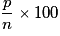 .
.• Augmenter une quantité de t % équivaut à multiplier sa valeur initiale par : 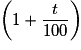 .
.
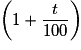 .
.• Diminuer une quantité de t % équivaut à multiplier sa valeur initiale par : 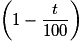 .
.
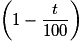 .
.• L'indice Ik,0 à la date tk, en prenant 100 pour base à la date t0, est la quantité :
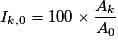 .
.
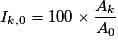 .
.Exercice n°1
Dans une boîte de M&M's, il y a 72 bonbons : 18 rouges, 13 verts, 12 bleus, 18 jaunes et 11 marrons. Le pourcentage de bonbons rouges dans la boîte est :
Cochez la bonne réponse.
| ||
| ||
|
La quantité de référence est : 72.
La quantité dont on calcule la proportion est : 18.
Le pourcentage de bonbons rouges dans la boîte est donc :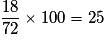 , soit 25 %.
, soit 25 %.
La quantité dont on calcule la proportion est : 18.
Le pourcentage de bonbons rouges dans la boîte est donc :
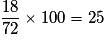 , soit 25 %.
, soit 25 %.Exercice n°2
Au printemps 2000, la population de lapins de la forêt de Rambouillet compte 12 500 individus. Pendant la période de reproduction, elle augmente de 630 %. Durant l'été et l'automne, sous l'action des prédateurs et des chasseurs, elle diminue de 74 %. Au début de l'hiver, le nombre de lapins de la forêt de Rambouillet est de :
Cochez la bonne réponse.
| ||
| ||
|
• Appliquer augmentation de 630 % revient à multiplier par 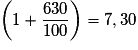 .
.
Or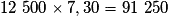 .
.
Il y a donc 91 250 lapins à la fin du printemps.
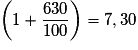 .
.Or
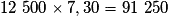 .
.Il y a donc 91 250 lapins à la fin du printemps.
• Appliquer une diminution de 74 % revient à multiplier par 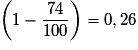 .
.
Or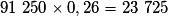 .
.
Il y a donc 23 725 lapins au début de l'hiver.
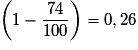 .
.Or
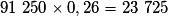 .
.Il y a donc 23 725 lapins au début de l'hiver.
Exercice n°3
Au printemps 2000, la population de lapins de la forêt de Rambouillet compte 12 500 individus. Pendant la période de reproduction, elle augmente de 630 %. Durant l'été et l'automne, sous l'action des prédateurs et des chasseurs, elle diminue de 74 %. Au final, la population a augmenté de :
Cochez la bonne réponse.
| ||
| ||
|
Une augmentation de 630 % revient à multiplier par 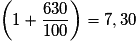 .
.
Une diminution de 74 % revient à multiplier par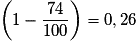 .
.
Au total, on a multiplié par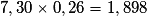 . Ce qui correspond à une augmentation de 89,8 %.
. Ce qui correspond à une augmentation de 89,8 %.
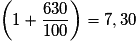 .
.Une diminution de 74 % revient à multiplier par
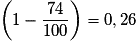 .
.Au total, on a multiplié par
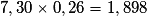 . Ce qui correspond à une augmentation de 89,8 %.
. Ce qui correspond à une augmentation de 89,8 %.Exercice n°4
Entendu à la radio lors des dernières élections municipales :
« Durant les 5 années qui viennent, nous diminuerons de 2 % chaque année les impôts locaux, ce qui nous donnera, sur 5 ans, une baisse de 10 %. » Cette conclusion est :
« Durant les 5 années qui viennent, nous diminuerons de 2 % chaque année les impôts locaux, ce qui nous donnera, sur 5 ans, une baisse de 10 %. » Cette conclusion est :
Cochez la bonne réponse.
| ||
| ||
|
Appliquer une diminution de 2 % revient à multiplier par 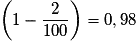 .
.
Appliquer cette diminution 5 années de suite revient à multiplier la quantité initiale par :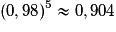 . Ce qui correspond à une baisse de 9,6 %
. Ce qui correspond à une baisse de 9,6 % 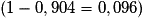 .
.
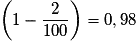 .
.Appliquer cette diminution 5 années de suite revient à multiplier la quantité initiale par :
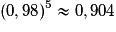 . Ce qui correspond à une baisse de 9,6 %
. Ce qui correspond à une baisse de 9,6 % 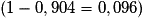 .
.Exercice n°5
Le tableau ci-dessous donne les montants, en milliers d'euros, du chiffre d'affaires d'une gamme de produits.
| Année | 1998 | 1999 | 2000 | 2001 |
| Chiffre d'affaires | 16,7 | 19,3 | 15,3 | 17,3 |
En prenant 100 pour base en 1998, l'indice (à 10-1 près) de l'année 2000 est :
Cochez la bonne réponse.
| ||
| ||
|
On a le tableau de proportionnalité suivant (où x est l'indice cherché) :
| 100 | x |
| 16,7 | 15,3 |
D'où :
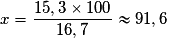 .
.L'indice cherché est donc : 91,6.
Exercice n°6
Le tableau ci-dessous donne les montants, en milliers d'euros, du chiffre d'affaires d'une gamme de produits.
| Année | 1998 | 1999 | 2000 | 2001 | 2002 |
| Chiffre d'affaires | 16,7 | 19,3 | 15,3 | 17,3 | … |
| Indice | 100 | 115,6 | 91,62 | 103,6 | 120 |
Si l'on prend 100 pour base en 1998, quel est le chiffre d'affaires manquant ?
Cochez la bonne réponse.
| ||
| ||
|
On a le tableau de proportionnalité suivant (où x est le chiffre d'affaires cherché) :
| 100 | 120 |
| 16,7 | x |
D'où :
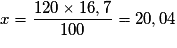 .
.Le chiffre d'affaires cherché est donc 20,04 milliers d'euros.
Exercice n°7
Le prix d'un produit dérivé du pétrole a augmenté de 60 % durant l'année 2005. Pour revenir à sa valeur initiale, ce prix doit baisser de :
Cochez la bonne réponse.
| ||
| ||
| ||
|
Augmenter une quantité de t % équivaut à multiplier sa valeur initiale par  .
.
Diminuer une quantité de t % équivaut à multiplier sa valeur initiale par .
.
Donc si p a été augmenté de 60 % puis baissé de t % alors le prix devient .
.
Si on veux retrouver le prix initial alors ce nouveau nombre doit être égal à p. On divise par p les deux membres (p différent de 0 car c'est un prix). On a alors . Puis on résout pour arriver à t = 37,5.
. Puis on résout pour arriver à t = 37,5.
 .
.Diminuer une quantité de t % équivaut à multiplier sa valeur initiale par
 .
.Donc si p a été augmenté de 60 % puis baissé de t % alors le prix devient
 .
. Si on veux retrouver le prix initial alors ce nouveau nombre doit être égal à p. On divise par p les deux membres (p différent de 0 car c'est un prix). On a alors
 . Puis on résout pour arriver à t = 37,5.
. Puis on résout pour arriver à t = 37,5. Exercice n°8
On a l'extrait de facture suivant :
Prix TTC : 1 300 €
Remise : 195 €
Dû : 1 105 €
On a bénéficié d'une remise de :
Prix TTC : 1 300 €
Remise : 195 €
Dû : 1 105 €
On a bénéficié d'une remise de :
Cochez la bonne réponse.
| ||
| ||
|
La quantité de référence est : 1 300.
La quantité dont on calcule la proportion est : 195.
D'où une remise de :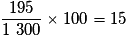 , soit 15 %.
, soit 15 %.
La quantité dont on calcule la proportion est : 195.
D'où une remise de :
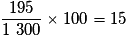 , soit 15 %.
, soit 15 %.Exercice n°9
Dans une entreprise de 350 personnes, il y a 40 % de femmes. Le nombre de femmes dans cette entreprise est de :
Cochez la bonne réponse.
| ||
| ||
|
Il s'agit de prendre 40 % des 350 personnes.
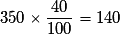 . Il y a donc 140 femmes dans l'entreprise.
. Il y a donc 140 femmes dans l'entreprise.
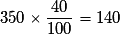 . Il y a donc 140 femmes dans l'entreprise.
. Il y a donc 140 femmes dans l'entreprise.Exercice n°10
Le loyer de M. Durand est de 258 € et représente 24 % de son revenu mensuel. Le revenu mensuel de M. Durand est de :
Cochez la bonne réponse.
| ||
| ||
|
Il s'agit de déterminer le nombre x tel que : 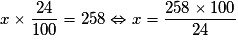 .
.
On obtient x = 1 075 €.
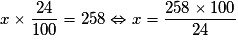 .
.On obtient x = 1 075 €.
Exercice n°11
Dans une entreprise de 350 personnes, il y a 40 % de femmes dont 25 % sont mariées. Le pourcentage de femmes mariées dans l'entreprise est de :
Cochez la bonne réponse.
| ||
| ||
|
Il s'agit de calculer un pourcentage de pourcentage.
Le pourcentage de femmes mariées dans l'entreprise est de :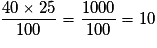 , soit 10 %.
, soit 10 %.
Le pourcentage de femmes mariées dans l'entreprise est de :
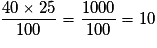 , soit 10 %.
, soit 10 %.Exercice n°12
Dans une entreprise de 350 personnes, il y a 60 % d'hommes dont 30 % sont mariés. Le nombre d'hommes mariés dans l'entreprise est de :
Cochez la bonne réponse.
| ||
| ||
|
Le pourcentage d'hommes mariés dans l'entreprise est de : 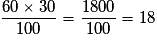 , soit 18 %.
, soit 18 %.
18 % de 350 donne :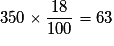 .
.
Il y a 63 hommes mariés dans cette entreprise.
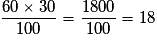 , soit 18 %.
, soit 18 %.18 % de 350 donne :
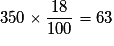 .
.Il y a 63 hommes mariés dans cette entreprise.
Exercice n°13
La population de Bourg-sur-Brie était de 3 550 habitants en 1990. Elle a augmenté de 12 % en 10 ans. En 2000, le nombre d'habitants de Bourg-sur-Brie est de :
Cochez la bonne réponse.
| ||
| ||
|
Appliquer une augmentation de 12 % revient à multiplier par : 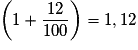 .
.
Or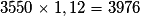 .
.
En 2000, le nombre d'habitants de Bourg-sur-Brie est donc 3 976.
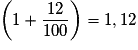 .
.Or
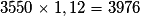 .
.En 2000, le nombre d'habitants de Bourg-sur-Brie est donc 3 976.
Exercice n°14
Suite à l'augmentation de sa population, le maire de Bourg-sur-Brie décide d'une baisse de 7 % des impôts locaux. Si M. Durand payait 170 €, après la baisse, il paiera :
Cochez la bonne réponse.
| ||
| ||
|
Appliquer une diminution de 7 % revient à multiplier par 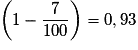 .
.
Or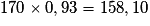 .
.
M. Durand paiera donc 158,10 €.
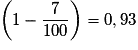 .
.Or
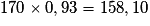 .
.M. Durand paiera donc 158,10 €.
Exercice n°15
Au printemps, la population de lapins de la forêt de Rambouillet, qui, avant les premiers soleils, était de 12 500 individus, augmente de 630 %. Elle compte alors :
Cochez la bonne réponse.
| ||
| ||
|
Appliquer une augmentation de 630 % revient à multiplier par 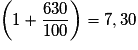 .
.
Or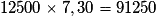 .
.
Il y a donc 91 250 lapins à la fin du printemps.
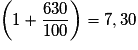 .
.Or
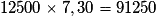 .
.Il y a donc 91 250 lapins à la fin du printemps.

