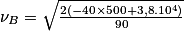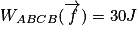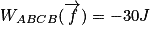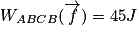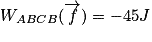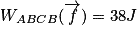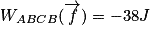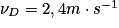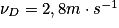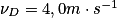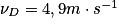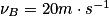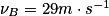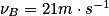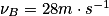Dans La Science et l'Hypothèse (1902), Henri Poincaré écrit : « Dans ce cas simple (système isolé formé d'un certain nombre de points matériels), l'énoncé du principe de la conservation de l'énergie est d'une extrême simplicité. » Plus loin, pour des systèmes complexes, il ajoute, de manière provocatrice « parmi les fonctions qui demeurent constantes… comment choisir celle qui doit s'appeler l'énergie ? Nous n'avons plus rien qui puisse nous guider dans notre choix. Il ne nous reste plus qu'un énoncé pour le principe de la conservation de l'énergie ». Et, il ajoute un peu plus loin « personne n'ignore que la conservation de l'énergie est un fait expérimental ».
I. Travail d'une force
Notion de travail d'une force
• Un solide soumis à une force dont le point d'application se déplace peut :
- être mis en mouvement (exemple : shoot dans un ballon de foot) ;
- changer d'altitude (exemple : bille qui tombe) ;
- se déformer temporairement ou définitivement (exemples : les oscillations d'un ressort ou une voiture lors d'un accident) ;
- voir sa température s'élever (exemple : disques de frein lors d'un freinage).
• Dans tous ces cas, on dit que la force fournit un travail.
Travail d'une force constante
• Une force est dite conservative si le travail de cette force est indépendant du chemin suivi. Si ce n'est pas le cas, elle est alors dite non conservative.
• Le travail d'une force constante 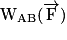 est égal au produit scalaire de la force
est égal au produit scalaire de la force 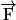 par la longueur
par la longueur 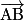 :
:
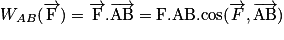 .
.
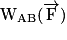 est égal au produit scalaire de la force
est égal au produit scalaire de la force 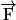 par la longueur
par la longueur 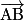 :
: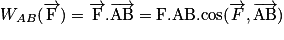 .
.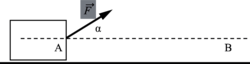 |
• Le travail peut être négatif (travail résistant) ou positif (travail moteur).
Différents cas particuliers :
Différents cas particuliers :
• La force 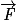 est perpendiculaire au déplacement :
est perpendiculaire au déplacement :
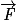 est perpendiculaire au déplacement :
est perpendiculaire au déplacement :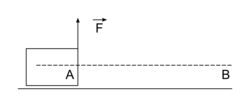 |
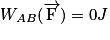
• La force 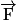 a la même direction et le même sens que le déplacement :
a la même direction et le même sens que le déplacement :
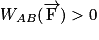
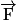 a la même direction et le même sens que le déplacement :
a la même direction et le même sens que le déplacement :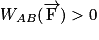
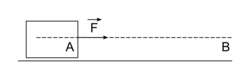 |
Le travail de 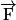 favorise le déplacement de A vers B, on dit
favorise le déplacement de A vers B, on dit 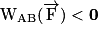 que le travail est moteur.
que le travail est moteur.
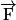 favorise le déplacement de A vers B, on dit
favorise le déplacement de A vers B, on dit 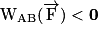 que le travail est moteur.
que le travail est moteur.• La force 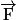 a la même direction que le déplacement, mais un sens opposé :
a la même direction que le déplacement, mais un sens opposé :
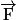 a la même direction que le déplacement, mais un sens opposé :
a la même direction que le déplacement, mais un sens opposé :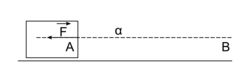 |
Le travail de 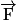 ne favorise pas le déplacement de l'objet de A vers B, on dit que le travail est résistant.
ne favorise pas le déplacement de l'objet de A vers B, on dit que le travail est résistant.
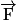 ne favorise pas le déplacement de l'objet de A vers B, on dit que le travail est résistant.
ne favorise pas le déplacement de l'objet de A vers B, on dit que le travail est résistant.Travail du poids
• Si l'on reste assez proche de la surface de la Terre, le poids d'un corps peut être considéré comme une force constante. Le travail du poids, au cours d'un déplacement du centre de gravité G, d'une position A vers une position B s'écrit :
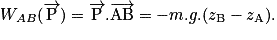
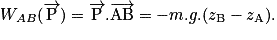
• Le travail du poids est indépendant du chemin parcouru. C'est une force conservative. Il ne dépend que de la différence d'altitude entre les points d'arrivée zB et de départ zA de G.
• Le travail du poids est positif si m descend (travail moteur) et il est négatif si m monte (travail résistant).
Travail d'une force non conservative : travail des forces de frottement au cours d'une trajectoire rectiligne
• Les forces de frottements 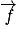 , supposées constantes, sont en sens opposé du mouvement :
, supposées constantes, sont en sens opposé du mouvement :
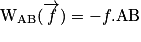
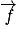 , supposées constantes, sont en sens opposé du mouvement :
, supposées constantes, sont en sens opposé du mouvement :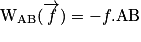
• Avec AB la longueur du chemin suivi. Ici le travail dépend du chemin suivi entre l'état initial et l'état final. On dit que 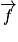 n'est pas conservative. Le travail des forces de frottement est résistant.
n'est pas conservative. Le travail des forces de frottement est résistant.
Exercice n°1
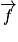 n'est pas conservative. Le travail des forces de frottement est résistant.
n'est pas conservative. Le travail des forces de frottement est résistant.Exercice n°1
II. Travail et énergie cinétique
Énergie cinétique
• Un solide de masse m en mouvement de translation (tous les points sont animés du même vecteur vitesse 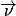 ) à la vitesse v possède l'énergie cinétique :
) à la vitesse v possède l'énergie cinétique :
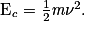
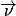 ) à la vitesse v possède l'énergie cinétique :
) à la vitesse v possède l'énergie cinétique :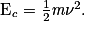
• Ec est en joule (J), m est en kilogramme (kg), ν est en mètre par seconde 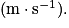
Théorème de l'énergie cinétique
Dans un référentiel galiléen, la variation de l'énergie cinétique d'un solide, entre deux instants tinitial (position A) et tfinal (position B), est égale à la somme des travaux des forces extérieures appliquées au solide entre ces deux instants.
• Pour un solide en translation soumis aux forces 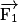 ,
, 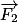 …, on peut écrire :
…, on peut écrire :
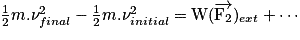
soit :
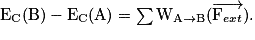
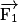 ,
, 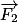 …, on peut écrire :
…, on peut écrire :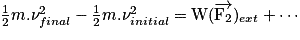
soit :
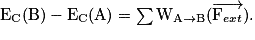
III. Travail et énergie potentielle de pesanteur
Le travail du poids
• Le travail du poids, au cours d'un déplacement du centre de gravité G, d'une position A vers une position B s'écrit :
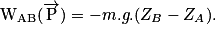
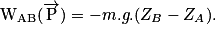
• Le poids est une force conservative, on dit qu'il dérive d'une énergie potentielle :
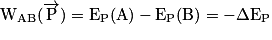 ,
,
en posant :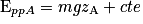 et
et 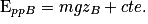
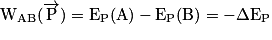 ,
,en posant :
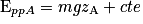 et
et 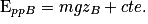
• Cette constante représente la valeur de l'énergie potentielle de pesanteur à l'altitude z = 0 m. Pour simplifier, on prend par convention cte = 0 J pour z = 0 m.
• Cette relation signifie que la variation d'énergie potentielle de pesanteur est le travail qu'il faut fournir pour éloigner un corps du centre de la Terre d'un point A à un point B, le corps étant au repos en A et en B.
Énergie potentielle de pesanteur
• On appelle énergie potentielle de pesanteur, notée Ep, la grandeur définie par :
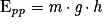
où h est l'altitude en m.
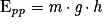
où h est l'altitude en m.
IV. Énergie mécanique et frottements
L'énergie mécanique
On définit l'énergie mécanique comme la somme de l'énergie cinétique et de l'énergie potentielle :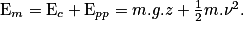
Conservation de l'énergie mécanique
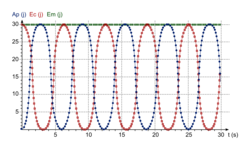
• Lorsque le système n'est soumis qu'à des forces conservatives, l'énergie mécanique est constante (se conserve), c'est-à-dire que la variation d'énergie mécanique est nulle. On a alors :
ΔEm = 0.
ΔEm = 0.
• Exemple : un pendule de masse m est mis en mouvement. On suppose que les forces de frottement sont négligeables. Lorsque l'énergie mécanique se conserve, si l'énergie cinétique augmente, alors l'énergie potentielle diminue. Il y a transformation d'énergie potentielle en énergie cinétique ou inversement.
 |
Non-conservation de l'énergie mécanique
• En revanche, lorsque l'on ne peut plus négliger les forces de frottement, la variation de l'énergie mécanique ΔEm est négative (diminution), de même que la somme des travaux résistants des forces de frottement.
• Exemple : un pendule de masse m est mis en mouvement.
 |
• Dans ce cas précis, l'énergie mécanique ne se conserve plus, elle diminue au cours du mouvement : l'échange entre l'énergie potentielle de pesanteur et l'énergie cinétique n'est plus réciproque, l'énergie potentielle de pesanteur diminue beaucoup plus vite que l'énergie cinétique n'augmente.
• Par conséquent, lorsque le système est soumis au moins à une force non conservative, son énergie mécanique ne se conserve pas, la variation d'énergie mécanique est égale à la somme des travaux des forces non conservatives (forces de frottement). On a alors :

Exercice n°2Exercice n°3Exercice n°4

Exercice n°2Exercice n°3Exercice n°4
À savoir et savoir réaliser :
- Connaître l'énergie cinétique d'un système modélisé par un point matériel.
- Utiliser l'expression de l'énergie cinétique d'un système modélisé par un point matériel.
- Connaître ce qu'est le travail d'une force et l'expression du travail dans le cas d'une force constante.
- Utiliser l'expression du travail
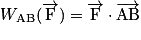 dans le cas de forces constantes.
dans le cas de forces constantes. - Énoncer et exploiter le théorème de l'énergie cinétique.
- Connaître ce qu'est une force conservative.
- Établir et utiliser l'expression de l'énergie potentielle de pesanteur pour un système au voisinage de la surface de la Terre.
- Connaître ce qu'est une force non-conservative.
- Calculer le travail d'une force de frottement d'intensité constante dans le cas d'une trajectoire rectiligne.
- Connaître ce qu'est l'énergie mécanique.
- Identifier des situations de conservation et de non-conservation de l'énergie mécanique.
- Exploiter la conservation de l'énergie mécanique dans des cas simples : chute libre en l'absence de frottement, oscillations d'un pendule en l'absence de frottement, etc.
- Utiliser la variation de l'énergie mécanique pour déterminer le travail des forces non conservatives.
Exercice n°1
Un palet de hockey glisse sur une patinoire glacée. Il finit par s'arrêter en raison de l'action mécanique de la glace, due à la force de frottement.
Cochez la bonne réponse.
| ||
| ||
| ||
| ||
| ||
|
Que vaut le travail de la force de frottement lors du déplacement du palet de A à B en faisant un rebond en C ?
Données : f = 5,0 N ; AB = 6,0 m et BC, = 1,5 m.
Données : f = 5,0 N ; AB = 6,0 m et BC, = 1,5 m.
Cochez la bonne réponse.
| ||
| ||
| ||
| ||
| ||
|
Le travail de la force de frottement pour aller de A à B est donné par 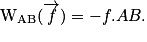
Par un raisonnement analogue, on trouve que le travail de la force de frottement pour aller de B à C est donné par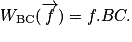
De même, on aura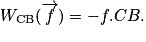
Pour pouvoir calculer le travail demandé, il faut additionner toutes les valeurs précédentes. L'erreur qu'il ne faut pas commettre est de penser que le travail de B vers C compense celui de C vers B, alors que la force de frottement s'inverse en C puisqu'elle est toujours opposée au mouvement. Ces deux travaux ne s'annulent pas puisqu'ils ont le même signe.
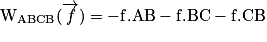 ,
,
soit numériquement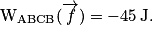
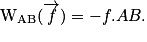
Par un raisonnement analogue, on trouve que le travail de la force de frottement pour aller de B à C est donné par
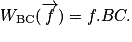
De même, on aura
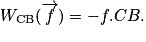
Pour pouvoir calculer le travail demandé, il faut additionner toutes les valeurs précédentes. L'erreur qu'il ne faut pas commettre est de penser que le travail de B vers C compense celui de C vers B, alors que la force de frottement s'inverse en C puisqu'elle est toujours opposée au mouvement. Ces deux travaux ne s'annulent pas puisqu'ils ont le même signe.
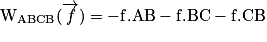 ,
,soit numériquement
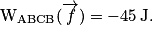
Exercice n°2
Un skateur part du point A sans aucune vitesse initiale. Pour modéliser la situation, on assimile le skateur à un point matériel en mouvement dans le champ de pesanteur uniforme. On néglige tous les frottements au cours du mouvement.
Que vaut sa vitesse au point D ?
Que vaut sa vitesse au point D ?
 |
Cochez la bonne réponse.
| ||
| ||
| ||
|
Données : la masse du skateur + skate m = 70 kg, ZA = 2,0 m ; ZB = 0,50 m ; ZC = 1,2 m et ZD = 0,80 m ; 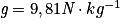 .
.
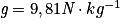 .
. Cochez la bonne réponse.
| ||
| ||
| ||
|
On calcule l'énergie mécanique au point A :
Em(A) = Epp(A) + Ec(A)
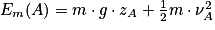
Comme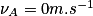 , alors
, alors 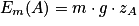 .
.
Comme il n'y a pas de frottement, l'énergie mécanique se conserve entre A et D.
D'où Em(A) = Em(D).
Or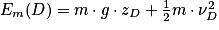 ,
,
soit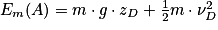 ,
,
d'où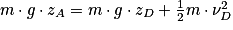
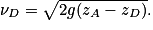
Soit numériquement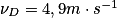
Em(A) = Epp(A) + Ec(A)
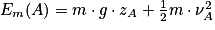
Comme
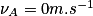 , alors
, alors 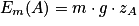 .
.Comme il n'y a pas de frottement, l'énergie mécanique se conserve entre A et D.
D'où Em(A) = Em(D).
Or
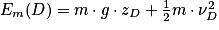 ,
,soit
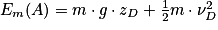 ,
,d'où
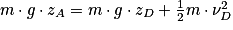
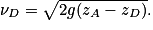
Soit numériquement
Exercice n°3
Parmi les affirmations suivantes, laquelle est correcte ?
Cochez la bonne réponse.
| ||
|
L'énergie cinétique est maximale lorsque l'énergie potentielle est minimale et inversement l'énergie potentielle est maximale lorsque l'énergie cinétique est minimale.
Exercice n°4
Un skieur de masse m = 90 kg dévale une piste, inclinée d'un angle α = 5,0° avec l'horizontale, depuis le point A jusqu'au point B. Sa vitesse initiale est nulle en A. On suppose que tout le long de la piste, une force de frottement f opposée au mouvement s'applique sur le skieur. La valeur de la force de frottement est f = 40 N.
Cochez la (ou les) bonne(s) réponse(s).
| ||
| ||
| ||
|
Quelle est la vitesse du skieur au point B ?
Données :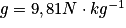 ; AB = 500 m.
; AB = 500 m.
Données :
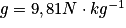 ; AB = 500 m.
; AB = 500 m. Cochez la (ou les) bonne(s) réponse(s).
| ||
| ||
| ||
|
L'énergie mécanique au point A est 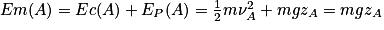 , car la vitesse initiale au point A est nulle.
, car la vitesse initiale au point A est nulle.
Pour calculer la hauteur du point A :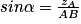 , soit
, soit 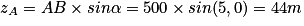
Em(A) = 90 × 9,81 × 44 = 3,8.104 J.
L'énergie mécanique au point B est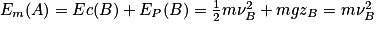 , car l'altitude au point B est nulle.
, car l'altitude au point B est nulle.
Il y a des forces de frottement qui sont des forces non conservatives et qui s'exercent sur le skieur, ainsi on peut écrire :
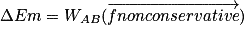 ,
,
Soit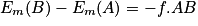 ,
,
d'où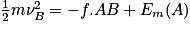 ,
,
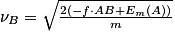
Numériquement,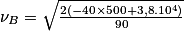
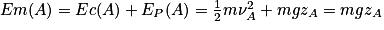 , car la vitesse initiale au point A est nulle.
, car la vitesse initiale au point A est nulle.Pour calculer la hauteur du point A :
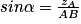 , soit
, soit 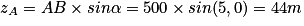
Em(A) = 90 × 9,81 × 44 = 3,8.104 J.
L'énergie mécanique au point B est
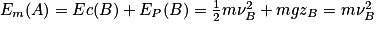 , car l'altitude au point B est nulle.
, car l'altitude au point B est nulle. Il y a des forces de frottement qui sont des forces non conservatives et qui s'exercent sur le skieur, ainsi on peut écrire :
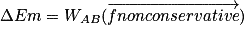 ,
,Soit
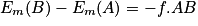 ,
,d'où
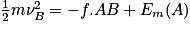 ,
,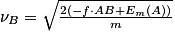
Numériquement,