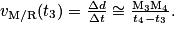Mouvement d'un système
Fiche
La formulation du premier principe, le principe d'inertie, représente le verrou qu'il fallait faire sauter pour que les autres lois de la mécanique puissent émerger, et avec elle, la science moderne. L'élaboration de ce principe, à laquelle les noms de Bruno, Galilée, Descartes et Newton sont notamment associés, prendra quasiment un siècle. Les progrès ultérieurs seront beaucoup plus rapides. Et ainsi, partant d'une situation de repos, la mise en mouvement nécessite une action : mais que sont ces interactions ?
I. Rappels
Solide ou système mécanique
Quantité de matière constante au cours du temps. On choisit librement le système qu'on étudie. Tout ce qui n'est pas le système étudié est appelé l'extérieur.Solide indéformable
L'expérience montre que la forme de certains solides ne dépend pas des actions que l'on exerce sur eux.Solide déformable
Ce sont des systèmes mécaniques mous, élastiques, liquides ou un ensemble de solides non rigidement liés.Translation
On choisit un segment joignant deux points quelconques d'un solide. Dans un solide en translation, ce segment reste parallèle à lui-même au cours du mouvement. La translation peut être rectiligne, circulaire ou curviligne.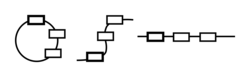 |
Rotation autour d'un axe
Dans un tel mouvement, il existe, dans le solide, un axe imaginaire dont les points restent fixes. Tous les autres points sont animés d'un mouvement circulaire centré sur cet axe.Référentiel
C'est un observateur muni d'un moyen pour mesurer le temps. Un système d'axes de coordonnées peut être lié à cet observateur.Repère
• C'est un système d'axes muni d'une base et d'une origine.
• Exemple :
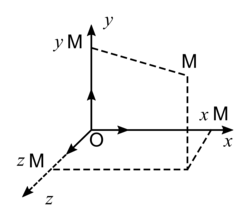 |
- O origine du repère ;
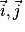 et
et 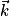 les vecteurs de base ;
les vecteurs de base ;- Ox, Oy et Oz les axes de coordonnées ;
- xM, yM et zM les coordonnées du point M ou les composantes du vecteur
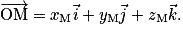
Trajectoire
Un point est en mouvement par rapport à un référentiel auquel est attaché un repère. La courbe décrite, dans le temps, par ce point est appelée sa trajectoire dans le référentiel considéré.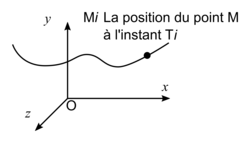 |
Vecteur vitesse instantanée d'un point du solide
• La vitesse d'un point d'un solide est la distance parcourue par ce point divisé par le temps mis par ce point pour parcourir cette distance. Cette vitesse sera moyenne si elle est mesurée sur une distance et instantanée si elle est mesurée en un point de la trajectoire.
• La vitesse instantanée d'un point d'un solide par rapport au référentiel (R) est sa vitesse à l'instant t. On la note 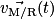 (ou
(ou 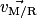 ou
ou 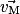 suivant le problème). Ce vecteur a les caractéristiques suivantes :
suivant le problème). Ce vecteur a les caractéristiques suivantes :
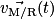 (ou
(ou 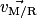 ou
ou 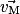 suivant le problème). Ce vecteur a les caractéristiques suivantes :
suivant le problème). Ce vecteur a les caractéristiques suivantes :- direction : selon la tangente à la trajectoire au point occupé par M à la date t ;
- sens : celui du mouvement à cet instant ;
- norme : la valeur positive
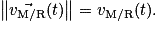
• Le point M parcourt une distance Δd extrêmement petite. Δt est le temps extrêmement petit mis par M pour parcourir Δd. On a : 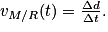
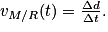
• Exemple :
 |
II. Première loi de Newton : principe d'inertie
Référentiels galiléens
• En cherchant à vérifier expérimentalement le principe de l'inertie, on arrive à la conclusion que le référentiel héliocentrique est galiléen et qu'il existe une infinité de référentiels galiléens, tous animés par rapport au référentiel héliocentrique d'un mouvement de translation rectiligne uniforme.
• Les référentiels terrestre et géocentrique ne sont pas galiléens puisque la Terre tourne autour du Soleil. Néanmoins, pour la plupart des applications pratiques qui ne réclament pas une extrême précision, l'expérience montre qu'ils peuvent être considérés comme galiléens.
Solide pseudo-isolé
La somme vectorielle des forces qui sont appliquées au solide est nulle.Système isolé
Il ne s'exerce aucune force sur le solide.Principe du centre d'inertie ou première loi de Newton
• Lorsque les forces qui s'exercent sur un solide se compensent, son centre d'inertie persévère en son état de repos ou de mouvement rectiligne.
• Réciproquement, si le centre d'inertie d'un solide isolé ou pseudo-isolé persévère en son état de repos ou de mouvement rectiligne uniforme, les forces qui s'exercent sur lui se compensent.
• On a les relations mathématiques suivantes :
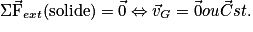
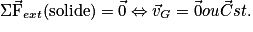
• Le principe du centre d'inertie ne concerne que le centre d'inertie du système, ce qui n'exclut pas la rotation éventuelle du système autour de son centre d'inertie.
• Par rapport à certains référentiels :
- si la vitesse du centre d'inertie d'un système est un vecteur constant, alors la somme des forces qui s'exercent sur le système est nulle ;
- si la somme des forces qui s'exercent sur un système est nulle, alors la vitesse du centre d'inertie du système est un vecteur constant.
• Les référentiels dans lesquels le principe du centre d'inertie est vérifié sont alors dits galiléens.
• Pour la plupart des situations que nous étudierons, la Terre pourra être considérée comme un référentiel galiléen.
III. Deuxième loi de Newton
Deuxième loi de Newton : aspect semi-quantitatif
• Dans un référentiel galiléen :
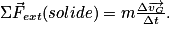
- si le vecteur vitesse du centre d'inertie varie, la somme des forces qui s'exercent sur le solide n'est pas nulle ;
- la variation, entre deux instants, du vecteur vitesse et la résultante des forces, appliquées entre ces deux instants, ont la même direction et le même sens ;
- si on appelle
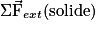 , la résultante de forces appliquée au solide de masse m, et
, la résultante de forces appliquée au solide de masse m, et 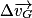 la variation de vitesse du centre d'inertie pendant la durée Δt, on a alors :
la variation de vitesse du centre d'inertie pendant la durée Δt, on a alors :
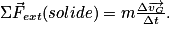
• La variation de la vitesse 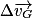 du centre d'inertie calculée sur un intervalle de temps de faible durée et la somme des forces
du centre d'inertie calculée sur un intervalle de temps de faible durée et la somme des forces 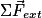 qui s'exercent sur le système pendant cet intervalle sont proportionnelles.
qui s'exercent sur le système pendant cet intervalle sont proportionnelles.
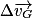 du centre d'inertie calculée sur un intervalle de temps de faible durée et la somme des forces
du centre d'inertie calculée sur un intervalle de temps de faible durée et la somme des forces 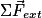 qui s'exercent sur le système pendant cet intervalle sont proportionnelles.
qui s'exercent sur le système pendant cet intervalle sont proportionnelles.Deuxième loi de Newton : méthode de construction du vecteur variation de vitesse
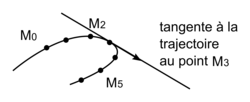
• On cherche à construire le vecteur variation de vitesse 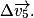
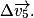
- 1re étape : tracer le segment entre les points 4 et 5 ;
- 2e étape : calculer
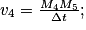
- 3e étape : grâce à une échelle bien choisie, tracer le vecteur vitesse
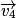 qui a pour origine le point M4 et qui est tangent à la trajectoire ;
qui a pour origine le point M4 et qui est tangent à la trajectoire ; - 4e étape : faire de même avec le vecteur vitesse
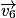 ;
; - 5e étape : reporter le vecteur vitesse
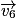 au point M5 ;
au point M5 ; - 6e étape : reporter le vecteur vitesse
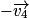 au bout du vecteur vitesse
au bout du vecteur vitesse 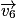 ;
; - 7e étape : le vecteur
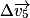 est le vecteur qui joint l'origine du vecteur
est le vecteur qui joint l'origine du vecteur 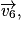 au point M5, à l'extrémité du vecteur
au point M5, à l'extrémité du vecteur 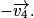
 |
IV. Troisième loi de Newton : principe des actions réciproques
• Avec deux dynamomètres A et B, on observe les forces suivantes :
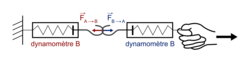 |
• Les indications des dynamomètres A et B sont identiques.
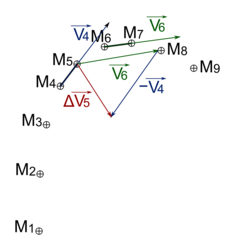
• Lorsqu'un corps A exerce sur un corps B une action mécanique modélisée par la force 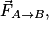 alors le corps B exerce sur le corps A l'action mécanique modélisée par la force
alors le corps B exerce sur le corps A l'action mécanique modélisée par la force 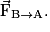 Les forces
Les forces 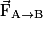 et
et 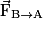 ont même intensité, même direction et des sens contraires :
ont même intensité, même direction et des sens contraires :
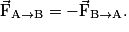
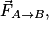 alors le corps B exerce sur le corps A l'action mécanique modélisée par la force
alors le corps B exerce sur le corps A l'action mécanique modélisée par la force 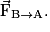 Les forces
Les forces 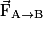 et
et 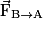 ont même intensité, même direction et des sens contraires :
ont même intensité, même direction et des sens contraires :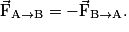
• Ce résultat s'applique à toute interaction entre deux systèmes, qu'ils soient en mouvement ou immobiles, qu'ils soient en contact ou non.
Exercice n°3Exercice n°4
Exercice n°3Exercice n°4
À savoir et savoir réaliser :
- Connaître la définition du vecteur variation de vitesse.
- Utiliser la relation approchée entre la variation du vecteur vitesse d'un système modélisé par un point matériel entre deux instants voisins et la somme des forces appliquées sur celui-ci : pour en déduire une estimation de la variation de vitesse entre deux instants voisins, les forces appliquées au système étant connues ; pour en déduire une estimation des forces appliquées au système, le comportement cinématique étant connu.
- Comprendre le rôle de la masse dans la relation entre la variation du vecteur vitesse d'un système entre deux instants et la somme des forces appliquées sur celui-ci.
© 2000-2026, Miscellane