Refroidissement d'un fer à cheval, sujet de métropole, mai 2022, exercice au choix B
Énoncé
Exercice sur 5 points
Mots-clés : premier principe de la thermodynamique, loi de Newton de la thermique
Le maréchal-ferrant est un artisan spécialisé dans le ferrage des chevaux ; il pose un fer sous chaque sabot du cheval afin de le protéger.
Mots-clés : premier principe de la thermodynamique, loi de Newton de la thermique
Le maréchal-ferrant est un artisan spécialisé dans le ferrage des chevaux ; il pose un fer sous chaque sabot du cheval afin de le protéger.
 |
Un fer à cheval doit être parfaitement adapté à la morphologie du sabot du cheval pour que celui-ci ne se blesse pas. Cela nécessite un ensemble d'opérations réalisées lors de la pose du fer par le maréchal-ferrant : le fer est chauffé à une température d'environ 900 °C dans une forge pour être malléable. À l'aide d'un marteau, il est ensuite déformé pour s'ajuster à la forme du sabot.
Données
• température du fer à la sortie de la forge : θ0 = 900 °C ;
• volume du fer à cheval : VFer = 104 cm3 ;
• masse volumique du fer, supposée indépendante de la température : ρFer = 7,87 g·cm−3 ;
• surface extérieure du fer à cheval : S = 293 cm2;
• température ambiante extérieure : θExt = 15 °C ;
• capacité thermique massique du fer supposée indépendante de la température :
cFer = 440 J·kg−1·K−1 ;
cFer = 440 J·kg−1·K−1 ;
• loi de Newton donnant l'expression du flux thermique reçu par le système {fer à cheval} de température θ en provenance de l'air extérieur, de température θExt :
Φ = h · S · (θExt − θ)
avec h le coefficient de transfert thermique surfacique et S la surface d'échange :
Φ = h · S · (θExt − θ)
avec h le coefficient de transfert thermique surfacique et S la surface d'échange :
- dans l'air : hair = 14 W·m−2·K−1 ;
- dans l'eau froide : heau = 360 W·m−2·K−1.
Partie 1. Chauffage du fer
Lors du chauffage du fer à cheval pour le rendre plus malléable, sa température passe de la température ambiante θExt = 15 °C à θ0 = 900 °C.
1. Déterminer la valeur de la masse mFer du fer à cheval.
Connaissant la masse volumique et le volume, on détermine la masse du fer à cheval.
2. Calculer la variation d'énergie interne ΔU du fer à cheval lors de cette étape.
La variation d'énergie interne est reliée à la variation de température subie par le fer à cheval.
3. Interpréter au niveau microscopique la variation d'énergie interne ΔU du fer à cheval.
Analysez le signe de la variation d'énergie interne calculée à la question précédente.
Partie 2. Refroidissement du fer
Lorsque le fer est à la température souhaitée de 900 °C, le maréchal-ferrant le sort de la forge et le façonne à l'aide d'un marteau pendant une minute environ. Il s'installe ensuite près du cheval et il s'écoule à nouveau environ une minute.
Le fer, encore chaud, est alors posé quelques secondes sur la face inférieure du sabot, ce qui est sans douleur pour l'animal, mais brûle la corne en laissant une trace. Cela permet au maréchal-ferrant de juger si la forme est satisfaisante. Si c'est le cas, il refroidit rapidement le fer en le trempant dans l'eau puis le fixe définitivement sur le sabot à l'aide de clous.
Le fer, encore chaud, est alors posé quelques secondes sur la face inférieure du sabot, ce qui est sans douleur pour l'animal, mais brûle la corne en laissant une trace. Cela permet au maréchal-ferrant de juger si la forme est satisfaisante. Si c'est le cas, il refroidit rapidement le fer en le trempant dans l'eau puis le fixe définitivement sur le sabot à l'aide de clous.
Partie 2.1. Refroidissement à l'air libre
On considère que les transferts thermiques entre le fer à cheval et le milieu extérieur suivent la loi de Newton. Le système étudié est le fer à cheval.
4. Le maréchal-ferrant martèle le fer à cheval dans l'air. Appliquer le premier principe de la thermodynamique pour le système étudié entre les instants t et t + Δt ; la durée Δt étant supposée faible devant une durée caractéristique d'évolution de la température et la température variant de θ(t) à θ(t + Δt).
En déduire que l'équation différentielle régissant l'évolution de la température du fer à cheval peut s'écrire sous la forme :
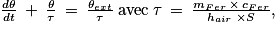
En déduire que l'équation différentielle régissant l'évolution de la température du fer à cheval peut s'écrire sous la forme :
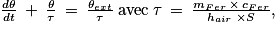
Comme le fer à cheval est au repos, son énergie mécanique ne varie pas. Il n'échange pas de travail avec l'extérieur, donc le premier principe de la thermodynamique se simplifie. Le calcul du flux thermique de deux manières différentes permettra d'en déduire l'équation différentielle.
Dans ces conditions τ = 880 s.
L'équation différentielle précédente admet pour solution la fonction :
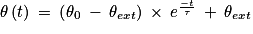
L'équation différentielle précédente admet pour solution la fonction :
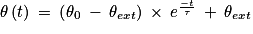
5. Vérifier que la fonction proposée θ(t) est bien la solution de l'équation différentielle précédente.
Remplacez la solution donnée dans l'équation différentielle de la question 4.
6. Calculer la valeur de la température du fer au moment où le maréchal-ferrant le pose sur la face inférieure du sabot du cheval. Commenter.
Calculez la température à la date de pose du fer à cheval.
Partie 2.2. Refroidissement dans l'eau avant la pose
Pour accélérer le refroidissement du fer afin de le poser rapidement sur le sabot, le maréchal-ferrant plonge le fer encore chaud à la température de 600 °C dans un récipient contenant de l'eau à température ambiante de 15 °C que l'on considère comme constante.
7. En adaptant la solution obtenue dans le cadre du modèle précédent, estimer la valeur de la durée nécessaire pour que le fer soit refroidi à une température θfinale = 40 °C à laquelle l'artisan pourra poser le fer à l'aide de clous sur le sabot du cheval.
Le candidat est invité à prendre des initiatives et à présenter la démarche suivie, même si elle n'a pas abouti. La démarche est évaluée et nécessite d'être correctement présentée.
Le candidat est invité à prendre des initiatives et à présenter la démarche suivie, même si elle n'a pas abouti. La démarche est évaluée et nécessite d'être correctement présentée.
Isolez le temps t dans la solution de l'équation différentielle donnée à la question 5.
8. Dans la réalité, 20 secondes suffisent pour refroidir le fer dans de l'eau à 15 °C. Commenter.
Déterminez les pertes possibles d'énergie.
Corrigé
1. On a la masse volumique et le volume du fer à cheval, d'où mFer = ρFer × VFer = 7,87 × 104 = 818 g
2. La variation d'énergie interne est ΔU = mFer × cFer × Δθ
D'où ΔU = 818 × 10−3 × 440 × (900 − 15) = 3,19 × 105J
D'où ΔU = 818 × 10−3 × 440 × (900 − 15) = 3,19 × 105J
3. L'énergie interne représente l'ensemble de toutes les énergies qui se manifestent à l'échelle microscopique. Elle est positive donc le fer à cheval gagne de la chaleur qui va se traduire par une augmentation de l'énergie cinétique microscopique des atomes (davantage d'agitation thermique).
4. Le système {fer à cheval} est au repos donc son énergie mécanique ne varie pas ; le premier principe de la thermodynamique donne ΔU = W + Q
Comme le système est incompressible (il n'échange pas de travail avec l'extérieur), Q = ΔU = mFer × cFer × Δθ
On a la loi de Newton :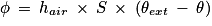
or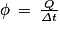
soit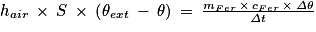
soit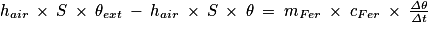
soit on divise par m × c :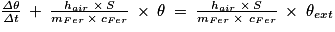
si on pose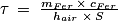 , on arrive à
, on arrive à 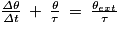
d'où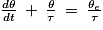
Comme le système est incompressible (il n'échange pas de travail avec l'extérieur), Q = ΔU = mFer × cFer × Δθ
On a la loi de Newton :
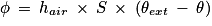
or
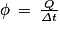
soit
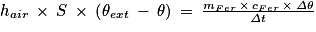
soit
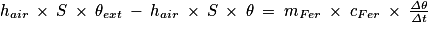
soit on divise par m × c :
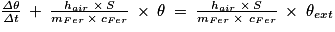
si on pose
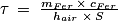 , on arrive à
, on arrive à 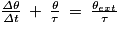
d'où
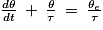
5. La solution proposée est : 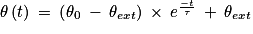
D'où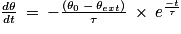
On remplace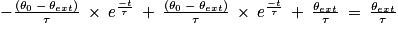
On obtient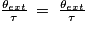 ce qui est toujours vrai
ce qui est toujours vrai
La solution proposée est la solution de l'équation différentielle.
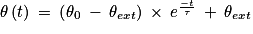
D'où
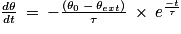
On remplace
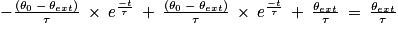
On obtient
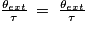 ce qui est toujours vrai
ce qui est toujours vraiLa solution proposée est la solution de l'équation différentielle.
6. Le maréchal-ferrant installe le fer à cheval au bout de 2 minutes,
soit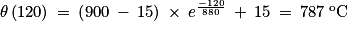
La corne du sabot du cheval se retrouve bien brûlée à une telle température.
soit
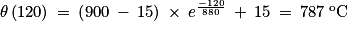
La corne du sabot du cheval se retrouve bien brûlée à une telle température.
7. On cherche à avoir une température finale de 40 °C.
Attention τ = 34,1 s puisqu'on est dans l'eau
Et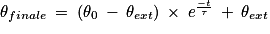
D'où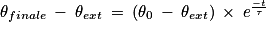
Soit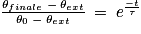
D'où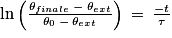
Soit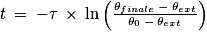
D'où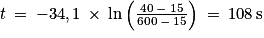
Attention τ = 34,1 s puisqu'on est dans l'eau
Et
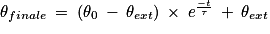
D'où
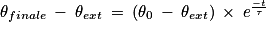
Soit
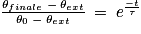
D'où
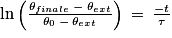
Soit
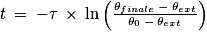
D'où
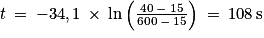
8. La solution utilisée pour modéliser le refroidissement ne s'applique pas ici, puisqu'on le plonge seulement 20 secondes. Il faut donc changer de modèle : en plongeant le fer à cheval dans l'eau, la température ne suit pas une équation linéaire du premier ordre, car il peut y avoir d'autres types d'échange entre le fer à cheval et l'eau comme le rayonnement par exemple. L'eau, au contact du fer à cheval à 600 °C, peut aussi localement changer d'état. La température de l'eau n'est peut-être pas constante.

