Étudier la dynamique d'un système électrique : le modèle du circuit Résistance-Condensateur (RC)
Énoncé
Exercice 1 (Nouvelle-Calédonie, 2008)
On étudie la décharge du condensateur de capacité C = 1,0 F à travers un conducteur ohmique de résistance R.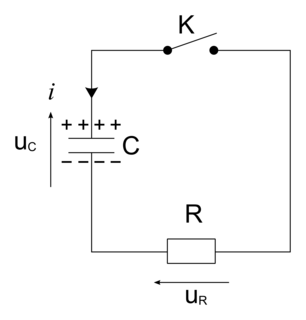 |
À t0 = 0 s, on ferme l'interrupteur K et la décharge débute. Initialement, la tension aux bornes du condensateur vaut U0 = 3,6 V.
1. Établir l'équation différentielle vérifiée par uc(t) pendant la décharge, et montrer qu'elle peut s'écrire sous la forme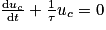 , où
, où 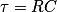 est la constante de temps du circuit.
est la constante de temps du circuit.
2. Montrer que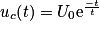 est solution de l'équation différentielle précédente.
est solution de l'équation différentielle précédente.
3. En déduire qu'une durée environ égale 5τ à permet une décharge quasi-complète du condensateur.
4. Si l'on considère que cette durée est égale à 20 min, déterminer la valeur de la résistance R du conducteur ohmique qu'il faut alors associer au condensateur de capacité C = 1,0 F.
1. Établir l'équation différentielle vérifiée par uc(t) pendant la décharge, et montrer qu'elle peut s'écrire sous la forme
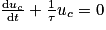 , où
, où 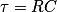 est la constante de temps du circuit.
est la constante de temps du circuit.2. Montrer que
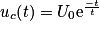 est solution de l'équation différentielle précédente.
est solution de l'équation différentielle précédente.3. En déduire qu'une durée environ égale 5τ à permet une décharge quasi-complète du condensateur.
4. Si l'on considère que cette durée est égale à 20 min, déterminer la valeur de la résistance R du conducteur ohmique qu'il faut alors associer au condensateur de capacité C = 1,0 F.
La bonne méthode
1. Appliquer la loi d'additivité des tensions (loi des mailles) sur le circuit et la loi d'Ohm, pour relier la tension aux bornes de la résistance au courant qui la traverse. Enfin, utiliser la relation entre le courant traversant un condensateur et sa tension.2. Injecter l'expression de uc dans l'équation différentielle établie précédemment.
3. Regarder combien vaut la tension à t = 5τ. Si elle est très petite par rapport à sa valeur initiale, on peut considérer la décharge du condensateur comme quasi-complète.
Exercice 2
Une partie de l'énergie solaire, abondante sur Terre, peut être transformée en énergie électrique par une cellule photovoltaïque (capteur solaire). Cette énergie électrique doit être stockée, car la demande énergétique peut être décalée dans le temps vis-à-vis de l'apport en énergie solaire (utilisation par exemple, d'un éclairage la nuit).
Dans cet exercice, on s'intéresse au stockage de l'énergie électrique dans un condensateur de grande capacité.
Le fabriquant du condensateur utilisé indique une valeur de capacité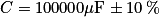 .
.
Les caractéristiques de la cellule photovoltaïque en régime normal de fonctionnement sont indiquées ci-dessous (toutes les données ne sont pas utiles) :
Puissance : 0,6 W
Intensité : 270 mA
Tension maximale : 2,25 V
Dimensions : 394 × 127 × 20 mm
Masse : 0,41 kg
Plage de température : −40 °C à +60 °C
La cellule photovoltaïque se comporte comme un générateur G débitant un courant d'intensité constante I = 0,27 A, tant que la tension à ses bornes reste inférieure à la tension maximaleUmax = 2,25 V.
La cellule photovoltaïque est branchée aux bornes du condensateur (figure 1).
Dans cet exercice, on s'intéresse au stockage de l'énergie électrique dans un condensateur de grande capacité.
Le fabriquant du condensateur utilisé indique une valeur de capacité
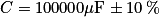 .
.Les caractéristiques de la cellule photovoltaïque en régime normal de fonctionnement sont indiquées ci-dessous (toutes les données ne sont pas utiles) :
Puissance : 0,6 W
Intensité : 270 mA
Tension maximale : 2,25 V
Dimensions : 394 × 127 × 20 mm
Masse : 0,41 kg
Plage de température : −40 °C à +60 °C
La cellule photovoltaïque se comporte comme un générateur G débitant un courant d'intensité constante I = 0,27 A, tant que la tension à ses bornes reste inférieure à la tension maximaleUmax = 2,25 V.
La cellule photovoltaïque est branchée aux bornes du condensateur (figure 1).
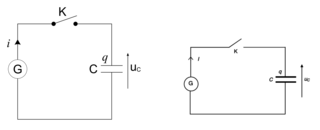 |
À la date t0 = 0 s, on ferme l'interrupteur K et on débute l'enregistrement informatisé des variations de la tension uc aux bornes du condensateur en fonction du temps. On obtient le graphe de la figure 2.
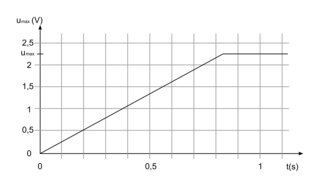 |
1. Nommer les deux régimes observables sur le graphe uc(t) = f(t) représenté en figure 2.
2. Donner l'expression de uc en fonction de C et de la charge q du condensateur.
3. Le condensateur est initialement déchargé. Donner l'expression de la charge q du condensateur en fonction de l'intensité I et du temps t lorsque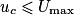 (charge à courant constant).
(charge à courant constant).
En déduire que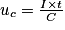 tant que
tant que 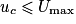 .
.
4. L'énergie électrique stockée dans le condensateur s'écrit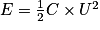 , avec U la tension à ses bornes. Calculer la quantité d'énergie électrique stockée dans le condensateur lorsque la charge est terminée.
, avec U la tension à ses bornes. Calculer la quantité d'énergie électrique stockée dans le condensateur lorsque la charge est terminée.
2. Donner l'expression de uc en fonction de C et de la charge q du condensateur.
3. Le condensateur est initialement déchargé. Donner l'expression de la charge q du condensateur en fonction de l'intensité I et du temps t lorsque
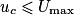 (charge à courant constant).
(charge à courant constant).En déduire que
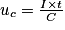 tant que
tant que 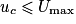 .
.4. L'énergie électrique stockée dans le condensateur s'écrit
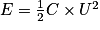 , avec U la tension à ses bornes. Calculer la quantité d'énergie électrique stockée dans le condensateur lorsque la charge est terminée.
, avec U la tension à ses bornes. Calculer la quantité d'énergie électrique stockée dans le condensateur lorsque la charge est terminée.La bonne méthode
1. Se souvenir des deux régimes régissant la charge (et la décharge) d'un condensateur, et faire le lien avec la figure.2. C'est une formule du cours.
3. Utiliser la relation entre I et le débit de charge
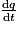 sachant que le courant est d'intensité constante à ce moment-là.
sachant que le courant est d'intensité constante à ce moment-là.4. Remarquer, sur la figure 2, que la tension aux bornes du condensateur atteint Umax lorsqu'il est chargé, puis appliquer la formule énoncée.
Corrigé
Exercice 1
1. On applique la loi d'additivité des tensions sur le circuit, soit uR + uc = 0. La loi d'Ohm nous donne uR = R × i. On a donc R×i + uc = 0.
Le courant i traversant le condensateur est relié à la tension à ses bornes par la relation :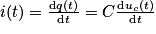 car
car 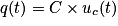 .
.
On a donc :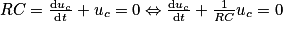 .
.
En posant τ = RC, on obtient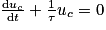 .
.
2. Soit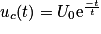 . Par dérivation, on a :
. Par dérivation, on a : 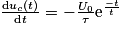 .
.
En remplaçant dans l'équation du 1., on obtient :
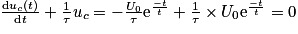 .
.
Donc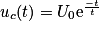 est bien solution de l'équation différentielle obtenue à la question 1.
est bien solution de l'équation différentielle obtenue à la question 1.
3. On calcule uc pour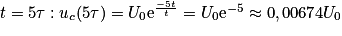 .
.
Au bout de t = 5τ, la tension uc aux bornes du condensateur vaut seulement 0,674 % de sa valeur initiale U0. On peut donc considérer sa décharge comme quasi-complète à ce moment-là.
4. On sait maintenant que 5τ = 20 × 60 = 1 200 s. Donc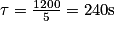 .
.
De plus, on a τ = RC, soit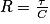 avec C = 1,0 F.
avec C = 1,0 F.
On en déduit donc que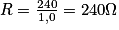 .
.
Le courant i traversant le condensateur est relié à la tension à ses bornes par la relation :
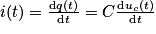 car
car 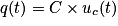 .
.On a donc :
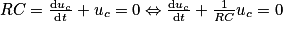 .
.En posant τ = RC, on obtient
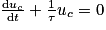 .
.2. Soit
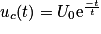 . Par dérivation, on a :
. Par dérivation, on a : 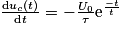 .
.En remplaçant dans l'équation du 1., on obtient :
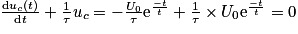 .
.Donc
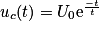 est bien solution de l'équation différentielle obtenue à la question 1.
est bien solution de l'équation différentielle obtenue à la question 1.3. On calcule uc pour
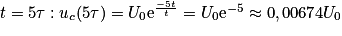 .
.Au bout de t = 5τ, la tension uc aux bornes du condensateur vaut seulement 0,674 % de sa valeur initiale U0. On peut donc considérer sa décharge comme quasi-complète à ce moment-là.
4. On sait maintenant que 5τ = 20 × 60 = 1 200 s. Donc
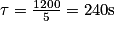 .
.De plus, on a τ = RC, soit
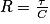 avec C = 1,0 F.
avec C = 1,0 F.On en déduit donc que
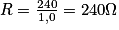 .
.Exercice 2
1. Jusqu'à 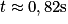 , la tension uc aux bornes du condensateur varie (proportionnellement) au temps : cela correspond au régime transitoire. Pour t > 0,82 s, la tension uc est constante : cela correspond au régime permanent.
, la tension uc aux bornes du condensateur varie (proportionnellement) au temps : cela correspond au régime transitoire. Pour t > 0,82 s, la tension uc est constante : cela correspond au régime permanent.
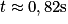 , la tension uc aux bornes du condensateur varie (proportionnellement) au temps : cela correspond au régime transitoire. Pour t > 0,82 s, la tension uc est constante : cela correspond au régime permanent.
, la tension uc aux bornes du condensateur varie (proportionnellement) au temps : cela correspond au régime transitoire. Pour t > 0,82 s, la tension uc est constante : cela correspond au régime permanent.2. Dans un condensateur, la formule qui lie la charge q et la tension à ses bornes est 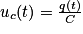 .
.
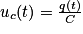 .
.3. La relation entre la charge d'un condensateur et le courant qui le traverse est : 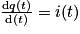 . Or d'après l'énoncé, le courant est constant, égal à I, tant que
. Or d'après l'énoncé, le courant est constant, égal à I, tant que 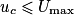 . On a donc
. On a donc 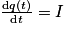 .
.
En effectuant un calcul de primitives, on obtient que q(t) = I × t + q(0).
Or le condensateur est déchargé initialement, on a donc q(0) = 0. D'où q(t) = I × t.
En remplaçant dans l'expression donnée à la question 2., on obtient :
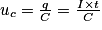 .
.
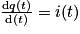 . Or d'après l'énoncé, le courant est constant, égal à I, tant que
. Or d'après l'énoncé, le courant est constant, égal à I, tant que 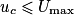 . On a donc
. On a donc 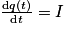 .
.En effectuant un calcul de primitives, on obtient que q(t) = I × t + q(0).
Or le condensateur est déchargé initialement, on a donc q(0) = 0. D'où q(t) = I × t.
En remplaçant dans l'expression donnée à la question 2., on obtient :
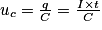 .
.4. On remarque, sur la figure 2, que la tension aux bornes du condensateur atteint Umax lorsqu'il est complètement chargé. De plus, d'après l'énoncé, on a C = 100 000 μF = 0,1 F.
En effectuant l'application numérique avec U = Umax = 2,25 V, on trouve l'énergie stockée par le condensateur lorsque celui-ci est chargé :
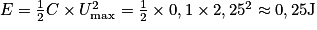 .
.
En effectuant l'application numérique avec U = Umax = 2,25 V, on trouve l'énergie stockée par le condensateur lorsque celui-ci est chargé :
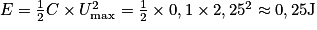 .
.
