Démontrer que deux droites sont parallèles à l'aide du théorème de Thalès
Problème
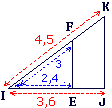 |
On donne un triangle IJK avec : IJ = 3,6 ; IK = 4,5.
On place E sur [IJ] et F sur [IK] tels que : IE = 2,4 et IF = 3.
On veut prouver que : (EF) // (KJ).
On place E sur [IJ] et F sur [IK] tels que : IE = 2,4 et IF = 3.
On veut prouver que : (EF) // (KJ).
Résolution
On va utiliser la réciproque du théorème de Thalès.
Par hypothèse, I, E, J, d'une part et I, F, K, d'autre part, sont alignés et ceci dans le même ordre.
On calcule que : 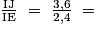 1,5 ;
1,5 ; 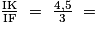 1,5
1,5
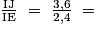 1,5 ;
1,5 ; 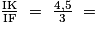 1,5
1,5Donc 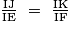 .
.
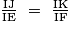 .
.Les deux hypothèses de la réciproque du théorème de Thalès étant vérifiées, on en déduit que : (EF) // (KJ).
Exercice n°1
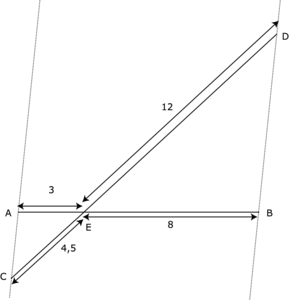
[AB] et [CD] sont deux segments sécants en E tels que AE = 3, EB = 8, CE = 4,5 et ED = 12. Fais une figure grandeur réelle.
Cochez la (ou les) bonne(s) réponse(s).
| ||
|
 |
• 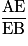 =
= 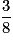 = 0,375.
= 0,375.
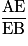 =
= 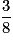 = 0,375.
= 0,375.• 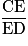 =
= 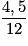 = 0,375.
= 0,375.
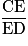 =
= 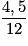 = 0,375.
= 0,375.Exercice n°2
Soit ABCD un quadrilatère. Les droites (AC) et (BD) se coupent en O. On a OA = 3,7 ; OC = 2,5 ; OB = 3 ; OD = 5. ABCD est-il un trapèze ?
Cochez la bonne réponse.
| ||
|
• Les rapports 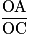 et
et 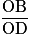 ne sont pas égaux donc (AB) et (DC) ne sont pas parallèles.
ne sont pas égaux donc (AB) et (DC) ne sont pas parallèles.
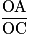 et
et 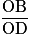 ne sont pas égaux donc (AB) et (DC) ne sont pas parallèles.
ne sont pas égaux donc (AB) et (DC) ne sont pas parallèles.• Les rapports 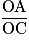 et
et 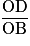 ne sont pas égaux donc (AD) et (BC) ne sont pas parallèles.
ne sont pas égaux donc (AD) et (BC) ne sont pas parallèles.
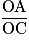 et
et 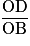 ne sont pas égaux donc (AD) et (BC) ne sont pas parallèles.
ne sont pas égaux donc (AD) et (BC) ne sont pas parallèles.Exercice n°3
Soit un triangle PQR tel que PQ = 6 cm et PR = 9 cm.
M est un point de [PQ] tel que : PM = 2 cm.
N est un point de [PR] tel que : PN = 6 cm.
M est un point de [PQ] tel que : PM = 2 cm.
N est un point de [PR] tel que : PN = 6 cm.
Fais une figure puis détermine la longueur PN pour que (MN) soit parallèle à (QR).
Écrivez la réponse dans la zone colorée.
PN = cm
• 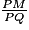 =
= 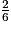 =
= 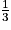 et
et 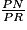 =
= 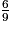 =
= 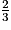
Les droites (MN) et (QR) ne sont donc pas parallèles.
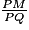 =
= 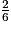 =
= 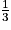 et
et 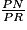 =
= 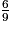 =
= 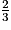
Les droites (MN) et (QR) ne sont donc pas parallèles.
• Pour que (MN) et (QR) soient parallèles, il faut que :
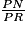 =
= 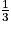 donc PN =
donc PN = 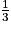 PR = 3
PR = 3
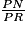 =
= 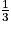 donc PN =
donc PN = 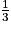 PR = 3
PR = 3
