La physique du jonglage, sujet de métropole, mai 2022, exercice au choix A
Énoncé
Exercice sur 5 points
Mots-clés : mouvement dans un champ de pesanteur uniforme, énergie mécanique
L'art du jonglage est la plus ancienne des disciplines de cirque connues ; son origine remonte à l'Égypte ancienne. Le but de cet exercice est d'étudier le mouvement d'une balle lors d'une démonstration filmée.
On étudie, dans le référentiel terrestre supposé galiléen, le mouvement d'une balle de jonglage de masse m et de centre de masse C.
L'art du jonglage est la plus ancienne des disciplines de cirque connues ; son origine remonte à l'Égypte ancienne. Le but de cet exercice est d'étudier le mouvement d'une balle lors d'une démonstration filmée.
On étudie, dans le référentiel terrestre supposé galiléen, le mouvement d'une balle de jonglage de masse m et de centre de masse C.
Données :
• intensité de la pesanteur : g = 9,81 m · s−2.
La figure 1 est extraite d'une vidéo au cours de laquelle une personne jongle avec plusieurs balles. On suit le mouvement dune balle.
Dans cette étude :
Dans cette étude :
- on note (x ; y) les coordonnées de la position de C dans le repère (O ; x ; y) et (vx ; vy) celles de sa vitesse ;
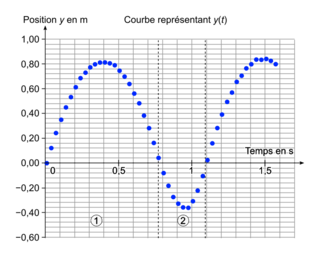
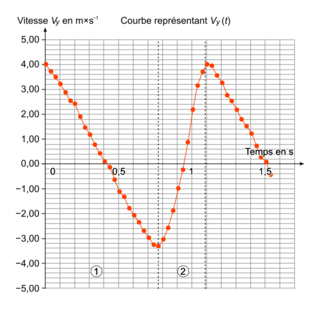
- les évolutions temporelles y(t) et vy(t) sont respectivement représentées sur les figures 2a et 2b qui font apparaître alternativement des phases notées 1 et 2 ;
- à la date t = 0 s la balle, située à l'origine du repère, quitte pour la première fois la main du jongleur avec une vitesse initiale
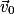 ;
; - lorsque la balle n'est pas en contact avec la main du jongleur, elle est enchute libre. Elle effectue alors un mouvement parabolique en passant d'une main à l'autre, la réception et le lancer se faisant toujours en y = 0 m ;
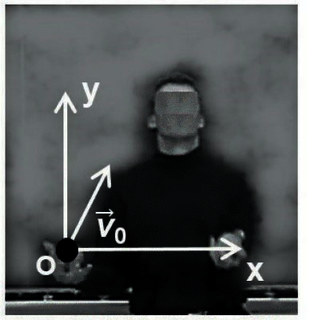 |
Figure 1. Photographie
– la référence de l'énergie potentielle de pesanteur est choisie à l'ordonnée y = 0 m.
– la référence de l'énergie potentielle de pesanteur est choisie à l'ordonnée y = 0 m.
 |
 |
1. Décrire qualitativement, selon l'axe Oy, le mouvement de la balle lors de la phase 1; à l'aide des figures 2a et 2b.
Observez le mouvement de la balle selon l'axe Oy. En mettant en correspondance la courbe représentant la vitesse de la balle, on pourra décrire au mieux la phase 1.
2. Interpréter la figure 2a pour décrire le rôle de la main sur le mouvement de la balle lors de la phase 2.
Procédez de la même manière pour la phase 2. Déterminez le mouvement où la balle arrive dans la main et quitte de nouveau la main.
3. Justifier à l'aide de la deuxième loi de Newton, dans le cadre du modèle de la chute libre, que la valeur de la composante vx de la vitesse est constante et égale à la vitesse initiale v0x lorsque la balle n'est plus en contact avec la main du jongleur.
La balle est en chute libre, elle n'est donc soumise qu'à son poids, qui est une force verticale. Déterminez les composantes du vecteur accélération puis celles du vecteur vitesse.
4. Exprimer l'énergie mécanique initiale Em0 de la balle en fonction de sa masse m et des composantes v0x et v0y de la vitesse initiale dans le référentiel terrestre.
L'énergie mécanique est la somme de l'énergie cinétique de la balle et de l'énergie potentielle de la balle.
5. Dans toute la suite de l'exercice, on ne s'intéresse qu'à la phase 1. À l'aide d'un raisonnement énergétique appliqué lors de la phase 1, établir que l'expression de l'altitude maximale H atteinte par la balle s'écrit :
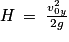
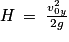
Déterminez l'expression de l'énergie mécanique au sommet de la trajectoire de la balle. Comme les frottements sont négligeables, l'énergie mécanique se conserve.
6. Déterminer la valeur de H à partir de la relation précédente et d'une lecture graphique de v0y sur la figure 2b. Comparer le résultat à celui obtenu par lecture graphique de la figure 2a.
La figure 2b donne la valeur de v0y.
7. Établir l'expression littérale de la coordonnée vy(t) du vecteur vitesse de la balle lors de la phase 1.
La question 3 permet de déterminer la coordonnée du vecteur vitesse selon Oy.
8. Évaluer l'intensité de la pesanteur g à l'aide de la figure 2b lors de la phase 1. Commenter.
Le coefficient directeur de la droite modélisant la courbe de vy(t) donne, au signe près, l'intensité de la pesanteur g.
9. Déterminer l'équation horaire y(t) du mouvement du centre de la balle lors de la phase 1.
La primitive de la coordonnée de la vitesse vy(t) donne l'équation horaire y(t).
10. On note tair la durée pendant laquelle la balle est en l'air lors de la phase 1. Établir l'expression de tair en fonction de v0y et de g. En déduire que l'expression du temps de vol dans l'air d'une balle s'écrit :
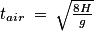
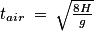
La vitesse v0y est déduite de l'expression trouvée à la question 5. La balle est en l'air tant que la valeur y(t) est positive.
11. Calculer la valeur de tair en utilisant la valeur de H obtenue par lecture graphique de la figure 2a. Commenter.
Faites l'application numérique et commentez la valeur obtenue.
Corrigé
1.
Phase 1 :
• de t0 = 0 s à t1 = 0,4 s, la balle s'élève de 0,0 m jusqu'à 0,82 m. Sa vitesse, en valeur absolue, diminue jusqu'à s'annuler ;
• puis de t1 = 0,4 s à t2 = 0,75 s, la balle redescend jusqu'à 0,0 m. Et sa vitesse augmente en valeur absolue.
2. Dans la phase 2 : le jongleur attrape la balle en l'accompagnant de t2 = 0,75 s à t3 = 0,95 s. Dès qu'il a attrapé la balle, le vecteur vitesse change de sens et il la renvoie vers le haut en lui communiquant une vitesse initiale entre à t3 = 0,95 s et à t4 = 1,1 s, date à laquelle la balle quitte la main.
3. Lors d'une chute libre, la balle n'est soumise qu'à son poids 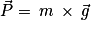 qui est vertical vers le haut. Comme la deuxième loi de Newton donne :
qui est vertical vers le haut. Comme la deuxième loi de Newton donne :
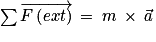 et que la seule force qui s'applique ne dépend que de l'axe Oy.
et que la seule force qui s'applique ne dépend que de l'axe Oy.
Le vecteur accélération aura donc pour composante selon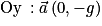 ;
;
Le vecteur vitesse sera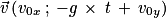 avec le vecteur vitesse initiale
avec le vecteur vitesse initiale 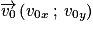 .
.
La composante de la vitesse ne dépend donc que de v0x qui est une constante.
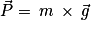 qui est vertical vers le haut. Comme la deuxième loi de Newton donne :
qui est vertical vers le haut. Comme la deuxième loi de Newton donne :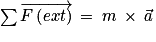 et que la seule force qui s'applique ne dépend que de l'axe Oy.
et que la seule force qui s'applique ne dépend que de l'axe Oy.Le vecteur accélération aura donc pour composante selon
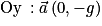 ;
;Le vecteur vitesse sera
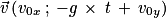 avec le vecteur vitesse initiale
avec le vecteur vitesse initiale 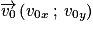 .
.La composante de la vitesse ne dépend donc que de v0x qui est une constante.
4. 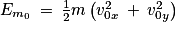
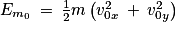
5. Au point le plus haut, la vitesse, selon l'axe Oy, est nulle et l'énergie mécanique vaut 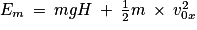 .
.
Or, si on considère que les frottements sont négligeables, l'énergie mécanique se conserve, c'est-à-dire que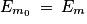
Soit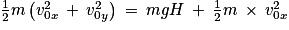
Soit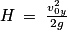
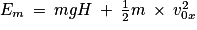 .
.Or, si on considère que les frottements sont négligeables, l'énergie mécanique se conserve, c'est-à-dire que
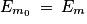
Soit
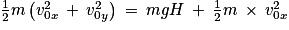
Soit
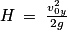
6. Graphiquement sur la figure 2b, on trouve v0y = 4,00 m/s
D'où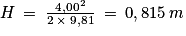 , ce qui est en concordance avec la figure 2a qui donne 0,82 m environ également.
, ce qui est en concordance avec la figure 2a qui donne 0,82 m environ également.
D'où
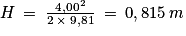 , ce qui est en concordance avec la figure 2a qui donne 0,82 m environ également.
, ce qui est en concordance avec la figure 2a qui donne 0,82 m environ également.7. D'après la question 3 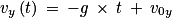
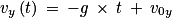
8. Entre 0,00 s et 0,76 s environ, le graphe vy(t) est assimilable une droite décroissante dont le coefficient directeur est égal à l'opposé de l'intensité de la pesanteur soit −g. Comme v0y = 4,00 m/s et que vy(0,4) = 0 m/s.
Soit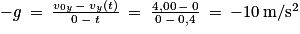 donc g = 10 m/s2
donc g = 10 m/s2
La valeur est proche, compte tenu des incertitudes de lecture de la vraie valeur.
Soit
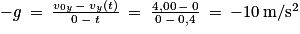 donc g = 10 m/s2
donc g = 10 m/s2La valeur est proche, compte tenu des incertitudes de lecture de la vraie valeur.
9. On a vy(t) = −g × t + v0y
D'où y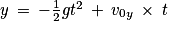
D'où y
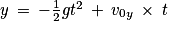
10. La balle est en l'air tant qu'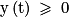 . On cherche le temps de vol tair tel qu'y(t) = 0
. On cherche le temps de vol tair tel qu'y(t) = 0
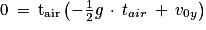
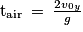
or d'après la question 5 :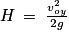
soit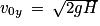
on remplace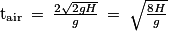
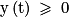 . On cherche le temps de vol tair tel qu'y(t) = 0
. On cherche le temps de vol tair tel qu'y(t) = 0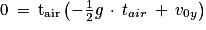
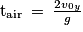
or d'après la question 5 :
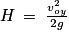
soit
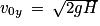
on remplace
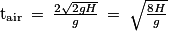
11. On trouve 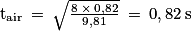
C'est extrêmement rapide d'où le fait d'être un très bon jongleur.
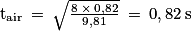
C'est extrêmement rapide d'où le fait d'être un très bon jongleur.

